next up previous contents index
Next: Bibliografia Up: Twierdzenie Mengera Previous: Twierdzenie Mengera   Spis rzeczy   Indeks

Ćwiczenia

Ćwiczenie 8.1   Napisz problem prymalny i dualny dla znajdowania maksymalnego przepływu w sieci przedstawionej na poniższym rysunku (dla dowolnej funkcji przepustowości $c:A \rightarrow {\bf R}$).
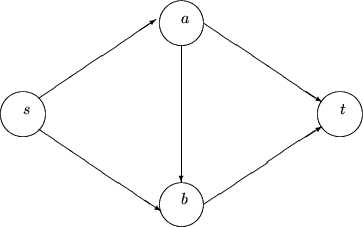
\begin{picture}(90,60) \put(10,30){\circle{10}} \put(10,30){$s$} \put(80,30)... ...}} \put(50,50){\vector(3,-2){26}} \put(45,45){\vector(0,-1){30}} \end{picture}

Ćwiczenie 8.2   Metodą Forda-Fulkersona znajdź maksymalny przepływ i minimalny przekrój w poniższej sieci.

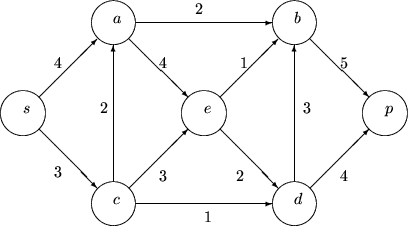
\begin{picture}(100,55) \put(10,30){\circle{10}} \put(10,30){$s$} \put(17,40)... ...ctor(1,-1){12.94}} \put(90,30){\circle{10}} \put(90,30){$p$} \end{picture}

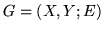
Ćwiczenie 8.3   Skorzystaj z algorytmu Forda-Fulkersona by znaleźć maksymalne skojarzenie w grafie dwudzielnym $G=(X,Y;E)$, gdzie:
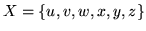
$X=\{ u,v,w,x,y,z\}$
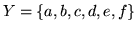
$Y=\{ a,b,c,d,e,f\}$
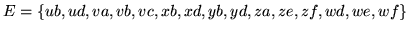
$E=\{ ub, ud, va, vb, vc, xb, xd, yb, yd, za, ze, zf, wd, we, wf\}$
Skomentuj otrzymany wynik.

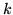
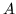
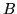
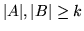
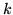
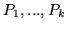
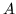
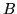
Ćwiczenie 8.4   Wykaż, że jeśli graf jest $k$ spójny to dla dowolnych rozłącznych zbiorów wierzchołków $A$ i $B$ takich, że $\vert A\vert, \vert B\vert \geq k$ istnieje $k$ ścieżek $P_1,...,P_k$ o rozłącznych zbiorach wierzchołków takich, że początkowy wierzchołek każdej ze ścieżek jest w zbiorze $A$ a końcowy w $B$.