MATEMATYKA

Liczby zespolone - zadania 3

1) Rozwiąż równanie w zbiorze liczb zespolonych:
.

2) Rozwiąż w zbiorze liczb zespolonych równania:

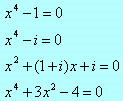
3) W równaniu kwadratowym, gdy wyróżnik jest mniejszy od zera, otrzymujemy dwa różne zespolone pierwiastki kwadratowe z wyróżnika. W takiej sytuacji po podstawieniu do wzoru na x₁ dwóch różnych pierwiastków z wyróżnika i analogicznie do wzoru na x₂, dostaniemy cztery pierwiastki. A równocześnie wiemy, że równanie kwadratowe ma dokładnie dwa rozwiązania w zbiorze liczb zespolonych. Jak to można wytłumaczyć?

Jeżeli popełniałeś błędy albo miałeś trudności, naciśnij przycisk 'Utrwalenie'.
Natomiast jeżeli wszystko zrozumiałeś i te zadania nie sprawiły Ci trudności, to naciśnij przycisk 'OK'.