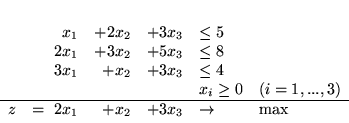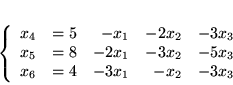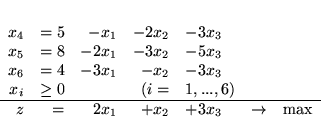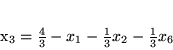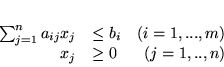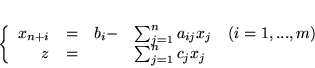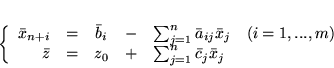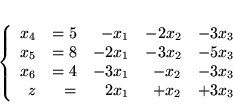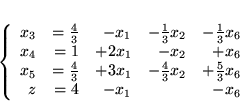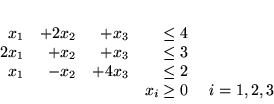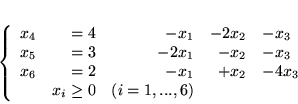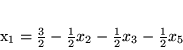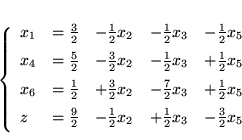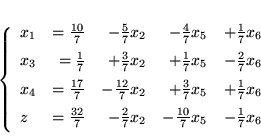Jak to działa? Chwytamy byka za rogi

Metodą wykładu będzie chwytanie byka za rogi. Podobnie jak to zrobił w swojej książce Vašek Chvátal [4], rozpoczniemy nie od prezentacji ogólnej metody, a od pokazania na przykładach jak ona dziala. W ten sposób, gdy przyjdzie czas na pełne przedstawienie metody, będziemy rozumieli o czym mówimy - sytuacja która w matematyce nie zdarza się zbyt często.

Przykład 3.1   Rozważmy PPL:

$$\begin{array}{rrrrll} &x_1 & + 2x_2 & +3x_3 & \leq 5\\ ... ...e z & = \ 2x_1&+x_2&+3x_3 & \rightarrow & \max \end{array}$$ (3.1)

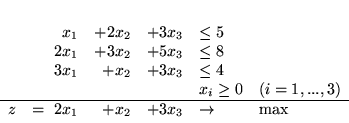Pierwszym krokiem będzie wprowadzenie zmiennych dodatkowych 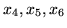$x_4, x_5, x_6$, które zdefiniujemy następująco:

$$\left\{ \begin{array}{rrrrr} x_4 & = 5 & - x_1 & -2x_2 ... ...\\ x_6 & = 4 & - 3x_1 & - x_2 & -3x_3 \end{array} \right.$$ (3.2)

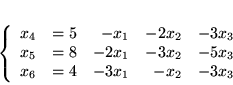Rozważmy teraz problem następujący

$$\begin{array}{rrrrlll} x_4 & = 5 & - x_1 & -2x_2 & -3x_3\... ...z & = & 2x_1 & +x_2 & +3x_3 & \rightarrow & \max \end{array}$$ (3.3)

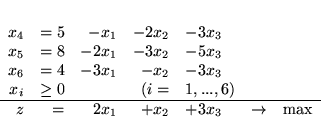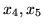
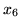
Jest zupełnie oczywistym, że problemy () i () są równoważne w tym sensie, że każde rozwiązanie optymalne problemu () daje nam pewne rozwiązanie optymalne problemu () (wystarczy wartości zmiennych $x_4,x_5$ i $x_6$ wyznaczyć z równości ()). Podobnie, każde optymalne rozwiązanie problemu () dostarcza nam optymalnego rozwiązania ().
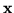
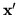
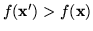
Metoda będzie polegała na tym, że mając pewne rozwiązanie dopuszczalne problemu () ${\bf x}$, będziemy szukali następnego rozwiązania ${\bf x'}$ takiego, że $f({\bf x'}) > f({\bf x})$, a więc lepszego. Takie postępowanie będziemy powtarzali wielokrotnie, otrzymując rozwiązania coraz bliższe optymalnego (o ile takie istnieje).
O pierwsze rozwiązanie dopuszczalne w naszym przykładzie nietrudno. Połóżmy

$$x_1=x_2=x_3=0.$$

Wtedy oczywiście

$$x_4=5, \ \ x_5 = 8, \ \ x_6=4, \ \ z=0.$$

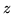
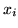
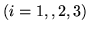
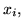
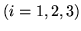
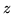
Przyjrzyjmy się teraz wzorowi na $z$ w (). Ponieważ współczynniki przy $x_i$ $(i=1,,2,3)$ są dodatnie, jeśli zwiększymy wartość którejkolwiek ze zmiennych $x_i,$ $(i=1,2,3)$, wtedy zwiększy się także wartość $z$. Wartość ta będzie się tym szybciej powiększać, im jest większy współczynnik (dodatni) przy powiększanym iksie we wzorze na $z$.
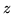
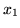
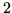
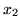
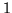
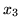
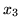
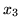
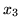
Współczynnikiem przy $x_1$ jest $2$, przy $x_2$ $1$, natomiast przy $x_3$ $3$. Będziemy więc zwiększać wartość $x_3$. O ile można powiększyć $x_3$ bez zmieniania wartości pozostałych zmiennych, by otrzymane w ten sposób nowe rozwiązanie było dopuszczalne? Wartość $x_3$ można zwiększyć o tyle, by zostały zachowane w dalszym ciągu nierówności

$$x_4 \geq 0, \ \ \ x_5 \geq 0, \ \ \ x_6 \geq 0$$

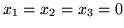
(pamiętamy, że w naszym rozwiązaniu $x_1 = x_2 =x_3 =0$). Łatwo zauważyć, że

$$x_4 \geq 0 \Rightarrow x_3 \leq \frac{5}{3}, \ \ \ x_5 \geq 0... ...frac{8}{5}, \ \ \ x_6 \geq 0 \Rightarrow x_3 \leq \frac{4}{3}.$$

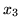
Największą wartością $x_3$ jaką możemy wybrać jest oczywiście

$$x_3 = \frac{4}{3}$$

Wtedy oczywiście

$$z = 4$$

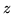
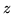
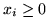
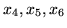
Zauważmy jak oczywista jest tu metoda postępowania. Funkcja celu wyraża się przy pomocy zmiennych które w naszym rozwiązaniu dopuszczalnym miały początkową wartość równą zero. Jasne więc było, że jeśli zwiększyć wartość tej zmiennej która we wzorze na $z$ ma współczynnik dodatni, zwiększy się także wartość $z$. Z kolei ograniczenia $x_i \geq 0$ i wzory na $x_4, x_5, x_6$ pozwaliły z łatwością ustalić o ile wolno nam zwiększyć wartości poszczególnych zmiennych tak, by otrzymać rozwiązanie dopuszczalne.
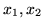
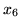
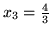
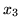
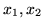
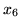
Teraz wartość zero przyjmują zmienne $x_1, x_2$ oraz $x_6$, natomiast $x_3=\frac{4}{3}$. Przedstawmy $x_3$ przy pomocy $x_1, x_2$ i $x_6$ korzystając z trzeciego z równań ()

$$x_3=\frac{4}{3} - x_1 - \frac{1}{3}x_2 -\frac{1}{3}x_6$$ (3.4)

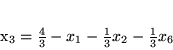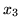
Tak otrzymane $x_3$ wstawmy do wzoru na $z$:

$$z=4-x_1-\frac{1}{2}x_6$$

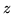
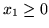
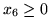
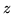
Wobec warunków $x_1\geq 0$ i $x_6 \geq 0$ jest oczywiste, że maksymalną wartością jaką może przyjąć $z$ jest 4. Rozwiązanie:

$$x_1=0, \ \ x_2=0, \ \ x_3 = \frac{4}{3}, \ \ z=4$$

jest rozwiązaniem optymalnym.$\Box$

To co zrobiliśmy w przykładzie spróbujmy teraz przenieść na przypadek ogólny. Niech będzie dany PPL

$$\begin{array}{rlr} \sum^{n}_{j=1} a_{ij}x_j & \leq b_i & (i=1,...,m)\\ x_j & \geq 0 & (j=1,..,n) \end{array}$$ (3.5)

$\ z \ = \ \sum^{n}_{j=1} c_{j}x_j \ \ \rightarrow \ \ \mbox{max}$

Problem ten jest oczywiście równoważny problemowi znalezienia maksymalnej wartości $z$ spełniającej układ równań:

$$\left\{ \begin{array}{rclll} x_{n+i} & = & b_i - & \sum^... ......,m)\\ z & = & & \sum^n_{j=1}c_jx_j \end{array} \right.$$ (3.6)

przy założeniu, że $x_l \geq 0$, dla $l=1,...,n+m$. Podobnie jak to miało miejsce w przykładzie (), także w przypadku ogólnym będziemy rozważali układ równań

$$\left\{ \begin{array}{rcclll} \bar{x}_{n+i} & = & \bar{b... ..._0 & + & \sum^n_{j=1}\bar{c}_j\bar{x}_j \end{array} \right.$$ (3.7)

skojarzony z PPL () równoważny układowi w tym sensie, że otrzymany z niego przez, być może wielokrotne, zamiany ról zmiennych znajdujących się po prawej i lewej stronie układu.

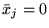
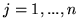
Definicja 3.1   Układ równań () nazywamy słownikiem PPL (). Słownik () nazywamy słownikiem dopuszczalnym PPL (), jeżeli po podstawieniu $\bar{x}_j=0$ dla $j=1,...,n$, otrzymamy rozwiązanie dopuszczalne (inaczej mówiąc, jeżeli

$$\bar{x}_1=...=\bar{x}_n=0; \ \ \bar{x}_{n+1}=\bar{b}_1,...,\bar{x}_{n+m}=\bar{b}_m$$ (3.8)

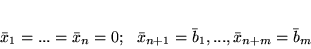jest rozwiązaniem dopuszczalnym PPL ()).
Zmienne po lewej stronie znaków równości w słowniku nazywamy zmiennymi bazowymi, zmienne po prawej stronie niebazowymi.

Zwróćmy uwagę, że dla słownika () wektor ${\bf\bar{x}}=(\bar{x}_1,...,\bar{x}_{n+m})$ zdefiniowany wzorem () nie musi być rozwiązaniem dopuszczalnym PPL (). Źeby ${\bf\bar{x}}$ był rozwiązaniem dopuszczalnym wszystkie liczby $\bar{b}_1,...,\bar{b}_m$ muszą być nieujemne, a to wcale nie musi zachodzić. Stąd następna definicja.

Definicja 3.2   Wektor $(\bar{x}_k)_{k=1,...,n+m}$ dany równaniami () nazywamy rozwiązaniem bazowym.

W przykładzie mieliśmy do czynienia z dwoma słownikami:

$$\left\{ \begin{array}{rrrrr} x_4 & = 5 & - x_1 & -2x_2 ... ...& -3x_3 \\ z&= &2x_1 & + x_2 &+3x_3 \end{array} \right.$$ (3.9)

oraz

$$\left\{ \begin{array}{rrrrr} x_3 & = \frac{4}{3} & - x_... ...c{5}{3}x_6 \\ z&= 4 & - x_1 & & - x_6 \end{array} \right.$$ (3.10)

(Słownika () nie mieliśmy potrzeby wypisywać wcześniej. Źeby go otrzymać należy $x_3$ ze wzoru () wstawić do wzorów na $z, x_4$ i $x_5$ w słowniku ().)
W słowniku () zmiennymi bazowymi są $x_4,x_5$ i $x_6$, zaś $x_1,x_2,x_3$ są zmiennymi niebazowymi. W () zmienne bazowe to $x_3,x_4,x_5$, zmienne niebazowe $x_1,x_2,x_6$.
Oba słowniki są dopuszczalne bo, dla przykładu, rozwiązanie bazowe () $x_1=x_2=x_6=0$, $x_3=\frac{4}{3}, \ x_4=1, \ x_5=\frac{4}{3}$, jest równocześnie rozwiązaniem dopuszczalnym ($x_i \geq 0$ dla $i=1,...,6)$).
W przykładzie wystarczyła jedna iteracja do otrzymania rozwiązania optymalnego. W następnym przykładzie zobaczymy, że tak być nie musi. Opis tego przykładu ułatwią nam nowe definicje.

Przykład 3.2   Rozwiążemy PPL:

$$\begin{array}{rrrrl} x_1 & + 2x_2 & +x_3 & \leq 4\\ 2x_... ... 4x_3 & \leq 2\\ &&&x_i \geq 0 & \ i=1,2,3 \end{array} \\$$ (3.11)

$z \ = \ 3x_1 \ + \ x_2 \ + \ 2x_3 \ \rightarrow \ \mbox{max}$

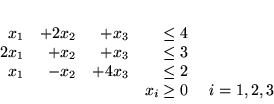Zdefiniujmy zmienne dodatkowe (są one równocześnie zmiennymi bazowymi pierwszego słownika).

$$\left\{ \begin{array}{rrrrl} x_4 & = 4 & - x_1 & - 2x_2 ... ... & - 4x_3\\ &x_i \geq 0 & (i=1,...,6) \end{array} \right.$$ (3.12)

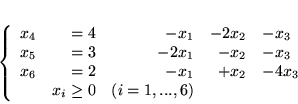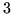
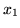
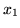
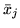
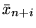
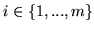
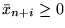
Największym współczynnikiem dodatnim w funkcji celu jest $3$ (współczynnik przy $x_1$), stąd nową zmienną bazową będzie $x_1$. Taką zmienną $\bar{x}_j$ będziemy nazywali zmienną wchodzącą. Zmienną wychodzącą, czyli taką która przestanie w następnym kroku być zmienną bazową, jest $\bar{x}_{n+i}$ ( $i \in \{1,...,m\}$) dla którego nierówność $\bar{x}_{n+i} \geq 0$ daje najostrzejsze ograniczenie od góry na wartość zmiennej wchodzącej. 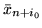Inaczej mówiąc, $\bar{x}_{n+i_{0}}$ jest zmienną wychodzącą słownika () jeżeli

$$\frac{\bar{b}_{i_{0}}}{\bar{a}_{i_{0}j}} \geq 0 \mbox{\ \ \ i... ...e \frac{\bar{b}_i}{\bar{a}_{ij}} \geq 0, \ i=1,...,m\right\}$$

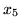
W naszym przykładzie zmienną wychodzącą będzie $x_5$, łatwo bowiem sprawdzić, że

$x_4\geq 0 \Rightarrow x_1 \leq 4$

$x_5 \geq 0 \Rightarrow x_1 \leq \frac{3}{2}$

$x_6 \geq 0 \Rightarrow x_1 \leq 2$.

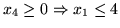
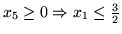
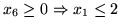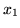
Obliczamy więc $x_1$ z drugiego równania słownika ()

$$x_1 = \frac{3}{2} - \frac{1}{2}x_2 - \frac{1}{2}x_3 - \frac{1}{2}x_5$$ (3.13)

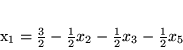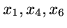
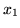
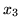
i tworzymy nowy słownik o zmiennych bazowych $x_1, x_4, x_6$ przepisując () jako pierwsze równanie i tworząc pozostałe dwa z pierwszego i trzeciego równań słownika (), zastępując w nich $x_1$ prawą stroną wzoru (). Nową funkcję celu otrzymamy wstawiając $x_3$ dane wzorem () do starej funkcji celu. W rezultacie otrzymamy słownik dopuszczalny:

$$\left\{ \begin{array}{lrrrl}\vspace{0.2cm} x_1 & = \frac... ..._2 & + \frac{1}{2}x_3 & -\frac{3}{2}x_5 \end{array} \right.$$ (3.14)

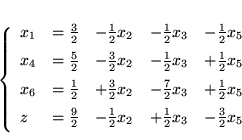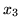
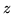
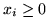
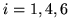
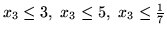
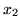
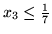
Teraz jako zmienną wchodzącą musimy wybrać $x_3$ ponieważ tylko ta zmienna ma współczynnik dodatni we wzorze na $z$. Nierówności $x_i \geq 0$ dla $i=1,4,6$ dają, odpowiednio, nierówności dla wchodzącej zmiennej bazowej: $x_3 \leq 3, \ x_3 \leq 5, \ x_3 \leq \frac{1}{7}$. 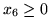Z tych nierówności najostrzejszym ograniczeniem na wartość $x_2$ od góry jest jest $x_3 \leq \frac{1}{7}$, otrzymana z $x_6 \geq 0$, tak więc wychodzącą zmiennbazowjest $x_{6}$. 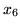Po analogicznych do poprzednich obliczeniach, otrzymamy nowy słownik (już trzeci dla naszego problemu):

$$\left\{ \begin{array}{lrrrl}\vspace{0.2cm} x_1 & = \frac... ...2 & - \frac{10}{7}x_5 & -\frac{1}{7}x_6 \end{array} \right.$$ (3.15)

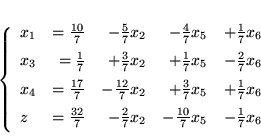Ten słownik jest już ostatnim. Jest dopuszczalny, a jego rozwiązanie bazowe

$$x_1= \frac{10}{7},\ x_2=0,\ x_3=\frac{1}{7},\ x_4=\frac{17}{7},\ x_5=x_6=0,\ z=\frac{32}{7}$$

jest rozwiazaniem optymalnym. $\Box$