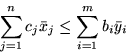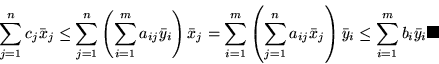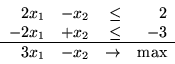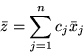Next: Korzyści
Up: Dualizm
Previous: Dualizm
Spis rzeczy
Indeks
Problem dualny programowania liniowego
Definicja 4.1
Niech będzie dany PPL
|
(4.1) |
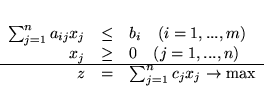 |
PPL
|
(4.2) |
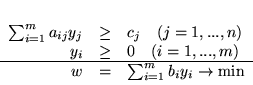 |
nazywamy
problemem dualnym problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
).
Problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy
problemem prymalnym.
Z łatwością można się przekonać, że po sprowadzeniu problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) do postaci
standardowej otrzymamy PPL którego problemem dualnym jest wyjściowy PPL (
) do postaci
standardowej otrzymamy PPL którego problemem dualnym jest wyjściowy PPL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
Tak więc prawdziwy jest natychmiast następujący wniosek.
).
Tak więc prawdziwy jest natychmiast następujący wniosek.
Wniosek 4.1
Problemem dualnym do problemu dualnego do PPL jest wyjściowy PPL.
Przykład 4.1
Problemem dualnym do
|
(4.3) |
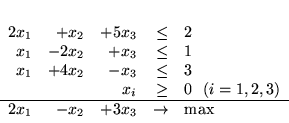 |
jest
|
(4.4) |
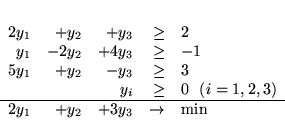 |
Następne twierdzenie bywa nazywane słabą zasadą dualności.
Twierdzenie 4.2
Niech (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) będzie problemem prymalnym a (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) problemem do niego dualnym.
Jeżeli
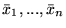
oraz
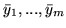
są
rozwiązaniami dopuszczalnymi, odpowiednio, problemów (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) i
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) to
Dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) jest wyjątkowo prosty i mieści się
w jednej linijce:
jest wyjątkowo prosty i mieści się
w jednej linijce:
Przykład 4.1 (c.d.)
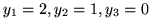
jest rozwiązaniem dopuszczalnym (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) o wartości
funkcji celu
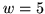
. Stąd i z twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
wynikają dwa wnioski:
- problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest ograniczony,
) jest ograniczony,
- wartość maksymalna funkcji celu jest co najwyżej równa
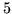 .
.
Oczywisty jest następujący wniosek z twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) .
.
Wniosek 4.3
Jeżeli problem prymalny jest nieograniczony, to problem do niego dualny
jest sprzeczny.
Przykład 4.2
Może się zdarzyć, że oba problemy: prymalny i dualny są sprzeczne.
Tak jest na przykład dla problemu prymalnego:
Z twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika, że gdyby udało nam się znaleźć takie rozwiązanie dopuszczalne
wynika, że gdyby udało nam się znaleźć takie rozwiązanie dopuszczalne
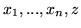 problemu prymalnego (
problemu prymalnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
i
)
i 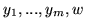 problemu do niego dualnego (
problemu do niego dualnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), że
), że 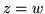 , to
każde z tych rozwiązań byłoby rozwiązaniem optymalnym swojego
problemu. Powstaje pytanie: kiedy takie rozwiązania istnieją? Zaraz
zobaczymy, że zawsze wtedy gdy problemy (
, to
każde z tych rozwiązań byłoby rozwiązaniem optymalnym swojego
problemu. Powstaje pytanie: kiedy takie rozwiązania istnieją? Zaraz
zobaczymy, że zawsze wtedy gdy problemy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są
niesprzeczne. Mówi o tym twierdzenie sformułowane w ostatecznej
formie przez D. Gale'a, H.W. Kuhna i A.W. Tuckera w 1951 roku.
) są
niesprzeczne. Mówi o tym twierdzenie sformułowane w ostatecznej
formie przez D. Gale'a, H.W. Kuhna i A.W. Tuckera w 1951 roku.
Twierdzenie 4.4 (Zasada dualności.)
Jeżeli zagadnienie prymalne (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma rozwiązanie optymalne
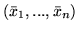
to problem dualny (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma także
rozwiązanie optymalne
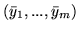
i zachodzi równość
|
(4.5) |
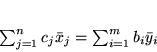 |
Dowód. Przypuśćmy, że
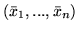 jest optymalnym
rozwiązaniem problemu prymalnego (
jest optymalnym
rozwiązaniem problemu prymalnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Zgodnie z twierdzeniem
). Zgodnie z twierdzeniem ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wystarczy wskazać
takie rozwiązanie
wystarczy wskazać
takie rozwiązanie
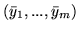 problemu dualnego (
problemu dualnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), żeby
zachodziła równość (
), żeby
zachodziła równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Przypuśćmy, że ostatnim słownikiem otrzymanym dla problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
jest słownik w którym funkcja celu wyraża się wzorem
)
jest słownik w którym funkcja celu wyraża się wzorem
|
(4.6) |
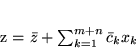 |
Pamiętamy, że we wzorze (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
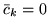 gdy
gdy 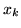 jest zmienną niebazową ostatniego słownika
jest zmienną niebazową ostatniego słownika
-
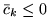 dla każdego
dla każdego 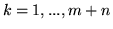 , bowiem zakładamy, że (
, bowiem zakładamy, że (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma rozwiązanie optymalne.
) ma rozwiązanie optymalne.
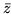 jest oczywiście wartością maksymalną funkcji celu problemu (
jest oczywiście wartością maksymalną funkcji celu problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i, skoro
) i, skoro
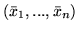 jest rozwiązaniem optymalnym, zachodzi
jest rozwiązaniem optymalnym, zachodzi
Wykażemy, że szukanym rozwiązaniem optymalnym problemu dualnego jest
W tym celu przepiszemy wzór (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) po dokonaniu na nim
następujących manipulacji:
) po dokonaniu na nim
następujących manipulacji:
- -
- zastępujemy
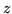 przez
przez
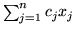 ,
,
- -
- korzystając z faktu, że
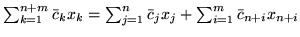 (
(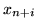 są zmiennymi sztucznymi), zastępujemy
są zmiennymi sztucznymi), zastępujemy
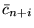 przez
przez 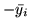 (inaczej mówiąc, definiujemy
(inaczej mówiąc, definiujemy
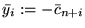 )
)
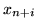 przez
przez
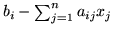 .
.
Otrzymamy wtedy wzór
a stąd po łatwych przekształceniach
|
(4.7) |
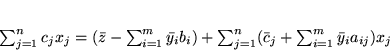 |
Równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest równością wielomianów zmiennych
) jest równością wielomianów zmiennych
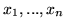 , stąd
, stąd
|
(4.8) |
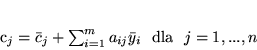 |
oraz
|
(4.9) |
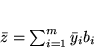 |
Równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oznacza, że zachodzi równość (
) oznacza, że zachodzi równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
Ponieważ
).
Ponieważ
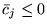 dla wszystkich
dla wszystkich 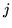 , równość
(
, równość
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) pociąga
) pociąga
a więc
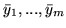 jest rozwiązaniem dopuszczalnym
problemu (
jest rozwiązaniem dopuszczalnym
problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i twierdzenie zostało wykazane.
Wzajemne zależności pomiędzy problemem prymalnym a dualnym
wygodnie będzie mieć zapisane w poniższej tabeli.
) i twierdzenie zostało wykazane.
Wzajemne zależności pomiędzy problemem prymalnym a dualnym
wygodnie będzie mieć zapisane w poniższej tabeli.
| Jeśli problem prymalny |
to problem dualny |
| ma rozwiązanie optymalne |
ma rozwiązanie optymalne o tej |
| skończone |
samej wartości (twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ) |
| jest nieograniczony |
jest sprzeczny (wniosek ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ) |
| jest sprzeczny |
jest sprzeczny lub nieograniczony |





Next: Korzyści
Up: Dualizm
Previous: Dualizm
Spis rzeczy
Indeks