




Next: Sieci
Up: Grafy i sieci
Previous: Macierz incydencji
Spis rzeczy
Indeks
Ścieżką o długości 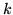 w grafie
w grafie 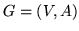 nazywamy
ciąg wierzchołków
nazywamy
ciąg wierzchołków
i łuków
|
(8.1) |
 |
takich, że 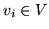 dla
dla 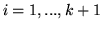 ,
, 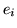 jest łukiem o końcach
jest łukiem o końcach 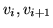 dla
dla 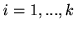 , oraz
, oraz 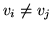 dla
dla 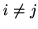 .
.
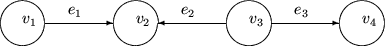
Rys. 8.2
O łuku
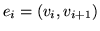 mówimy, że jest zgodny ze ścieżką
mówimy, że jest zgodny ze ścieżką 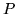 , zaś
jeśli
, zaś
jeśli
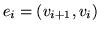 mówimy, że
mówimy, że 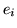 jest niezgodny z
jest niezgodny z 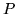 .
.
Na rysunku 8.2 łuki 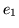 i
i 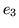 są zgodne, zaś łuk
są zgodne, zaś łuk 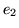 niezgodny ze ścieżką
niezgodny ze ścieżką
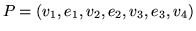 , o łukach
, o łukach
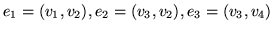 .
.
Jeśli, dodatkowo, założymy, że 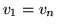 (przy zachowaniu
(przy zachowaniu 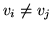 dla wszystkich
pozostałych przypadków), to ścieżkę (
dla wszystkich
pozostałych przypadków), to ścieżkę (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) nazywamy cyklem.
) nazywamy cyklem.