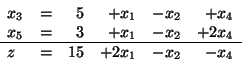Next: Cykliczność
Up: Szczegóły metody
Previous: Ćwiczenia
Contents
Działanie algorytmu polega na wykonywaniu następujących kroków:
- Wybór zmiennej bazowej wchodzącej.
Przypomnijmy, że nową zmienną wchodzącą jest zmienna
 taka, że
taka, że
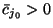 . Jeśli jest więcej niż jedna taka zmienna, można, jak to robiliśmy w przykładach, wybrać tę dla której dodatnie
. Jeśli jest więcej niż jedna taka zmienna, można, jak to robiliśmy w przykładach, wybrać tę dla której dodatnie 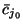 jest największe (z nadzieją - ale bez gwarancji - że taki wybór nas najszybciej doprowadzi do celu).
jest największe (z nadzieją - ale bez gwarancji - że taki wybór nas najszybciej doprowadzi do celu).
Jeśi taki wybór jest niemożliwy to wszystkie współczynniki 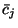 dla
dla 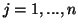 we wzorze
we wzorze
są ujemne. To zaś oznacza, że rozwiązanie dopuszczalne stowarzyszone ze słownikiem dopuszczalnym jest optymalne (w szczególności maksymalna wartość 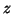 jest równa
jest równa 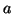 ).
).
- Wybór zmiennej wychodzącej.
Jako zmienną wychodzącą przyjmujemy tę która daje najostrzejsze ograniczenie od góry na zmienną wchodzącą  .
.
Na przykład, dla słownika dopuszczalnego
zmienną wchodzącą jest 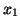 . Nierówności
. Nierówności 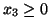 i
i  dają dla
odpowiedniego rozwiązania dopuszczczalnego (tj. takiego w którym
dają dla
odpowiedniego rozwiązania dopuszczczalnego (tj. takiego w którym 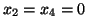 )
ograniczenia następujące:
)
ograniczenia następujące:
Wybieramy zmienną wychodzącą 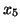 .
.
Jeśli na wartości zmiennej wchodzącej nie otrzymujemy ograniczenia od góry,
jak w przykładzie słownika
czyli jeśli współczynniki przy  są nieujemne, to wartość
są nieujemne, to wartość 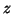 jest
oczywiście nieograniczona od góry. Nie ma rozwiązania maksymalnego,
jest
oczywiście nieograniczona od góry. Nie ma rozwiązania maksymalnego, 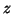 może być
dowolnie duże.
może być
dowolnie duże.
- Tworzenie nowego słownika
W tym kroku algorytmu tworzymy nowy słownik przy pomocy prostych operacji arytmetycznych.
Ostatecznie na pytanie czy simpleks może się zaciąć? postawione w tytule
niniejszego ustępu odpowiedź brzmi nie. Nie w tym sensie,
że w każdym momencie swojego działanie algorytm albo poda rozwiązanie
problemu (tzn rozwiązanie optymalne lub
informację, że problem jest sprzeczny lub nieograniczony), albo
będzie wykonywał następne
kroki. Czy to oznacza, że wszystko musi się dobrze skończyć? Zobaczymy zaraz, że
niekoniecznie.




Next: Cykliczność
Up: Szczegóły metody
Previous: Ćwiczenia
Contents