



Next: Ćwiczenie (przykład Chvatála)
Up: Szczegóły metody
Previous: Czy simpleks może się
Contents
Zacznijmy od przykładu.
Przykład 3.4
Rozważmy słownik
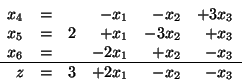 |
(3.25) |
Rozwiązaniem bazowym tego słownika jest
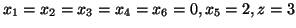
.
Zmienną wchodzącą będzie
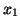
, zaś zmienną wychodzącą może być
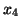
lub

. Wybierzmy na przykład
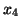
. Nowym słownikiem będzie:
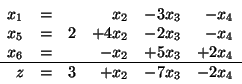 |
(3.26) |
Zauważmy więc, że na naszej operacji zamiany słownika nic nie zyskaliśmy
w tym sensie, że wartość
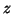
nie wzrosła.
Sytuacja w której zastąpienie jednej ze zmiennych bazowych zmienną niebazową
według podanych przez nas reguł nie spowoduje zwiększenia wartości
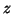 w rozwiązaniu bazowym może zajść tylko wtedy, gdy wartość jednej ze
zmiennych w rozwiązaniu bazowym wynosi zero. W naszym przykładzie takimi zmiennymi
były
w rozwiązaniu bazowym może zajść tylko wtedy, gdy wartość jednej ze
zmiennych w rozwiązaniu bazowym wynosi zero. W naszym przykładzie takimi zmiennymi
były 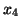 i
i  dla słownika (
dla słownika (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i
) i 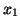 i
i  dla słownika (
dla słownika (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Definicja 3.3
Mówimy, że rozwiązanie bazowe słownika jest zdegenerowane jeżeli co
najmniej jedna zmienna bazowa w tym rozwiązaniu przyjmuje wartość zero.
Odpowiedni słownik także nazywamy zdegenerowanym.
Przykład 3.4 (cd)
Czytelnik zechce sprawdzić, że następnym (po (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)) słownikiem
będzie
a więc simpleks doprowadził do rozwiązania optymalnego PPl (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
),
rozwiązaniem
optymalnym jest
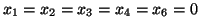
,
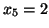
,
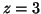
.
Ponieważ przy przejściu ze słownika (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) do (
) do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) rozwiązanie nie polepszyło się
(wartość
) rozwiązanie nie polepszyło się
(wartość 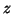 w tych słownikach jest taka sama)
powstaje pytanie, czy może zaistnieć sytuacja w której po kilku zmianach
słownika algorytm wróci do słownika który był już rozważany?
w tych słownikach jest taka sama)
powstaje pytanie, czy może zaistnieć sytuacja w której po kilku zmianach
słownika algorytm wróci do słownika który był już rozważany?
Odpowiedź na to pytanie brzmi tak! Jest jasne, że jeśli konsekwentnie według
jakiejś reguły wybieramy zmienne wchodzące i wychodzące i na jeden i ten sam
słownik wpadamy dwa razy, wtedy algorytm będzie już gonił w piętkę,
te same słowniki będą sie pojawiały cyklicznie.
Zauważmy od razu, że taka sytuacja może się pojawić tylko wtedy gdy pojawi się
słownik zdegenerowany - jeśli nie, to w każdej iteracji rozwiązanie bazowe jest
inne, różni się od wszystkich poprzednich wartością 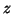 chociażby.
chociażby.
W przykładzie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) oba słowniki (
oba słowniki (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są zdegenerowane.
Czytelnik zechce sprawdzić, że przykład Chvátala [3] zaproponowany poniżej
jako ćwiczenie jest problemem PL w którym po kilku odpowiednio
przeprowadzonych iteracjach wracamy do wyjściowego słownika 3.3.
) są zdegenerowane.
Czytelnik zechce sprawdzić, że przykład Chvátala [3] zaproponowany poniżej
jako ćwiczenie jest problemem PL w którym po kilku odpowiednio
przeprowadzonych iteracjach wracamy do wyjściowego słownika 3.3.
Z twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika w szczególności, że każde rozwiązanie bazowe
jest rozwiązaniem każdego innego słownika (nie tylko tego którego jest
rozwiązaniem bazowym). Stąd zaś,
że wszystkich możliwych rozwiązań bazowych dla PPL jest
tyle na ile sposobów można wybrać
wynika w szczególności, że każde rozwiązanie bazowe
jest rozwiązaniem każdego innego słownika (nie tylko tego którego jest
rozwiązaniem bazowym). Stąd zaś,
że wszystkich możliwych rozwiązań bazowych dla PPL jest
tyle na ile sposobów można wybrać 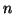 elementów (zmiennych bazowych)
spośród
elementów (zmiennych bazowych)
spośród 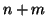 elementów (tyle jest wszystkich zmiennych), a więc
elementów (tyle jest wszystkich zmiennych), a więc
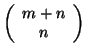 .
Tak więc słowników dla danego PPL jest skończona liczba
.
Tak więc słowników dla danego PPL jest skończona liczba
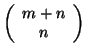 i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
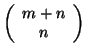 ).
Wykazaliśmy więc
twierdzenie:
).
Wykazaliśmy więc
twierdzenie:
Twierdzenie 3.2
Jeśli algorytm simpleks nie goni w piętkę
3.4, to rozwiązuje PPL w skończonej
liczbie iteracji. Co więcej, jeśli problem jest
niesprzeczny i ograniczony, to istnieje rozwiązanie bazowe które jest równocześnie rozwiązaniem optymalnym.
Subsections




Next: Ćwiczenie (przykład Chvatála)
Up: Szczegóły metody
Previous: Czy simpleks może się
Contents
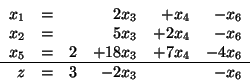
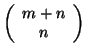 .
Tak więc słowników dla danego PPL jest skończona liczba
.
Tak więc słowników dla danego PPL jest skończona liczba
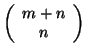 i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
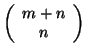 ).
Wykazaliśmy więc
twierdzenie:
).
Wykazaliśmy więc
twierdzenie: