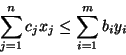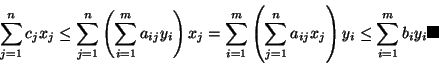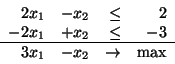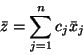Next: Korzyści
Up: Dualizm
Previous: Dualizm
Contents
Definicja 4.1
Niech będzie dany PPL
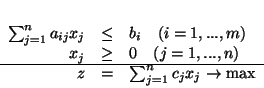 |
(4.1) |
PPL
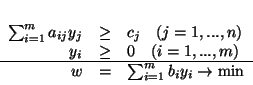 |
(4.2) |
nazywamy
problemem dualnym problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
). Problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy
problemem prymalnym. Równocześnie problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy problemem
dualnym problemu (prymalnego) (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
).
Z powyższej definicji wynika natychmiast następujący wniosek.
Wniosek 4.1
Problemem dualnym do problemu dualnego do PPL jest wyjściowy PPL.
Przykład 4.1
Problemem dualnym do
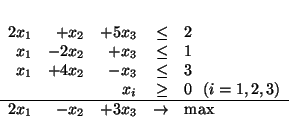 |
(4.3) |
jest
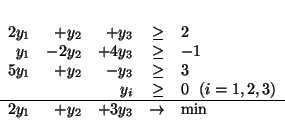 |
(4.4) |
Twierdzenie 4.1
Niech (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) będzie problemem prymalnym a (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) problemem do niego dualnym. Jeżeli
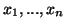
oraz

są
rozwiązaniami dopuszczalnymi, odpowiednio, problemów (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) i
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) to
Dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) jest wyjątkowo prosty i mieści się
w jednej linijce:
jest wyjątkowo prosty i mieści się
w jednej linijce:
Przykład 4.1 (c.d.)
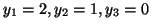
jest rozwiązaniem dopuszczalnym (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) o wartości funkcji celu
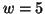
. Stąd i z twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
wynikają dwa wnioski:
- problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest ograniczony,
) jest ograniczony,
- wartość maksymalna funkcji celu jest co najwyżej równa
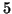 .
.
Zasada którą widzieliśmy w przykładzie działa także w ogólności.
Wniosek 4.2
Jeżeli problem prymalny jest nieograniczony, to problem do niego dualny
jest sprzeczny.
Przykład 4.2
Może się zdarzyć, że oba problemy: prymalny i dualny są sprzeczne.
Tak jest na przykład dla problemu prymalnego:
Z twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika, że gdyby udało nam się znaleźć takie rozwiązanie dopuszczalne
wynika, że gdyby udało nam się znaleźć takie rozwiązanie dopuszczalne 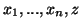 problemu prymalnego (
problemu prymalnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
i
)
i 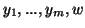 problemu do niego dualnego (
problemu do niego dualnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), że
), że 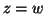 , to
każde z tych rozwiązań byłoby rozwiązaniem optymalnym swojego
problemu. Powstaje pytanie: kiedy takie rozwiązania istnieją? Zaraz
zobaczymy, że zawsze wtedy gdy problemy (
, to
każde z tych rozwiązań byłoby rozwiązaniem optymalnym swojego
problemu. Powstaje pytanie: kiedy takie rozwiązania istnieją? Zaraz
zobaczymy, że zawsze wtedy gdy problemy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są
niesprzeczne. Mówi o tym twierdzenie sformułowane w ostatecznej
formie przez D. Gale'a, H.W. Kuhna i A.W. Tuckera w 1951 roku.
) są
niesprzeczne. Mówi o tym twierdzenie sformułowane w ostatecznej
formie przez D. Gale'a, H.W. Kuhna i A.W. Tuckera w 1951 roku.
Twierdzenie 4.2 (Zasada dualności.)
Jeżeli zagadnienie prymalne (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma rozwiązanie optymalne
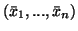
to problem dualny (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma także
rozwiązanie optymalne
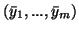
i zachodzi równość
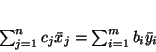 |
(4.5) |
Dowód. Przypuśćmy, że
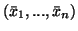 jest
rozwiązaniem problemu prymalnego (
jest
rozwiązaniem problemu prymalnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Zgodnie z twierdzeniem
). Zgodnie z twierdzeniem ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wystarczy wskazać takie rozwiązanie
wystarczy wskazać takie rozwiązanie
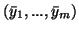 problemu dualnego (
problemu dualnego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), żeby
zachodziła równość (
), żeby
zachodziła równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Przypuśćmy, że ostatnim słownikiem otrzymanym dla problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
jest słownik w którym funkcja celu wyraża się wzorem
)
jest słownik w którym funkcja celu wyraża się wzorem
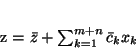 |
(4.6) |
Pamiętamy, że we wzorze (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
- -
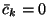 gdy
gdy 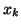 jest zmienną niebazową ostatniego słownika
jest zmienną niebazową ostatniego słownika
- -
-
 dla każdego
dla każdego 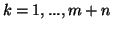 , bowiem zakładamy, że (
, bowiem zakładamy, że (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma rozwiązanie optymalne.
) ma rozwiązanie optymalne.
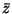 jest oczywiście wartością maksymalną funkcji celu problemu (
jest oczywiście wartością maksymalną funkcji celu problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i, skoro
) i, skoro
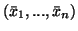 jest rozwiązaniem optymalnym, zachodzi
jest rozwiązaniem optymalnym, zachodzi
Wykażemy, że szukanym rozwiązaniem optymalnym problemu dualnego jest
W tym celu przepiszemy wzór (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) po dokonaniu na nim
następujących manipulacji:
) po dokonaniu na nim
następujących manipulacji:
- -
- zastępujemy
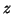 przez
przez
 ,
,
- -
- korzystając z faktu, że
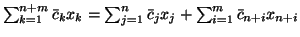 (
(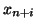 są zmiennymi sztucznymi), zastępujemy
są zmiennymi sztucznymi), zastępujemy
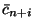 przez
przez 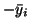 (inaczej mówiąc, definiujemy
(inaczej mówiąc, definiujemy
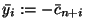 )
)
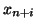 przez
przez
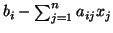 .
.
Otrzymamy wtedy wzór
a stąd połatwych przekształceniach
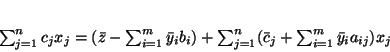 |
(4.7) |
Równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest równością wielomianów zmiennych
) jest równością wielomianów zmiennych
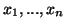 , stąd
, stąd
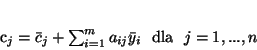 |
(4.8) |
oraz
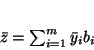 |
(4.9) |
Równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oznacza, że zachodzi równość (
) oznacza, że zachodzi równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
Ponieważ
).
Ponieważ
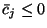 dla wszystkich
dla wszystkich 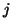 , równość
(
, równość
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) pociąga
) pociąga
a więc
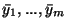 jest rozwiązaniem dopuszczalnym
problemu (
jest rozwiązaniem dopuszczalnym
problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i twierdzenie zostało wykazane.
) i twierdzenie zostało wykazane.




Next: Korzyści
Up: Dualizm
Previous: Dualizm
Contents