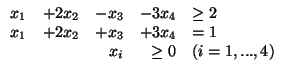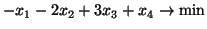Next: Niezbędne definicje
Up: Ogólny problem programowania liniowego
Previous: Ogólny problem programowania liniowego
Contents
- Sprowadź poniższe problemy programowania liniowego do postaci standardowej:
- (a)
- zmaksymalizować:
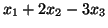
- przy warunkach:
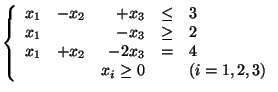
- (b)
- zminimalizować:
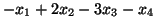
- przy warunkach:
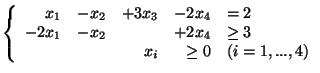 .
.
- (c)
-
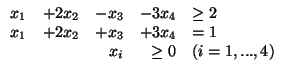
- Problem diety.
To bardzo znany, klasyczny wręcz problem. Przedstawmy go w bardzo
wielkim uproszczeniu - pełne dane do potraktowania problemu zupełnie
serio można znaleźć w [19].
Ola postanowiła odżywiać się najtaniej jak to możliwe, dostarczając jednak swojemu organizmowi odpowiednich ilości białka, witamin A i C, wapnia oraz energii. Postanowiła odżywiać sie mlekiem, serem, chlebem,
cielęciną i marchewką. Oto zawartości odpowiednich składników w tych produktach (na 100 g produktu).
| |
mleko |
ser |
chleb |
cielęcina |
marchew |
| białko (g) |
3 |
38 |
0 |
20 |
1 |
| wit A (jedn.) |
140 |
120 |
0 |
0 |
5760 |
| wit C (mg) |
1 |
0 |
0 |
0 |
3 |
| wapń (mg) |
120 |
1450 |
90 |
8 |
19 |
| energia (kcal) |
53 |
200 |
240 |
82 |
21 |
Zapotrzebowania dobowe Oli na poszczególne składniki podajemy w poniższej tabeli.
| białko |
70 |
| wit A |
5000 |
| wit C |
75 |
| wapń |
70 |
| energia |
2700 |
Ceny produktów:
| mleko |
1,5 zł/l |
| ser |
5zł/kg |
| chleb |
1,5 zł/kg |
| cielęcina |
12 zł/kg |
| marchew |
0,8 zł/kg |
Ułóż PPL po którego rozwiązaniu Ola będzie wiedziała jak
za najniższą możliwie cenę zaspokoi potrzeby swojego organizmu.
Waga dziennego pożywienia nie może przekroczyć 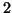 kg2.1.
kg2.1.




Next: Niezbędne definicje
Up: Ogólny problem programowania liniowego
Previous: Ogólny problem programowania liniowego
Contents
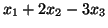
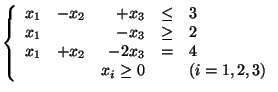
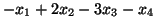
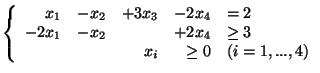 .
.