- ... studiorum1.1
- Powtarzanie jest matką uczenia się
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matematycznego1.2
- Warto zauważyć i zapamiętać tę definicję, szczególnie wobec faktu, że słowo programowanie występuje w bardzo różnym od rozważanego znaczeniu w bliskiej matematyce informatyce.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kg2.1
-
To po to by nasza Ola nie musiała jeść wyłącznie marchewki z chlebem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... często3.1
- Bierze się to z pewnością stad, że nie wszystko jest tak proste jak PL.
Zawsze jednak można próbować odstraszyć co bardziej niecierpliwych czytelników.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... jeżeli3.2
- niezły przykład na to, jak można skomplikować rzeczy proste:
wystarczy formalizacja matematyczna...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... słownika3.3
- Można wykazać,
że PPL w którym występuje zjawisko cykliczności musi mieć co najmniej 7 zmiennych
decyzyjnych. Przykład Chvátala jest więc, w pewnym sensie najmniejszym PPL który
goni w piętkę.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... piętkę3.4
- Inaczej: jeśli nie
występuje zjawisko cykliczności.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elegancją3.5
- elegancja (mat.) = prostota (wulg.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...błędną3.6
- Tu błędna
nie pochodzi od słowa błąd a raczej od
błędnego rycerza lub błędnego ognika.
Taka co to raz jest a raz jej nie ma - w
ogóle nie wie czego chce.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zmiennych3.7
- Sprawdź sam jeśli nie wierzysz - za najbardziej wiarygodne
i efektowne rozwiązanie będzie nagroda - pewno skromna, ale do odbioru w sensownym czasie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... następująco3.8
- Wyjątkowo w tym przypadku, wygodniej nam będzie oznaczać zmienne sztuczne przez
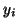 zamiast, jak to było zawsze do tej pory, przez
zamiast, jak to było zawsze do tej pory, przez 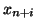 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... niewiadomymi4.1
-
Pamiętamy z dowodu twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , że w najgorszym przypadku iteracji może być
, że w najgorszym przypadku iteracji może być
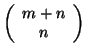 w pierwszym i
w pierwszym i
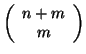 drugim przypadku, a więc tyle samo
drugim przypadku, a więc tyle samo
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fizycznych4.2
- W tym fragmencie tekstu słowo jednostka
występuje w dwóch zupełnie różnych znaczeniach.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)5.1
- Nigdy nie obliczamy
 przez wyliczenie macierzy
przez wyliczenie macierzy 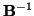 co jest wysiłkiem dużym i zupełnie zbędnym. Szczególnie wtedy,
gdybyśmy chcieli w tym celu wykorzystać zupełnie nieefektywną metodę
wyznacznikową.
co jest wysiłkiem dużym i zupełnie zbędnym. Szczególnie wtedy,
gdybyśmy chcieli w tym celu wykorzystać zupełnie nieefektywną metodę
wyznacznikową.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ma)6.1
- Jeżeli dolne ograniczenia są skończone, to można zmienne
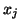 zastąpić nowymi zmiennymi
zastąpić nowymi zmiennymi 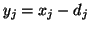 i przyjąć standardowe ograniczenia
i przyjąć standardowe ograniczenia 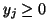 (por. Gass [8]). Ograniczenia od góry na poszczególne zmienne w praktyce występują prawie zawsze. Na przykład, jeśli zmienne
(por. Gass [8]). Ograniczenia od góry na poszczególne zmienne w praktyce występują prawie zawsze. Na przykład, jeśli zmienne 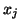 oznaczają wielkość produktów
oznaczają wielkość produktów  ,
, 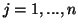 , to górne ograniczenia mogą oznaczać popyt na odpowiednie produkty.
, to górne ograniczenia mogą oznaczać popyt na odpowiednie produkty.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ogra\-ni\-cze\-niom6.2
- W metodzie sympleks z któr obcujemy od trzeciego rozdziału przyjmujemy wartość
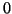 dla zmiennych niebazowych, a więc także wartość indywidualnego ograniczenia (dolnego, innego nie bylo) na zmienne.
dla zmiennych niebazowych, a więc także wartość indywidualnego ograniczenia (dolnego, innego nie bylo) na zmienne.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... są6.3
- właściwie mogą być
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
beznadziejny8.1
- Jeszcze raz podkreślmy, co znaczy to teoretycznie: sympleks jest
algorytmem niewielomianowym jak wykazuje przykład Klee-Minty'ego, w praktycznych zaś przykładach spisuje się bardzo dobrze.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interpretacji8.2
- Jak i samo
szukanie życiowego partnera przy pomocy programowania liniowego lub grafów. Choć podobno u Inków...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nazywamy8.3
- Niekonsekwentnie...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
łuków8.4
- Na przykład gdy będziemy myśleli o sieciach wodociągowych, kanalizacyjnych
- ale także, czasami, drogowych.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... łuków8.5
- Na przykład dla sieci
komunikacyjnej.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... łuków8.6
- W sieci komunikacyjnej: gdy myślimy raczej o cenie biletu niż odległości.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... łukach8.7
- W praktyce oznacza to, że woda nie płynie jak nie ma rury.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... powiększająca8.8
- Dokładniej ścieżka powiększająca (z którą zetknęliśmy się już w dowodzie twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) to ścieżka z
) to ścieżka z 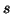 do
do 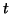 - właśnie przeszliśmy po niej pod prąd.
- właśnie przeszliśmy po niej pod prąd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... senacie8.9
- Także Senacie Akademii Górniczo-Hutniczej.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... problemami8.10
- W Senacie AGH są to Komisje Dydaktyczna, Naukowa, Budżetowa i inne.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
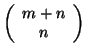 w pierwszym i
w pierwszym i
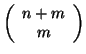 drugim przypadku, a więc tyle samo
drugim przypadku, a więc tyle samo