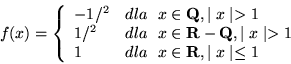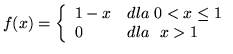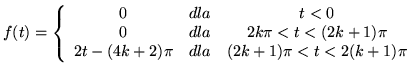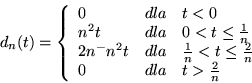Next: Bibliografia
Up: Zadania z matematyki dla
Previous: Szeregi Fouriera
Contents
- Wykaż, że funkcja
nie jest bezwzględnie całkowalna, choć istnieje
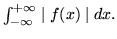
- Wskaż przykłady funkcji spełniających
założenia Twierdzenia Fouriera, oraz takich które
tych założeń nie spełniają.
- Przedstaw funkcję
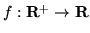 daną
wzorem:
daną
wzorem:
(a)
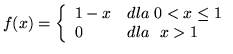
b) 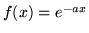 , (
, (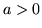 )
)
za pomocą (i) sinusowego (ii) kosinusowego wzoru Fouriera.
- Znajdż widmo, widmo amplitudowe i widmo fazowe funkcji
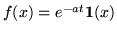 .
.
- Wykaż, że widmo amplitudowe (
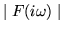 ) jest funkcją
parzystą, zaś widmo fazowe
) jest funkcją
parzystą, zaś widmo fazowe
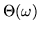 funkcją nieparzystą.
funkcją nieparzystą.
- Podaj transformatę Fouriera funkcji
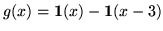 .
Narysuj wykresy części rzeczywistej i urojonej transformaty.
.
Narysuj wykresy części rzeczywistej i urojonej transformaty.
- Znajdż funkcję
 , taką, że
, taką, że
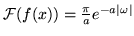 ,
, 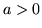 .
.
- Zbadaj które z poniższych funkcji są oryginałami:
(a)
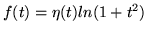
(b)
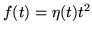
(c)
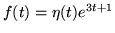
(d)
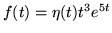
(e)
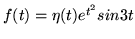
(f)
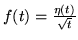
- Wykaż, że jeśli
 jest oryginałem okresowym
o okresie
jest oryginałem okresowym
o okresie 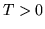 (tzn takim, że dla
(tzn takim, że dla 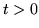
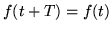 wtedy
wtedy
- Oblicz transformaty oryginałów:
(a) 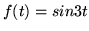
(b)
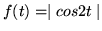
(c)
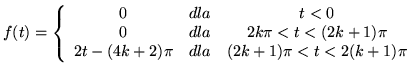
- Dla poniższych równań i układów równań
różniczkowych wskaż całki szczególne przy
pomocy rachunku operatorowego:
(a)
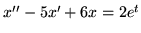
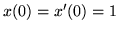
(b)
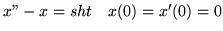
(c)
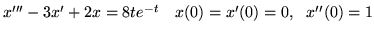
(d)
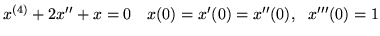
(f)
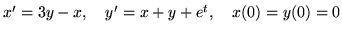
(g)
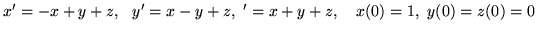
(h)
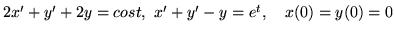
Dystrybucje
- Wykaż, że ciąg
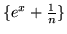 jest podstawowy. Wskaż ciągi
jemu równoważne. Podaj inne przykłady ciągów podstawowych i
takich które podstawowymi nie są.
jest podstawowy. Wskaż ciągi
jemu równoważne. Podaj inne przykłady ciągów podstawowych i
takich które podstawowymi nie są.
- Uzasadnić fakt, że ciąg
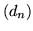
jest podstawowym i definiuje dystrybycję delta Diraca.
- Wykaż, że ciąg
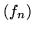 ,
,
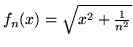 jest podstawowy i definiuje dystrybucję
jest podstawowy i definiuje dystrybucję 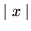 .
.
oblicz pochodną tej dystrybucji. Zauważ, że druga pochodna
dystrybucji 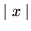 jest równa
jest równa 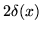
Wskazówka: W tym celu najlepiej wykazać, że ciąg 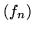 równoważny jest ciągowi
równoważny jest ciągowi 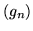




Next: Bibliografia
Up: Zadania z matematyki dla
Previous: Szeregi Fouriera
Contents