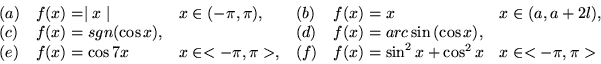Next: Przekształcenia całkowe
Up: Zadania z matematyki dla
Previous: Równania różniczkowe
Contents
- Znajdź iloczyny skalarne funkcji
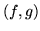 , gdzie
, gdzie
(a)
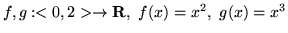
(b)
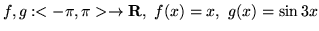 .
.
- Dlaczego odwzorowanie
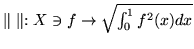 nie jest normą gdy
nie jest normą gdy 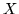 jest zbiorem
funkcji R-całkowalnych w przedziale
jest zbiorem
funkcji R-całkowalnych w przedziale 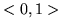 , a jest normą gdy
, a jest normą gdy
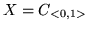 ?
?
- Oblicz normy kwadratowe funkcji
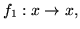
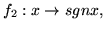
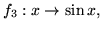
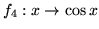 i odległości kwadratowe pomiędzy
i odległości kwadratowe pomiędzy
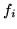 a
a 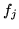 ,
,
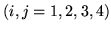 w przedziale
w przedziale 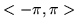 .
.
- Wykaż, że ciąg funkcyjny
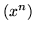 w przedziale
w przedziale 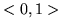 jest
zbieżny przeciętnie z kwadratem do każdej z funkcji:
jest
zbieżny przeciętnie z kwadratem do każdej z funkcji:
Skomentuj!
- Rozwiń w szereg Fouriera funkcje:
- Rozwiń funkcję
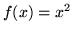
(i) w szereg kosinusów w przedziale 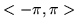
(ii) w szereg sinusów w przedziale 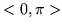
(iii) w szereg Fouriera w przedziale 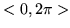
Narysuj wykresy funkcji i wykresy sum ich szeregów Fouriera.
Korzystając z otrzymanych wyników oblicz sumy szeregów:
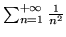 ,
,
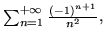
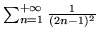 .
.
- Znajdź wielomian
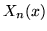 stopnia
stopnia 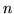 taki, aby
(przy dowolnie ustalonych
taki, aby
(przy dowolnie ustalonych 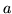 i
i 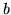 )
dla dowolnego wielomianu
)
dla dowolnego wielomianu 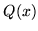 stopnia niższego
niż
stopnia niższego
niż 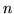 zachodziła równość
zachodziła równość
Wskazówka: Potraktuj wielomian 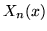 jako pochodną rzędu
jako pochodną rzędu
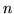 pewnego wielomianu
pewnego wielomianu 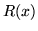 stopnia
stopnia 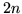 spełniającego warunki:
spełniającego warunki:
- Udowodnij, że ciąg wielomianów Legendre'a
jest układem ortogonalnym funkcji w przedziale 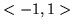 .
.
Wskazówka: Skorzystaj z zadania poprzedniego.




Next: Przekształcenia całkowe
Up: Zadania z matematyki dla
Previous: Równania różniczkowe
Contents