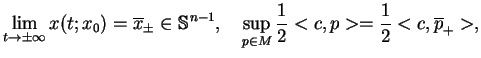Next: Metoda redukcji Hamiltonowskiej dla
Up: Programowanie dynamiczne problemów ekstremalnych.
Previous: Programowanie dynamiczne problemów ekstremalnych.
Spis rzeczy
Metoda redukcji Hamiltonowskej dla problemów PL na
simpleksie.
Rozważmy ideę programowania
dynamicznego na przykładzie rozwiązania problemów PL na
simpleksie. Niech 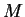 oznacza zwykły simpleks
oznacza zwykły simpleks
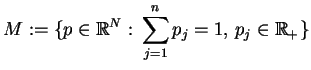 |
(10.1) |
i postawmy taki problem programowanie liniowego na 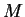 :
:
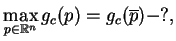 |
(10.2) |
gdzie
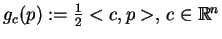 , jest funkcją celu,
, jest funkcją celu,
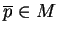 jest punktem osią-gnięcia maksumum w (
jest punktem osią-gnięcia maksumum w (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i
) i
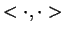 jak zawsze, jest iloczynem skalarnym w
jak zawsze, jest iloczynem skalarnym w
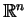 .
.
Jest oczywistym, że problem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma zawsze rozwiązanie
) ma zawsze rozwiązanie
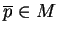 , ponieważ funkcja
, ponieważ funkcja
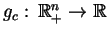 jest ciągła, a
jest ciągła, a 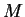 jest
zbiorem zwartym. Żeby podać najprostszą demonstrację metody
redukcji (Hamiltonowskiej), wprowadźmy następne pomocnicze
odwzorowanie sfery
jest
zbiorem zwartym. Żeby podać najprostszą demonstrację metody
redukcji (Hamiltonowskiej), wprowadźmy następne pomocnicze
odwzorowanie sfery
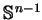 na
na 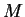 , tj. takie
, tj. takie
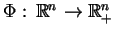 ,
,
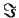
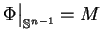 , gdzie
, gdzie
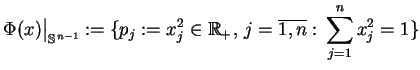 |
(10.3) |
Jest oczywistym z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), że
), że
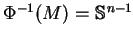 . Niech
. Niech
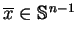 jest punktem ekstremum dla problemu
jest punktem ekstremum dla problemu
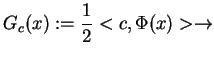 |
(10.4) |
który przez wyrażenie
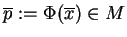 rozwiązuje, oczywiście problem wyjściowy
(
rozwiązuje, oczywiście problem wyjściowy
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Warunek
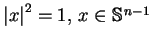 , może być
rozważany jako odwzorowanie
, może być
rozważany jako odwzorowanie
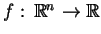 z ograniczeniem
z ograniczeniem
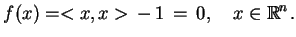 |
(10.5) |
Rozważmy teraz funkcjonał celu
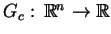 i skonstruujmy dla niego odpowiednie tzw.
gradientowe pole wektorowe
i skonstruujmy dla niego odpowiednie tzw.
gradientowe pole wektorowe
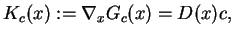 |
(10.6) |
gdzie dla
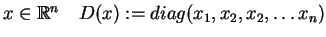 jest macierzą diagonalną.
Pole wektorowe (
jest macierzą diagonalną.
Pole wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) definiuje na
) definiuje na
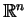 układ dynamiczny
układ dynamiczny
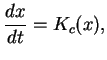 |
(10.7) |
dla którego funkcjonał
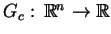 jest, jak to prosto sprawdzić, funkcją Lapunowa,
tj:
jest, jak to prosto sprawdzić, funkcją Lapunowa,
tj:
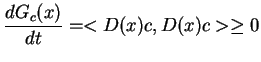 |
(10.8) |
dla wszystkich
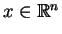 i
i
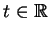 .
Zakładając teraz, że
.
Zakładając teraz, że
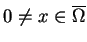 ,
gdzie
,
gdzie
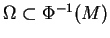 jest pewnym obszarem
w
jest pewnym obszarem
w
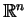 , dość prosto zobaczyć z
(
, dość prosto zobaczyć z
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) że funkcjonał
) że funkcjonał
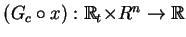 jest
względem parametru
jest
względem parametru
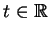 rosnącym wzdłuż
trajektorii pola wektorowego (
rosnącym wzdłuż
trajektorii pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), przyjmując swoje
wartości maksymalne na zwartym zbiorze
), przyjmując swoje
wartości maksymalne na zwartym zbiorze
 . Tę wartość maksymalną dość prosto
obliczyć z takiego warunku:
. Tę wartość maksymalną dość prosto
obliczyć z takiego warunku:
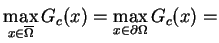 |
(10.9) |
gdzie z definicji, trajektoria
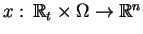 pola wektorowego (
pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) z
warunkiem początkowym w punkcie
) z
warunkiem początkowym w punkcie
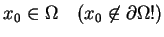 koniecznie przecina brzeg
koniecznie przecina brzeg
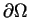 obszaru
obszaru 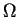 w momencie czasu
w momencie czasu
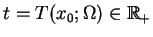 , który prosto znaleźć w sposób analityczny z
warunku
, który prosto znaleźć w sposób analityczny z
warunku
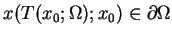 .
Teraz biorąc do uwagi że funkcjonał
.
Teraz biorąc do uwagi że funkcjonał
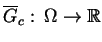 , gdzie
, gdzie
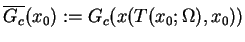 |
(10.10) |
jest zdefiniowany dla wszystkich punktów wewnętrznych
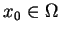 , prosto znajdujemy z (
, prosto znajdujemy z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
dość zręczny algorytm analityczny dla znalezienia ekstremum
(
)
dość zręczny algorytm analityczny dla znalezienia ekstremum
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
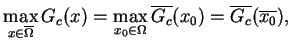 |
(10.11) |
gdzie punkt wewnętrzny
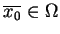 jest
tutaj wyliczany z koniecznego warunku Fermat'a:
jest
tutaj wyliczany z koniecznego warunku Fermat'a:
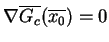 |
(10.12) |
który na mocy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) będzie i wystarczającym.
) będzie i wystarczającym.
Ten algorytm znalezienia ekstremum (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
można także adaptować dla przypadku kiedy zwarty zbiór
)
można także adaptować dla przypadku kiedy zwarty zbiór
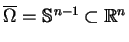 jest mniejszego wymiaru mając miarę Lebesgue'a zero w
jest mniejszego wymiaru mając miarę Lebesgue'a zero w
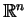 .
.
W tym celu wykorzystamy metodę rzutowania gradientowego
pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na kostyczną przestrzeń
) na kostyczną przestrzeń
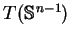 do sfery
do sfery
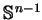 .
Ponieważ przestrzeń styczna
.
Ponieważ przestrzeń styczna
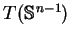 jest
definiowana jako przestrzeń liniowa, prostopadła do wektora
jest
definiowana jako przestrzeń liniowa, prostopadła do wektora
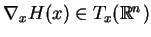 dla każdego
punktu
dla każdego
punktu
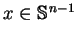 , bo dość prosto
znajdujemy że pole (
, bo dość prosto
znajdujemy że pole (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) zrzutowane na
) zrzutowane na
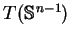 ma postać
ma postać
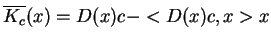 |
(10.13) |
dla każdego
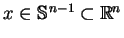 .
.
Teraz znajdujemy się w sytuacji podobnej do opisanej wyżej,
tj. funkcjonał (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) pozostaje funkcją Lapunowa dla
pola wektorowego (
) pozostaje funkcją Lapunowa dla
pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), stycznego do sfery
), stycznego do sfery
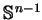 :
:
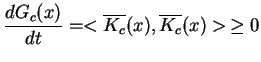 |
(10.14) |
dla wszystkich
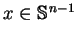 i
i
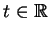 , gdzie
, gdzie
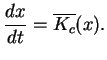 |
(10.15) |
Wyrażenie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma sens dla wszystkich
) ma sens dla wszystkich
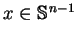 , ponieważ sfera
, ponieważ sfera
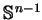 jest
oczywiście niezmienniczym zbiorem dla pola wektorowego
(
jest
oczywiście niezmienniczym zbiorem dla pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w
) w
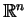 . Biorąc pod uwagę,
że funkcjonał
. Biorąc pod uwagę,
że funkcjonał
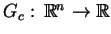 jest w rzeczywistości teraz określony na
jest w rzeczywistości teraz określony na
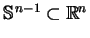 poprzez orbity pola wektorowego
(
poprzez orbity pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na
) na
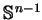 , to można
skonstruować zredukowaną funkcję
, to można
skonstruować zredukowaną funkcję
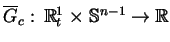 jako
wyrażenie
jako
wyrażenie
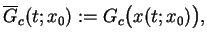 |
(10.16) |
gdzie
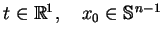 oraz
oraz
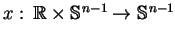 jest odpowiednią orbitą
pola wektorowego (
jest odpowiednią orbitą
pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Ponieważ funkcja
(
). Ponieważ funkcja
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest ograniczona na
) jest ograniczona na
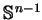 na
mocy jej ciągłości dla wszystkich
na
mocy jej ciągłości dla wszystkich
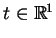 , to istnieją jej ekstremalne wartości przy
, to istnieją jej ekstremalne wartości przy
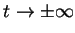 w pewnych punktach
w pewnych punktach
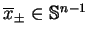 , gdzie względem
(
, gdzie względem
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), pole wektorowe (
), pole wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) zeruje się, tj.
) zeruje się, tj.
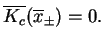 |
(10.17) |
Ostatnie wyrażenie oznacza że punkty osobliwe
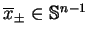 pola wektorowego
(
pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) rozwiązują problem znalezienia ekstermum
(
) rozwiązują problem znalezienia ekstermum
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), a tak więc i problemu programowania liniowego
(
), a tak więc i problemu programowania liniowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na sympleksie
) na sympleksie
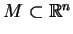 .
Przy tym oczywiście,
.
Przy tym oczywiście,
 , dla dowolnego
, dla dowolnego
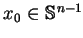 , który oczywiście, nie powinien być punktem
osobliwym. Tak więc wystarczy znaleźć granicę
, który oczywiście, nie powinien być punktem
osobliwym. Tak więc wystarczy znaleźć granicę
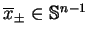 przy pomocy metod
analitycznych lub komputerowo-obliczeniowych, żeby przy pomocy
odwzorowania (
przy pomocy metod
analitycznych lub komputerowo-obliczeniowych, żeby przy pomocy
odwzorowania (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w postaci
) w postaci
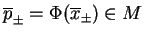 odzyskać rozwiązanie problemu PL (
odzyskać rozwiązanie problemu PL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Przejdziemy teraz do wprowadzenia pojęcia redukcji Hamiltonowskiej
problemów PL. Istota jej polega na znalezieniu pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w postaci równoważnej do odpowiedniej redukcji
Hamiltonowskiej (typu Marsdena - Weinsteina) zastosowanej do
specjalnego Hamiltonowego pola wektorowego na rozszerzonej
przestrzeni fazowej
) w postaci równoważnej do odpowiedniej redukcji
Hamiltonowskiej (typu Marsdena - Weinsteina) zastosowanej do
specjalnego Hamiltonowego pola wektorowego na rozszerzonej
przestrzeni fazowej
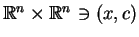 .
.
Jako pierwszy krok tego schematu zadajmy na przestrzeni fazowej
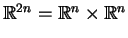 niekanoniczną strukturę
Poissona, tj. ,,nawiasy Poissona''
niekanoniczną strukturę
Poissona, tj. ,,nawiasy Poissona''
w postaci
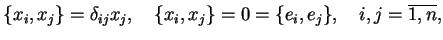 |
(10.18) |
gdzie
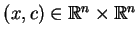 .
Strukturze Poissona (
.
Strukturze Poissona (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) odpowiada tzw. struktura
symlektyczna na
) odpowiada tzw. struktura
symlektyczna na
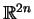 , którą zadaje się
przez 2-formę symplektyczną
, którą zadaje się
przez 2-formę symplektyczną
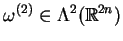 , gdzie
, gdzie
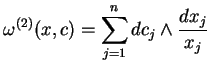 |
(10.19) |
dla wszystkich
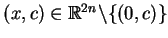 .
.
Struktura symplektyczna (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) (lub struktura (
) (lub struktura (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ))
wybiera się wzglę-dem jednego warunku: gradientowe pole
wektorowe (
))
wybiera się wzglę-dem jednego warunku: gradientowe pole
wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na
) na
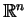 z
dołączonym trywialnym polem wektorowym
z
dołączonym trywialnym polem wektorowym
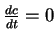 dla
dla
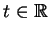 i
i
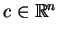 jest równoważne Hamiltonowemu polu wektorowemu
na
jest równoważne Hamiltonowemu polu wektorowemu
na
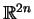 wg. struktury symplektycznej
(
wg. struktury symplektycznej
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i z ustaloną funkcją Hamiltonową
) i z ustaloną funkcją Hamiltonową
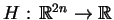 , gdzie w naszym przypadku:
, gdzie w naszym przypadku:
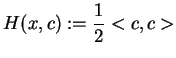 |
(10.20) |
dla wszystkich
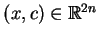 . To znaczy wg.
definicji, że pole wektorowe
. To znaczy wg.
definicji, że pole wektorowe
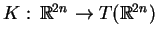 znalezione wg. reguły
znalezione wg. reguły
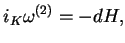 |
(10.21) |
spełnia warunek
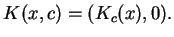 |
(10.22) |
dla wszystkich
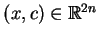 .
.
Formalnie to znaczy wobec struktury symplektycznej (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ),
że jest ona jednym z rozwiązań równania Noether:
),
że jest ona jednym z rozwiązań równania Noether:
 |
(10.23) |
gdzie
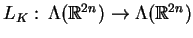 oznacza tzw. pochodną Liego wzdłuż pola
wektorowego
oznacza tzw. pochodną Liego wzdłuż pola
wektorowego
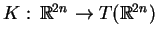 zadanego w postaci (
zadanego w postaci (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Biorąc do uwagi wzór
Cartan'a
). Biorąc do uwagi wzór
Cartan'a
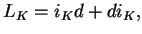 |
(10.24) |
gdzie
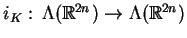 jest odpowiednio różniczkowaniem
wewnętrznym algebry form różniczkowalnych
jest odpowiednio różniczkowaniem
wewnętrznym algebry form różniczkowalnych
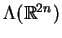 wzdłuż pola wektorowego
wzdłuż pola wektorowego
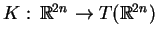 , a
, a
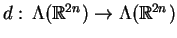 jest
różniczkowaniem zewnętrznym równania (
jest
różniczkowaniem zewnętrznym równania (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) może
być przepisane też w postaci równoważnej jako
) może
być przepisane też w postaci równoważnej jako
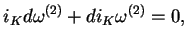 |
(10.25) |
które wg. warunku symplektyczności
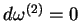 powoduje równość (
powoduje równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Z innej strony, jeśli
wprowadzić skośniesymetrzyczne odwzorowanie
). Z innej strony, jeśli
wprowadzić skośniesymetrzyczne odwzorowanie
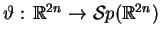 , takie że
, takie że
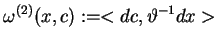 |
(10.26) |
gdzie macierz
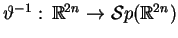 , oczywiście istnieje dla p.w
, oczywiście istnieje dla p.w
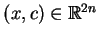 . Wtedy równania
(
. Wtedy równania
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) lub (
) lub (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) będzie liniowym równaniem
na macierz
) będzie liniowym równaniem
na macierz
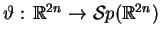 w takiej postaci:
w takiej postaci:
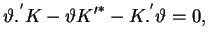 |
(10.27) |
gdzie ,, . '' oznacza zwykłą pochodną Freshet'a odpowiednich
odwzorowań na
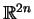 , a ,, * '' oznacza
operację zwykłego sprzężenia wg. iloczynu skalarnego na
, a ,, * '' oznacza
operację zwykłego sprzężenia wg. iloczynu skalarnego na
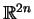 .
.
Po sprawdzenieu bezpośrednio że odwzorowanie
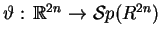 , gdzie
, gdzie
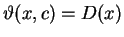 |
(10.28) |
dla wszystkich
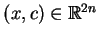 , spełnia
równanie (
, spełnia
równanie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy przy
) otrzymujemy przy 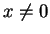 wyrażenie (
wyrażenie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) dla struktury symplektycznej
(
) dla struktury symplektycznej
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na
) na
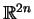 . Wykorzystując dalej
równość (
. Wykorzystując dalej
równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), można znaleźć odpowiednią
funkcję Hamiltonona (
), można znaleźć odpowiednią
funkcję Hamiltonona (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na
) na
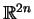 .
.
Teraz jesteśmy w stanie wykonać redukcję Hamiltonowską
dla pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na
) na
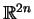 względem komutującego wobec niego pola wektorowego
względem komutującego wobec niego pola wektorowego
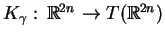 ,
zadanego poprzez funkcję Hamiltona
,
zadanego poprzez funkcję Hamiltona
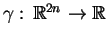 , gdzie
, gdzie
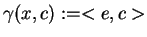 |
(10.29) |
oraz
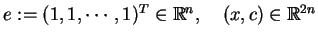 . Jest jasnym że
. Jest jasnym że
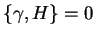 , co
powoduje
, co
powoduje
![$ [K,K_{\gamma}]=0$](img1041.gif) na
na
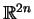 ,
gdzie
,
gdzie
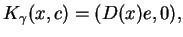 |
(10.30) |
dla wszystkich
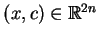 . Redukcja
przestrzeni fazowej
. Redukcja
przestrzeni fazowej
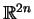 wg. orbit pola
wektorowego (
wg. orbit pola
wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oznacza prosto, że można
skonstruować odwzorowanie równoważności takich punktów
) oznacza prosto, że można
skonstruować odwzorowanie równoważności takich punktów
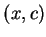 oraz
oraz
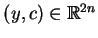 , które
mogą być połączone przez orbitę pola wektorowego
(
, które
mogą być połączone przez orbitę pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Tak więc, opierając się na (
). Tak więc, opierając się na (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ),
to odwzorowanie redukcji
),
to odwzorowanie redukcji
 może być zadane w
postaci dokładnej
może być zadane w
postaci dokładnej
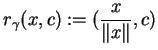 |
(10.31) |
która uwzględnia naszą więź 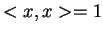 ponieważ
ponieważ
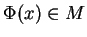 dla wszystkich
dla wszystkich
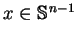 . Rzeczywiście dla wszystkich
. Rzeczywiście dla wszystkich
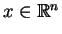 wektor
wektor
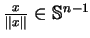 nie zależy od pola wektorowego
(
nie zależy od pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Jest jasnym, że (
). Jest jasnym, że (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) rzutuje
przestrzeń
) rzutuje
przestrzeń
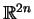 na
na
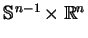 , która jest podstawową dla nas względem
odwzorowanie (
, która jest podstawową dla nas względem
odwzorowanie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i problemu PL (
) i problemu PL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i
(
) i
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Tak więc rzutowanie (
). Tak więc rzutowanie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) rozważemy
jako zadane. Wtedy powstaje problem znalezienia pola wektorowego
(
) rozważemy
jako zadane. Wtedy powstaje problem znalezienia pola wektorowego
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i funkcji Hamiltona (
) i funkcji Hamiltona (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Zróbmy to
w taki sposób: niech punkt
). Zróbmy to
w taki sposób: niech punkt
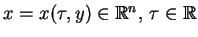 , jest rzutowany poprzez (
, jest rzutowany poprzez (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w
stały punkt
) w
stały punkt
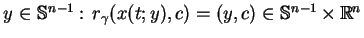 . To znaczy, że pole gradientowe
. To znaczy, że pole gradientowe
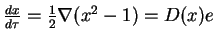 generuje orbitę
generuje orbitę
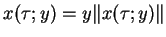 dla każdego
dla każdego
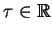 i
i
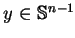 . Stąd znajdujemy wprost
że
. Stąd znajdujemy wprost
że
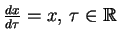 . Wtedy,
oczywi-ście,
. Wtedy,
oczywi-ście,
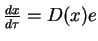 , co daje
dokładnie (
, co daje
dokładnie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Co jeszcze nie sprawdzono, lecz jest
podstawowym, to komutatywność pól wektorowych (
). Co jeszcze nie sprawdzono, lecz jest
podstawowym, to komutatywność pól wektorowych (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
i
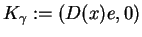 . Ostatnią własność
sprawdzamy wprost. Tak więc, ponieważ jednocześnie zachodzi
równość
. Ostatnią własność
sprawdzamy wprost. Tak więc, ponieważ jednocześnie zachodzi
równość
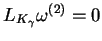 , istnieje
funkcja Hamiltona
, istnieje
funkcja Hamiltona
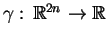 , dokładnie taka jak (
, dokładnie taka jak (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Jako uwagę
przytoczymy tylko wzmiankę o tym że takie pole wektorowe
). Jako uwagę
przytoczymy tylko wzmiankę o tym że takie pole wektorowe
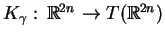 ,
które komutuje z polem (
,
które komutuje z polem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i dokonuje redukcje
) i dokonuje redukcje
 , jest niejedyne i każde może być skonstruowane
w podobny sposób jak wyżej, biorąc gradient funkcji
ograniczenia
, jest niejedyne i każde może być skonstruowane
w podobny sposób jak wyżej, biorąc gradient funkcji
ograniczenia
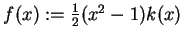 gdzie
gdzie
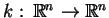 jest a priori p.w.
dodatnia :
jest a priori p.w.
dodatnia :
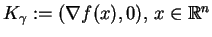 . Na podstawie rzutowania (
. Na podstawie rzutowania (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) można
teraz zrzutować pole wektorowe (
) można
teraz zrzutować pole wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na pole wektorowe
) na pole wektorowe
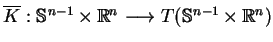 w taki sposób, że zachodzi równość:
w taki sposób, że zachodzi równość:
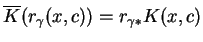 |
(10.32) |
dla wszystkich
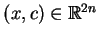 , gdzie
, gdzie
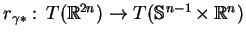 jest odpowiednim do (
jest odpowiednim do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
odwzorowaniem stycznym. Jako wynik tej redukcji na
)
odwzorowaniem stycznym. Jako wynik tej redukcji na
 można
sformułować taki lemat
można
sformułować taki lemat
10.1
Lemat Zredukowane pola wektorowe
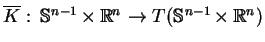
oraz
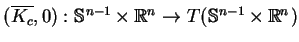
są równe.
 Dowód lematu jest wprost wyliczając wyrażenie
(
Dowód lematu jest wprost wyliczając wyrażenie
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
) 
Ponieważ redukcja (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest
niezmiennicza wg parametru
) jest
niezmiennicza wg parametru
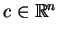 , można
sformułować na podstawie równości
, można
sformułować na podstawie równości
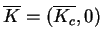 oraz własności
(
oraz własności
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) następu-jące twierdzenie.
) następu-jące twierdzenie.
10.2
Twierdzenie. Punkty krytyczne
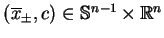
pola wektorowego

spełniają następne
warunki graniczne:
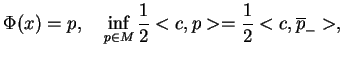 |
(10.33) |
dla każdego nie krytycznego punktu
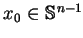
i dowolnego
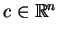
.




Next: Metoda redukcji Hamiltonowskiej dla
Up: Programowanie dynamiczne problemów ekstremalnych.
Previous: Programowanie dynamiczne problemów ekstremalnych.
Spis rzeczy
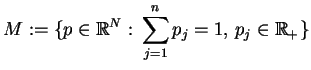
![]() ) ma zawsze rozwiązanie
) ma zawsze rozwiązanie
![]() , ponieważ funkcja
, ponieważ funkcja
![]() jest ciągła, a
jest ciągła, a ![]() jest
zbiorem zwartym. Żeby podać najprostszą demonstrację metody
redukcji (Hamiltonowskiej), wprowadźmy następne pomocnicze
odwzorowanie sfery
jest
zbiorem zwartym. Żeby podać najprostszą demonstrację metody
redukcji (Hamiltonowskiej), wprowadźmy następne pomocnicze
odwzorowanie sfery
![]() na
na ![]() , tj. takie
, tj. takie
![]() ,
,
![]()
![]() , gdzie
, gdzie
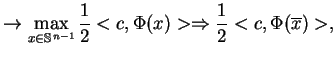
![]() , może być
rozważany jako odwzorowanie
, może być
rozważany jako odwzorowanie
![]() z ograniczeniem
z ograniczeniem
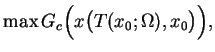
![]() )
można także adaptować dla przypadku kiedy zwarty zbiór
)
można także adaptować dla przypadku kiedy zwarty zbiór
![]() jest mniejszego wymiaru mając miarę Lebesgue'a zero w
jest mniejszego wymiaru mając miarę Lebesgue'a zero w
![]() .
.
![]() ) na kostyczną przestrzeń
) na kostyczną przestrzeń
![]() do sfery
do sfery
![]() .
Ponieważ przestrzeń styczna
.
Ponieważ przestrzeń styczna
![]() jest
definiowana jako przestrzeń liniowa, prostopadła do wektora
jest
definiowana jako przestrzeń liniowa, prostopadła do wektora
![]() dla każdego
punktu
dla każdego
punktu
![]() , bo dość prosto
znajdujemy że pole (
, bo dość prosto
znajdujemy że pole (![]() ) zrzutowane na
) zrzutowane na
![]() ma postać
ma postać
![]() ) pozostaje funkcją Lapunowa dla
pola wektorowego (
) pozostaje funkcją Lapunowa dla
pola wektorowego (![]() ), stycznego do sfery
), stycznego do sfery
![]() :
:
![]() ) w postaci równoważnej do odpowiedniej redukcji
Hamiltonowskiej (typu Marsdena - Weinsteina) zastosowanej do
specjalnego Hamiltonowego pola wektorowego na rozszerzonej
przestrzeni fazowej
) w postaci równoważnej do odpowiedniej redukcji
Hamiltonowskiej (typu Marsdena - Weinsteina) zastosowanej do
specjalnego Hamiltonowego pola wektorowego na rozszerzonej
przestrzeni fazowej
![]() .
.
![]() niekanoniczną strukturę
Poissona, tj. ,,nawiasy Poissona''
niekanoniczną strukturę
Poissona, tj. ,,nawiasy Poissona''
![]() ) (lub struktura (
) (lub struktura (![]() ))
wybiera się wzglę-dem jednego warunku: gradientowe pole
wektorowe (
))
wybiera się wzglę-dem jednego warunku: gradientowe pole
wektorowe (![]() ) na
) na
![]() z
dołączonym trywialnym polem wektorowym
z
dołączonym trywialnym polem wektorowym
![]() dla
dla
![]() i
i
![]() jest równoważne Hamiltonowemu polu wektorowemu
na
jest równoważne Hamiltonowemu polu wektorowemu
na
![]() wg. struktury symplektycznej
(
wg. struktury symplektycznej
(![]() ) i z ustaloną funkcją Hamiltonową
) i z ustaloną funkcją Hamiltonową
![]() , gdzie w naszym przypadku:
, gdzie w naszym przypadku:
![]() ),
że jest ona jednym z rozwiązań równania Noether:
),
że jest ona jednym z rozwiązań równania Noether:
![]() , gdzie
, gdzie
![]() ) na
) na
![]() względem komutującego wobec niego pola wektorowego
względem komutującego wobec niego pola wektorowego
![]() ,
zadanego poprzez funkcję Hamiltona
,
zadanego poprzez funkcję Hamiltona
![]() , gdzie
, gdzie