



Next: Spis rzeczy
Up: Programowanie dynamiczne problemów ekstremalnych.
Previous: Metoda redukcji Hamiltonowskej dla
Spis rzeczy
Rozważmy ogólny problem PL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) na
poliedrze (wielościanie)
) na
poliedrze (wielościanie) 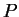 , gdzie
, gdzie
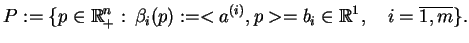 |
(10.34) |
Oczywiście, rozwiązanie problemu PL na poliedrze
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) zawsze istnieje gdy
) zawsze istnieje gdy
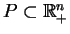 jest zbiorem zwartym.
jest zbiorem zwartym.
W taki sam sposób jak powyżej konstruujemy pole wektorowe
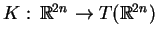 jako pole
gradientowe w postaci
jako pole
gradientowe w postaci
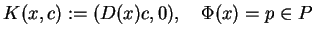 |
(10.35) |
dla wszystkich
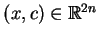 . Rozważmy teraz
ograniczenia
. Rozważmy teraz
ograniczenia
![$\displaystyle f_{j}(x):=\frac{1}{2}[\beta_{j}(\Phi(x))
-b_{j}]=\frac{1}{2}[<a^{(j)}D(x)x> - b_{j}],$](img1077.gif) |
(10.36) |
gdzie
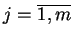 i odpowiednie im pola gradientowe
na
i odpowiednie im pola gradientowe
na
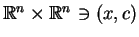 :
:
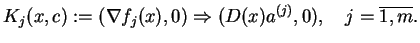 |
(10.37) |
Jest oczywistym sprawdzić, że pola wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
komutują z polem (
)
komutują z polem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), tj.
), tj.
![$\displaystyle [K,K_{j}]=0$](img1079.gif) |
(10.38) |
dla wszystkich
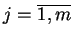 . Oprócz tego, struktura
symplektyczna (
. Oprócz tego, struktura
symplektyczna (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) generowana popzez pole wektorowe
(
) generowana popzez pole wektorowe
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest też niezmiennicza wg pól wektorowych
(
) jest też niezmiennicza wg pól wektorowych
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), tj.
), tj.
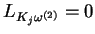 |
(10.39) |
dla każdego
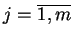 . Stąd wynika, że każde
pole wektorowe (
. Stąd wynika, że każde
pole wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest Hamiltonowskie, tj. istnieją
funkcje
) jest Hamiltonowskie, tj. istnieją
funkcje
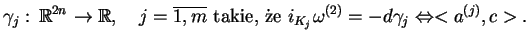 |
(10.40) |
Z drugiej strony pola wektorowe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) komutują też
między sobą, tj.
) komutują też
między sobą, tj.
![$\displaystyle [K_{j},K_{s}]=0$](img1082.gif) |
(10.41) |
dla wszystkich
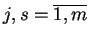 , przy czym przyjmujemy
a priori, że wszystkie pola wektorewe (
, przy czym przyjmujemy
a priori, że wszystkie pola wektorewe (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są
liniowo niezależne.
) są
liniowo niezależne.
Niech teraz moduł liniowy (powłoka)
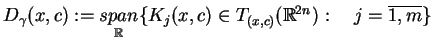 |
(10.42) |
dla wszystkich
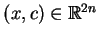 jest
dystrybucją różniczkową
jest
dystrybucją różniczkową
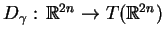 , która generuje rozmaitości całkowe
dla każdego
, która generuje rozmaitości całkowe
dla każdego
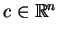 , tworzące
rozwłóknienie
, tworzące
rozwłóknienie
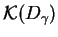 przestrzeni
przestrzeni
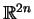 . Ponieważ rozwłóknienie
. Ponieważ rozwłóknienie
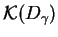 jest niezmiennicze względem pola
wektorowego (
jest niezmiennicze względem pola
wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), można go zredukować na przestrzeń
ilorazową
), można go zredukować na przestrzeń
ilorazową
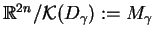 ,
która będzie dyfeomorficzna do rozmaitości
,
która będzie dyfeomorficzna do rozmaitości
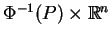 . Niech
. Niech
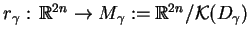 jest
odpowiednim rzutowaniem na
jest
odpowiednim rzutowaniem na
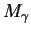 . Wtedy zdefiniowane
pole wektorowe
. Wtedy zdefiniowane
pole wektorowe
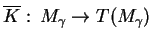 , takie że
, takie że
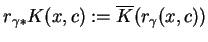 |
(10.43) |
dla wszystkich
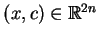 . Pole wektorowe
. Pole wektorowe
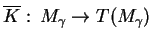 jako
zredukowane gradientowe pole wektorowe spełnia warunek
jako
zredukowane gradientowe pole wektorowe spełnia warunek
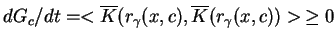 |
(10.44) |
dla wszystkich
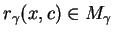 . To
powoduje istnienie granic
. To
powoduje istnienie granic
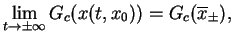 |
(10.45) |
gdzie
 są
punktami krytycznymi pola wektorewego
są
punktami krytycznymi pola wektorewego
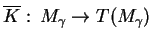 , tj.
, tj.
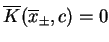 dla wszystkich
zadanych
dla wszystkich
zadanych
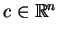 , oraz punkt
, oraz punkt
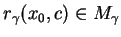 jest dowolny i
niekrytyczny. Pozostaje teraz wypisać w postaci jawnej wyrażenie
dla zredukowanego pola wektorowego
jest dowolny i
niekrytyczny. Pozostaje teraz wypisać w postaci jawnej wyrażenie
dla zredukowanego pola wektorowego
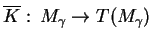 we wspóżzędnych naturalnych na
we wspóżzędnych naturalnych na
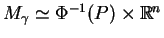 .
Dlatego najpierw skonstruujemy z wektorów
.
Dlatego najpierw skonstruujemy z wektorów
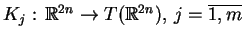 , nowy
zbiór pól wektorowych
, nowy
zbiór pól wektorowych
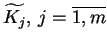 ortogonalnych, tj.
ortogonalnych, tj.
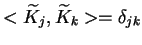 ,
,
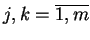 oraz
oraz
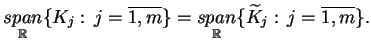 |
(10.46) |
Wtedy, oczywiście, w zmiennych wyjściowych pole wektorowe
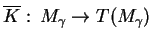 ma taką
postać:
ma taką
postać:
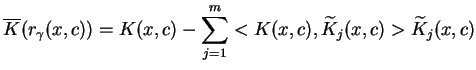 |
(10.47) |
dla wszystkich
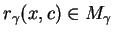 . Wynik
(
. Wynik
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) może być także otrzymany w sposób już
wcześniej zastosowany w rozdziale
) może być także otrzymany w sposób już
wcześniej zastosowany w rozdziale ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , zapisują c
odwzorowanie rzutowania
, zapisują c
odwzorowanie rzutowania
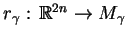 jako złożenie rzutowań
jako złożenie rzutowań
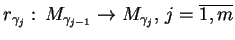 , tj.
, tj.
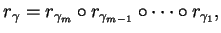 |
(10.48) |
gdzie rzutowania
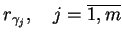 są konstruowane wg defininicji (
są konstruowane wg defininicji (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ):
):
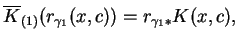 |
(10.49) |
dla wszystkich
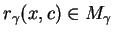 . Tak więc
znajdując granice
. Tak więc
znajdując granice
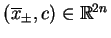 trajektorii pola wektorowego
trajektorii pola wektorowego
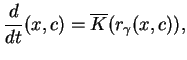 |
(10.50) |
gdzie
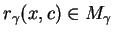 jako
jako
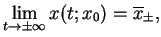 |
(10.51) |
przy warunku, że
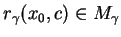 nie
jest punktem krytycznym pola wektorowego (
nie
jest punktem krytycznym pola wektorowego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ),
otrzymujemy rozwiązanie problemu PL (
),
otrzymujemy rozwiązanie problemu PL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i
(
) i
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jako punkty
) jako punkty
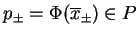 .
LITERATURA.
1. Aubin J.P., L'analyse non linéaire et ses
motivations economiques, Masson, Paris, New York, 1988.
2. Ekeland I., Temam R., Convex analysis and variational
problems, North-Holland Publ. Company, Amsterdam, 1976.
3. Balakrishnan A.V., Applied functional analysis,
Springer Verlag, New York, Barlin, 1976.
4. Alekseev V.M., Tikhomirov V.M., Fomin S.V., Sterowanie
optymalne, Wydawnictwo ''Nauka'', Moskwa, 1979.
5. Rockafellar R.T., Convex analysis, Princeton
University Press, Princeton, 1970.
6. Nirenberg L., Topics in nonlinear functional analysis,
Lecture Notes of NY University, NY, 1974.
7. Faybusovich L., Simplex Method and Groups Generated by
Reflections, Acta Applic. Math, 20, p.231-245, 1990.
8. Megiddo N., Shub M., Boundary behavior of interior
point algorithms in linear programming, Math. of Oper. Res., 14,
N1, p. 97-146, 1989.
9. Bayer D.A., Lagaris J.C., The nonlinear geometry of
linear programming I and II, Trans. AMS, 314, N2, p.499-581, 1989.
10. Faybusovich L., Hamiltonian structure of dynamical
systems which solve linear programming problems, Physica D, 53,
p.217-232, 1991.
11. Prykarpatski A., Mykutyk I., Algebra Integrability of
Nonlinear Dynamical Systems in Manifolds, Kluwer Academic
Publishers, 1998, the Netherlands.
.
LITERATURA.
1. Aubin J.P., L'analyse non linéaire et ses
motivations economiques, Masson, Paris, New York, 1988.
2. Ekeland I., Temam R., Convex analysis and variational
problems, North-Holland Publ. Company, Amsterdam, 1976.
3. Balakrishnan A.V., Applied functional analysis,
Springer Verlag, New York, Barlin, 1976.
4. Alekseev V.M., Tikhomirov V.M., Fomin S.V., Sterowanie
optymalne, Wydawnictwo ''Nauka'', Moskwa, 1979.
5. Rockafellar R.T., Convex analysis, Princeton
University Press, Princeton, 1970.
6. Nirenberg L., Topics in nonlinear functional analysis,
Lecture Notes of NY University, NY, 1974.
7. Faybusovich L., Simplex Method and Groups Generated by
Reflections, Acta Applic. Math, 20, p.231-245, 1990.
8. Megiddo N., Shub M., Boundary behavior of interior
point algorithms in linear programming, Math. of Oper. Res., 14,
N1, p. 97-146, 1989.
9. Bayer D.A., Lagaris J.C., The nonlinear geometry of
linear programming I and II, Trans. AMS, 314, N2, p.499-581, 1989.
10. Faybusovich L., Hamiltonian structure of dynamical
systems which solve linear programming problems, Physica D, 53,
p.217-232, 1991.
11. Prykarpatski A., Mykutyk I., Algebra Integrability of
Nonlinear Dynamical Systems in Manifolds, Kluwer Academic
Publishers, 1998, the Netherlands.




Next: Spis rzeczy
Up: Programowanie dynamiczne problemów ekstremalnych.
Previous: Metoda redukcji Hamiltonowskej dla
Spis rzeczy
![]() jako pole
gradientowe w postaci
jako pole
gradientowe w postaci