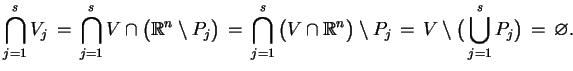Next: Punkty skrajne.
Up: Programowanie matematyczne i układy
Previous: Przestrzenie refleksywne
Spis rzeczy
Rozważmy rodzinę zbiorów wypukłych w
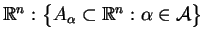 . Wtedy
zachodzi takie twierdzenie
. Wtedy
zachodzi takie twierdzenie
4.1
Twierdzenie Przecięcie dowolnej rodziny zbiorów
wypukłych i domknię-tych jest zbiorem wypukłym.
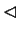 Niech
Niech
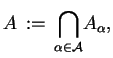 |
(4.1) |
i załóżmy, że punkty 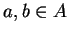 . Wtedy oczywiście dla
. Wtedy oczywiście dla
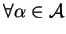 ,
,
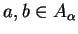 .
Ponieważ zbiory
.
Ponieważ zbiory
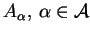 są
wypukłe, mamy dla wszystkich
są
wypukłe, mamy dla wszystkich

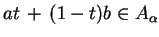 , tj. dla
, tj. dla
![$ t\in [0,1]$](img3.gif)
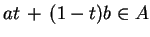 , co dowodzi prawdziwości twierdzenia
, co dowodzi prawdziwości twierdzenia

4.2
Wniosek Niech
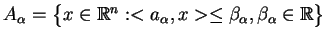
, gdzie

. Wtedy
zbiór
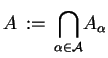 |
(4.2) |
jest wypukły i domknięty, ponieważ każdy zbiór
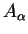
jest też wypukły.
4.3
Definicja Zbiór
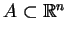
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy poliedrem domkniętym.
W przypadku gdy jądra
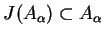 są
niepuste oraz przecięcie
są
niepuste oraz przecięcie
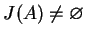 i
i
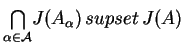 , wtedy jądro
, wtedy jądro 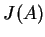 jest otwartym i
wypukłym zbiorem w
jest otwartym i
wypukłym zbiorem w
4.4
Twierdzenie Jeśli
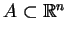
jest
wypukłym zbiorem z niepustym jądrem
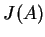
, wtedy
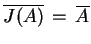
.
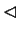 Ponieważ
Ponieważ
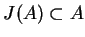 , to
, to
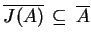 . Niech teraz
. Niech teraz
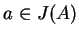 ,
,
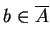 . Ponieważ każdy punkt
odcinka
. Ponieważ każdy punkt
odcinka
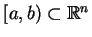 należy do
należy do 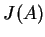 , to
w każdym sąsie-dztwie punktu
, to
w każdym sąsie-dztwie punktu
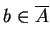 istnieją
punkty z
istnieją
punkty z 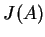 . To znaczy, że
. To znaczy, że
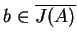 ,
skąd
,
skąd
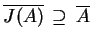 , albo
, albo
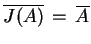

4.5
Twierdzenie Caratheodory'ego Niech
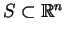
będzie niepustym zbiorem. Wtedy każdy punkt z
powłoki wypukłej
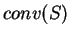
jest wypukłą kombinacją
liniową
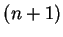
-liczby punktów, lub mniejszej ilości.
4.6
Lemat Radona Każdy zbiór z
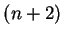
punktów, lub
więcej w
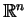
może być rozdzielony na dwa
niepuste podzbiory, wypukłe powłoki które mają wspólny punkt.
 Niech
Niech
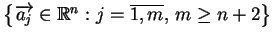 będą wektorami z
będą wektorami z
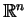 parami różnymi. Rozważmy następujący układ równań
liniowych:
parami różnymi. Rozważmy następujący układ równań
liniowych:
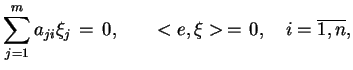 |
(4.3) |
gdzie
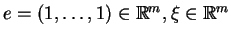 .
.
Liczba równań w (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest mniejsza niż ilość
niewiadomych, tak więc istnieje niezerowy wektor liczb
wśród których są dodatnie, na przykład
) jest mniejsza niż ilość
niewiadomych, tak więc istnieje niezerowy wektor liczb
wśród których są dodatnie, na przykład
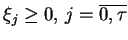 , oraz ujemne
, oraz ujemne
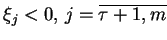 . Wtedy z (
. Wtedy z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
otrzymujemy, że
)
otrzymujemy, że
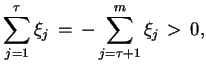 |
(4.4) |
gdzie zachodzi nierówność ostra !
Zapiszmy teraz pierwsze 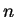 - równań z (
- równań z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w postaci
) w postaci
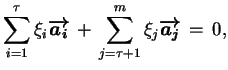 |
(4.5) |
skąd
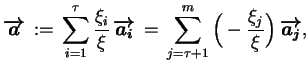 |
(4.6) |
gdzie
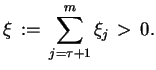 |
(4.7) |
Wykorzystując (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), widzimy z (
), widzimy z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), że
wektor
), że
wektor
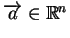 (
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest kombinacją wypukłą punktów
) jest kombinacją wypukłą punktów
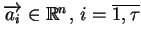 , oraz kombinacją wypukłą
wektorów
, oraz kombinacją wypukłą
wektorów
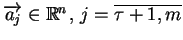 .
.
To znaczy, że
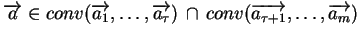 , co dowodzi lemat
, co dowodzi lemat

Dowód twierdzenia Caratheodory'ego:
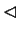 Dla każdego punktu
Dla każdego punktu
 istnieją
wektory
istnieją
wektory
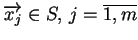 ,
takie, że
,
takie, że
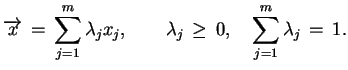 |
(4.8) |
Jeśli 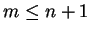 , to twierdzenie jest już udowodnione.
, to twierdzenie jest już udowodnione.
Gdy 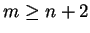 , to dla
, to dla
 spełnione są warunki lematu Radona, tj. istnieje
liczba
spełnione są warunki lematu Radona, tj. istnieje
liczba
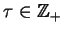 , taka że zbiory
, taka że zbiory
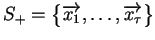 i
i
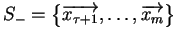 są rozłączne oraz istnieje taki
punkt
są rozłączne oraz istnieje taki
punkt
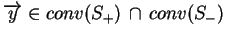 , tj.
, tj.
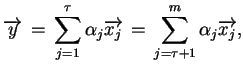 |
(4.9) |
gdzie
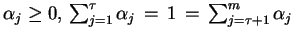 . Niech
. Niech
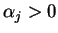 dla
dla
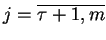 . Wtedy wśród liczb dodatnich
. Wtedy wśród liczb dodatnich
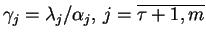 , istnieje najmniejsza, tj. niech
, istnieje najmniejsza, tj. niech
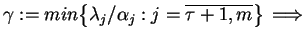 równa na przykład liczbie
równa na przykład liczbie
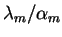
Wówczas mamy:
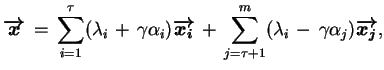 |
(4.10) |
gdzie wszystkie liczby
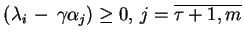 . To znaczy oczywiście, że wektor
. To znaczy oczywiście, że wektor
 jest przedstawiony w
postaci nieujemnej kombinacji liniowej punktów
jest przedstawiony w
postaci nieujemnej kombinacji liniowej punktów
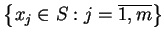 . Ponieważ
liczba
. Ponieważ
liczba
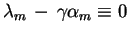 , to z
(
, to z
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) mamy, że
) mamy, że
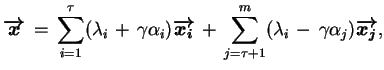 |
(4.11) |
tj.
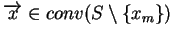 co
przeczy założeniu
co
przeczy założeniu
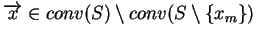 . Tak więc zawsze istnieją punkty
. Tak więc zawsze istnieją punkty
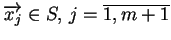 , że
, że
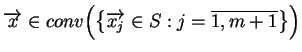 , co dowodzi twierdzenie
, co dowodzi twierdzenie 
Stosownie do zastosowań obrzarów wypukłych, najczęściej cytowanym
jest twierdzenie Helley'a (1913)
4.7
Twierdzenie Helley'a Niech
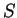
będzie skończoną
rodziną podzbiorów wypukłych w
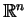
,
złożoną z nie mniej niż
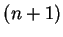
zbiorów. Jeśli każde
z
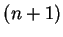
zbiorów z tej rodziny mają punkt wspólny, to
istnieje punkt wspólny dla wszystkich zbiorów z rodziny
Twierdzenie zachodzi też kiedy rodzina
jest nieskończona, a
wszystkie zbiory z
są domknięte i chociaż jeden zbiór jest
zwarty.
 Niech rodzina
Niech rodzina 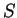 zawiera w sobie
zawiera w sobie 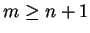 zbiorów
wypukłych
zbiorów
wypukłych
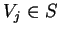 ,
,
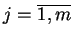 .
Stosujemy metodę indukcji matematycznej:
.
Stosujemy metodę indukcji matematycznej:
Przypuszczamy, że twierdzenie jest prawdziwe dla dowolnej rodziny
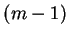 zbiorów,
zbiorów,
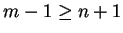 , a nasza rodzina ma
, a nasza rodzina ma
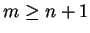 zbiorów. Niech
zbiorów. Niech 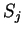 jest rodziną
zbiorów wypukłych, otrzymaną z
jest rodziną
zbiorów wypukłych, otrzymaną z 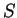 za wyjątkiem zbioru
za wyjątkiem zbioru
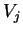 :
Na mocy indukcji rodzina
:
Na mocy indukcji rodzina 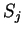 ma dokładnie
ma dokładnie
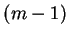 zbiorów, tj. dla każdego
zbiorów, tj. dla każdego
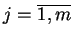 istnieje punkt
istnieje punkt
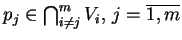 . Do zbioru
wektorów
. Do zbioru
wektorów
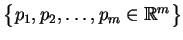 można zastosować twierdzenie Radona,
ponieważ
można zastosować twierdzenie Radona,
ponieważ
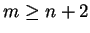 . Wtedy istnieją dwa niepuste
podzbiory
. Wtedy istnieją dwa niepuste
podzbiory
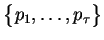 oraz
oraz
 , takie że
przecięcie
, takie że
przecięcie
 jest niepuste! Niech wówczas
jest niepuste! Niech wówczas
 . Ponieważ
. Ponieważ
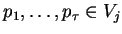 , gdzie
, gdzie
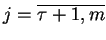 ,
,
to
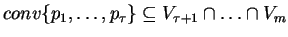 .
.
Podobnie
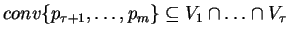 .
.
Tak więc
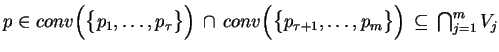 ,
,
co należało dowieść 
 W przypadku gdy rodzina
W przypadku gdy rodzina 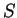 jest nieskończona,
jest nieskończona,
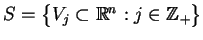 ,
,
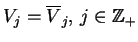 ,
przypuśćmy, że
,
przypuśćmy, że
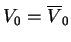 jest zbiorem
zwartym. Wtedy jeżeli z
jest zbiorem
zwartym. Wtedy jeżeli z 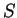 wybierzemy dowolną skończoną
podrodzinę
wybierzemy dowolną skończoną
podrodzinę
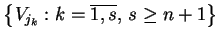 , to na mocy Tw. Helley'a dla skończonej rodziny zbiorów
wypukłych przecięcie
, to na mocy Tw. Helley'a dla skończonej rodziny zbiorów
wypukłych przecięcie
jest niepuste! Tak więc rodzina wszystkich zbiorów
stanowi rodzinę centrowaną podzbiorów domkniętych i
wypukłych w zbiorze 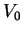 ! Ponieważ zbiór
! Ponieważ zbiór
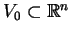 jest zwarty, otrzymujemy
natychmiast, że
jest zwarty, otrzymujemy
natychmiast, że
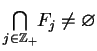 . Ale wówczas też
. Ale wówczas też
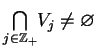

Jako ciekawy dla zastosowań wniosek sformułujemy
następujące twierdzenie.
4.8
Twierdzenie Jeżeli zbiór wypukły jest pokryty przy
pomocy otwartych lub domkniętych półprzestrzeni
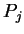
,
gdzie
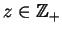
jest skończone! Wtedy ten
zbiór jest pokryty przy pomocy jakichkolwiek
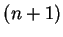
lub
mniej z tych półprzestrzeni.
 Niech teraz zbiór
Niech teraz zbiór
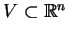 jest taki, że
jest taki, że
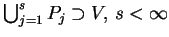 . Odpowiednie
dopełnienia
. Odpowiednie
dopełnienia
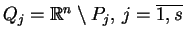 , są też półprzestrzeniami w
, są też półprzestrzeniami w
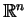 , i przecięcia
, i przecięcia
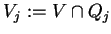 są wypukłymi zbiorami. Odpowiednie przecięcie
są wypukłymi zbiorami. Odpowiednie przecięcie
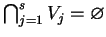 , ponieważ
, ponieważ
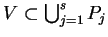 :
:
Stąd na mocy Tw. Helley'a koniecznie istnieje nie mniej niż
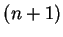 zbiorów
zbiorów
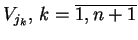 ,
takich których przecięcie jest również puste.
,
takich których przecięcie jest również puste.
Wtedy oczywiście półprzestrzenie
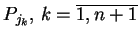 , pokrywają zbiór
, pokrywają zbiór 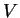 , tj.
, tj.
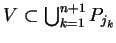 , ponieważ
, ponieważ
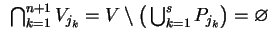





Next: Punkty skrajne.
Up: Programowanie matematyczne i układy
Previous: Przestrzenie refleksywne
Spis rzeczy
![]() . Wtedy
zachodzi takie twierdzenie
. Wtedy
zachodzi takie twierdzenie
![]() są
niepuste oraz przecięcie
są
niepuste oraz przecięcie
![]() i
i
![]() , wtedy jądro
, wtedy jądro ![]() jest otwartym i
wypukłym zbiorem w
jest otwartym i
wypukłym zbiorem w
![]()
![]() Niech
Niech
![]() będą wektorami z
będą wektorami z
![]() parami różnymi. Rozważmy następujący układ równań
liniowych:
parami różnymi. Rozważmy następujący układ równań
liniowych:
![]() Dla każdego punktu
Dla każdego punktu
![]() istnieją
wektory
istnieją
wektory
![]() ,
takie, że
,
takie, że
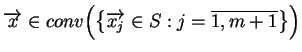 , co dowodzi twierdzenie
, co dowodzi twierdzenie ![]() Niech rodzina
Niech rodzina ![]() zawiera w sobie
zawiera w sobie ![]() zbiorów
wypukłych
zbiorów
wypukłych
![]() ,
,
![]() .
Stosujemy metodę indukcji matematycznej:
.
Stosujemy metodę indukcji matematycznej:
 jest niepuste! Niech wówczas
jest niepuste! Niech wówczas
 . Ponieważ
. Ponieważ
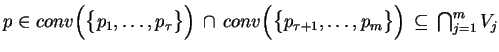 ,
,
![]() W przypadku gdy rodzina
W przypadku gdy rodzina ![]() jest nieskończona,
jest nieskończona,
![]() ,
,
![]() ,
przypuśćmy, że
,
przypuśćmy, że
![]() jest zbiorem
zwartym. Wtedy jeżeli z
jest zbiorem
zwartym. Wtedy jeżeli z ![]() wybierzemy dowolną skończoną
podrodzinę
wybierzemy dowolną skończoną
podrodzinę
![]() , to na mocy Tw. Helley'a dla skończonej rodziny zbiorów
wypukłych przecięcie
, to na mocy Tw. Helley'a dla skończonej rodziny zbiorów
wypukłych przecięcie
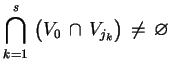
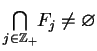 . Ale wówczas też
. Ale wówczas też
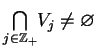
![]() Niech teraz zbiór
Niech teraz zbiór
![]() jest taki, że
jest taki, że
![]() . Odpowiednie
dopełnienia
. Odpowiednie
dopełnienia
![]() , są też półprzestrzeniami w
, są też półprzestrzeniami w
![]() , i przecięcia
, i przecięcia
![]() są wypukłymi zbiorami. Odpowiednie przecięcie
są wypukłymi zbiorami. Odpowiednie przecięcie
![]() , ponieważ
, ponieważ
![]() :
: