



Next: Zbiory wypukłe w
Up: Programowanie matematyczne i układy
Previous: Słaba zbieżność i słaba
Spis rzeczy
Jest oczywiste, że każdy zbiór zwarty w
przestrzeni Banacha
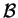 jest także słabo
zwarty. Odwrotnie nie jest poprawnie.
jest także słabo
zwarty. Odwrotnie nie jest poprawnie.
Na przykład zbiór
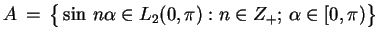 jest słabo zwartym w
jest słabo zwartym w
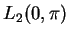 , lecz
nie jest zwartym. (W przypadku gdy
, lecz
nie jest zwartym. (W przypadku gdy
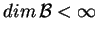 twierdzenie odwrotne też jest
prawdziwe).
twierdzenie odwrotne też jest
prawdziwe).
Ponieważ każdy słabo zwarty zbiór jest słabo
domkniętym, to jest sens rozpatrywać związek pomiędzy
domkniętymi i słabo domkniętymi zbiorami.
3.1
Lemat Każdy słabo domknięty zbiór jest domknięty w
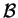
.
Niech
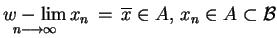 dla
dla
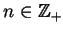 . To znaczy, że dla
. To znaczy, że dla
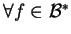
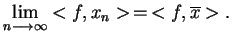 |
(3.1) |
Weźmy teraz ciąg
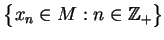 taki, że
taki, że
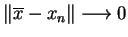 gdy
gdy
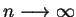 , tj.
, tj.
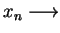 silnie, i taki ciąg oczywiście istnieje. Rozpatrzmy teraz
słabą granicę
silnie, i taki ciąg oczywiście istnieje. Rozpatrzmy teraz
słabą granicę
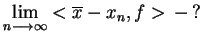 .
Ponieważ z (
.
Ponieważ z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
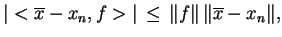 |
(3.2) |
dla wszystkich
 , to z (
, to z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
otrzymujemy, że
tj.
)
otrzymujemy, że
tj.
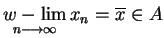 , co znaczy że zbiór
, co znaczy że zbiór
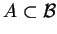 jest
domknięty.
jest
domknięty.
Domknięty zbiór na ogół nie powinien być słabo
domkniętym. Jak powyżej
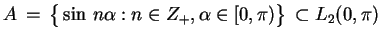 jest
domkniętym lecz nie słabo domkniętym zbiorem.
jest
domkniętym lecz nie słabo domkniętym zbiorem.
Następne twierdzenie jest charakterystyczne dla zbiorów
słabo domkniętych.
3.2
Twierdzenie Każdy wypukły domknięty zbiór jest słabo
domkniętym.
Dla dowodu tego twierdzenia potrzebny jest następujący
lemat Mazura.
3.3
Lemat Mazura Niech
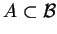
będzie
domkniętym zbiorem oraz
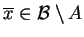
. Wtedy istnieje ciągły liniowy
funkcjonał oddzielający ostro
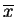
oraz

.
Dla jego dowodu potrzebujemy niektóre własności zbiorów
wypukłych w
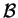 . Niech
. Niech
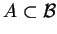 będzie ciałem wypukłym jądra
będzie ciałem wypukłym jądra 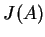 , które zawiera w
sobie
, które zawiera w
sobie
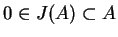 .
.
3.4
Definicja Jądro
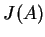
zbioru wypukłego
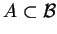
jest to zbiór wszystkich

, takich
że
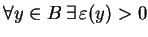
, że
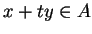
jeśli
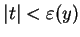
3.5
Definicja Wypukły zbiór,którego jądro
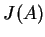
jest
niepuste nazywamy
wypukłym ciałem
3.6
Definicja Funkcjonał
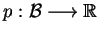
nazywany jest
jednorodnie wypukłym gdy
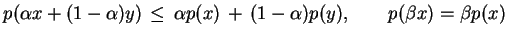 |
(3.3) |
dla
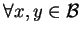
i
![$ \alpha\in [0,1],\,\beta\in
R^{1}_{+}$](img79.gif)
.
3.7
Definicja (
Funkcjonał Minkowskiego)
Niech
będzie wypukłym ciałem w
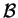
i
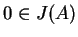
. Wtedy funkcjonał
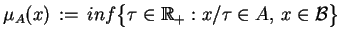 |
(3.4) |
jest
jednorodnie wypukły. Na odwrót, gdy
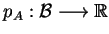
jest
jednolicie wypukłym na
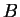
funkcjonałem, to zbiór
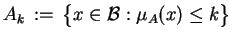 |
(3.5) |
jest ciałem wypukłym, zawierającym punkt
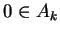
.
Gdy
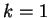
, wtedy
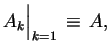 |
(3.6) |
to jest
jądro
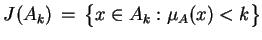
Teraz sformułujemy następnny lemat o oddzielaniu
zbiorów wypukłych. (BARDZO WAŻNY!)
3.8
Lemat Niech
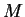
i
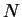
będą zbiorami wypukłymi w
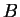
, i
jądro
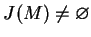
(na przykład), oraz
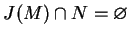
. Wtedy istnieje nietrywialny
liniowy funkcjonał na
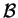
, który oddziela te zbiory
Mówimy, że dwa zbiory 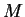 i
i 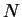 są oddzielone przy
pomocy funkcjonału liniowego
są oddzielone przy
pomocy funkcjonału liniowego
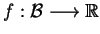 , gdy
, gdy
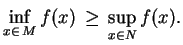 |
(3.7) |
Metodą przesunięcia zbiorów 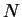 i
i 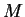 można spełnić
następny warunek: punkt
można spełnić
następny warunek: punkt
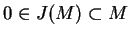 . Niech teraz
. Niech teraz
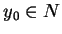 , wtedy punkt
, wtedy punkt
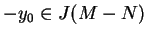 , a
punkt
, a
punkt
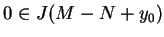 . Ponieważ
. Ponieważ
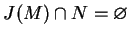 , to
, to
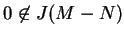 i
i
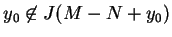 .
.
Niech teraz
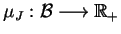 jest funkcjonałem Minkowskiego dla zbioru
jest funkcjonałem Minkowskiego dla zbioru
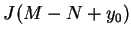 . Wtedy
. Wtedy
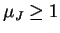 bowiem
bowiem
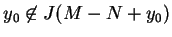 (!).
(!).
Zdefiniujmy teraz liniowy funkcjonał
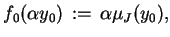 |
(3.8) |
który jest określony na jednowymiarowej
przestrzeni
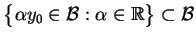 , i spełnia warunek
, i spełnia warunek
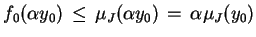 |
(3.9) |
dla wszystkich
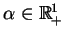 , oraz
, oraz
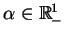
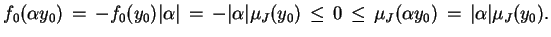 |
(3.10) |
Teraz na mocy Twierdzenia Hana-Banacha funkcjonał
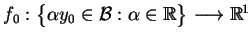 może być
przedłużony do funkcjonału liniowego
może być
przedłużony do funkcjonału liniowego
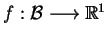 spełniającego następującą nierówność na
spełniającego następującą nierówność na
 :
:
 |
(3.11) |
Stąd wynika, że 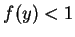 dla
dla
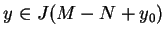 i jednocześnie
i jednocześnie
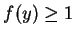 . Tym samym funkcjonał
. Tym samym funkcjonał
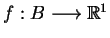 oddziela
zbiory
oddziela
zbiory
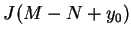 i
i 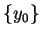 , co znaczy, że
, co znaczy, że 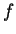 oddziela zbiory
oddziela zbiory 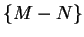 i
i
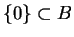 . A
wtedy
. A
wtedy 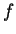 oddziela zbiory
oddziela zbiory 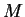 i
i 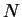

3.9
Wniosek (o oddzielaniu zbiorów wypukłych).
Niech

,
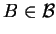
są zbiorami wypukłymi w
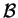
, oraz
na przykład

jest ciałem wypukłym i jego jądro
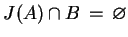
. Wtedy istnieje
niezerowy funkcjonał liniowy i ciągły oddzielający
zbiory

i
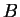
.
Istnienie funkcjonału
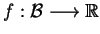 , który oddziela
zbiory
, który oddziela
zbiory  i
i 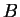 wynika z lematu (
wynika z lematu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Wystarczy teraz
udowodnić tylko, że jest on ciągły. Rzeczywiście, ponieważ
). Wystarczy teraz
udowodnić tylko, że jest on ciągły. Rzeczywiście, ponieważ
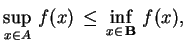 |
(3.12) |
to funkcjonał
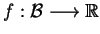 jest ograniczony na
jest ograniczony na  z góry (!). Niech
z góry (!). Niech
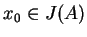 będzie punktem wewnętrznym zbioru
będzie punktem wewnętrznym zbioru  i
i
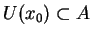 będzie jego otoczeniem
kulistym. Na podstawie (
będzie jego otoczeniem
kulistym. Na podstawie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) funkcjonał
) funkcjonał
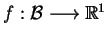 jest
ograniczony na
jest
ograniczony na 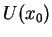 z góry. Ale wtedy jest on
na
z góry. Ale wtedy jest on
na 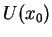 ograniczony też z dołu !.
Ponieważ funkcjonał
ograniczony też z dołu !.
Ponieważ funkcjonał
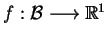 jest ograniczony (!) na
jest ograniczony (!) na 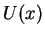 , jest on
ciągły na
, jest on
ciągły na 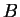 .
.
3.10
Wniosek Niech
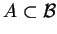
jest
wypukłym, domkniętym zbiorem w przestrzeni unormowanej
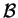
i
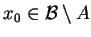
. Wtedy
istnieje ciągły funkcjonał liniowy oddzielający ostro zbiór

i punkt
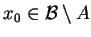
.
Rzeczywiście, niech kula
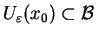 będzie wypukłym otoczeniem punktu
będzie wypukłym otoczeniem punktu
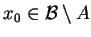 , takie że (o promieniu
, takie że (o promieniu
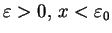 )
)
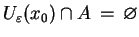 |
(3.13) |
i rozważmy funkcjonał
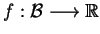 ciągły, liniowy, który oddziela zbiory
ciągły, liniowy, który oddziela zbiory  oraz
oraz
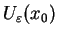 . Wtedy oczywiście
. Wtedy oczywiście
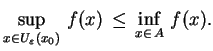 |
(3.14) |
Przypomnijmy teraz sobie, że funkcjonał
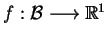 jest
zdefiniowany jako funkcjonał Minkowskiego, tj.
jest
zdefiniowany jako funkcjonał Minkowskiego, tj.
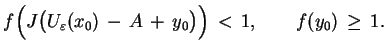 |
(3.15) |
dla każdego
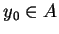 . Z (
. Z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy
) otrzymujemy
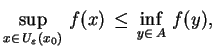 |
(3.16) |
dla
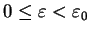 .
.
Zauważmy teraz, że
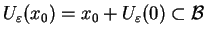 , gdzie
, gdzie
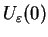 jest otwartym
otoczeniem zera
jest otwartym
otoczeniem zera
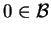 . Ponieważ funkcjonał
. Ponieważ funkcjonał
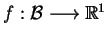 jest liniowy
i ograniczony na
jest liniowy
i ograniczony na 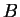 , to z (
, to z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) znajdujemy:
) znajdujemy:
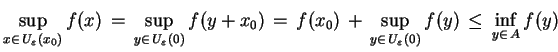 |
(3.17) |
Korzystając z tego, że
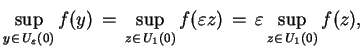 |
(3.18) |
z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) znajdujemy, że dla
) znajdujemy, że dla
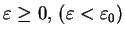
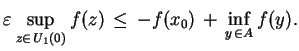 |
(3.19) |
Ponieważ zbiór
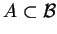 jest domknięty to
istnieje punkt
jest domknięty to
istnieje punkt
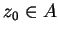 taki, że
taki, że
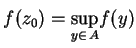 . Wtedy z
(
. Wtedy z
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy:
) otrzymujemy:
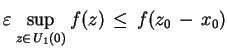 |
(3.20) |
dla każdego
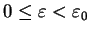 . Przy
. Przy
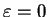 z (
z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy, że
) otrzymujemy, że
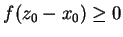 . Dalej mamy dwa przypadki:
. Dalej mamy dwa przypadki:
i)
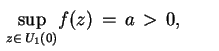 ii)
ii)
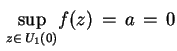
Dla i) mamy:
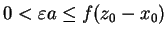 , tj.
oddzielenie
, tj.
oddzielenie  i
i 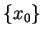 jest ostre. Z ii) mamy, że
jest ostre. Z ii) mamy, że
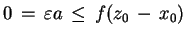 |
(3.21) |
dla
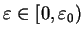 . Ponieważ
(
. Ponieważ
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oznacza, że
otrzymujemy ostre oddzielenie zbiorów
) oznacza, że
otrzymujemy ostre oddzielenie zbiorów  i
i 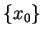 . Teraz
mamy tylko udowodnić, że nigdy
. Teraz
mamy tylko udowodnić, że nigdy
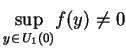 , gdzie
, gdzie
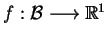 jest
liniowym, ograniczonym (ciągłym) funkcjonałem, nietrywialnym na
jest
liniowym, ograniczonym (ciągłym) funkcjonałem, nietrywialnym na
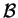 . Ponieważ z (
. Ponieważ z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
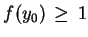 , wnioskujemy że
, wnioskujemy że
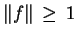 .
.
Z drugiej strony mamy z warunku
że
tj.
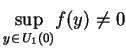 , co dowodzi
nasz wniosek
, co dowodzi
nasz wniosek 
3.11
Wniosek(
lemat o anulatorze) Dla każdej
domkniętej podprzestrzeni
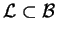
, przestrzeni Banacha
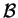
istnieje
niezerowy ciągły, liniowy funkcjonał
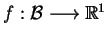
, równy zeru na
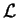
.
Rzeczywiście niech
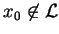 oraz
oraz
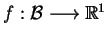 jest
ciągłym funkcjonałem, ostro oddzielającym punkt
jest
ciągłym funkcjonałem, ostro oddzielającym punkt
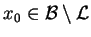 oraz
oraz
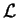 :
:
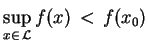 |
(3.22) |
Wtedy
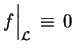 ponieważ górna
granica w (
ponieważ górna
granica w (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) byłaby
) byłaby 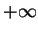 , co jest niemożliwe.
Taki funkcjonał nazywany jest anulatorem podprzestrzeni
, co jest niemożliwe.
Taki funkcjonał nazywany jest anulatorem podprzestrzeni
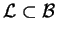 .
.
3.12
Wniosek Jeśli
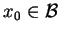
jest
niezerowym elementem przestrzeni unormowanej
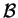
, to
istnieje ciągły, liniowy funkcjonał
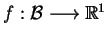
taki, że
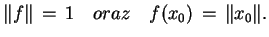 |
(3.23) |
Zdefiniujmy funkcjonał
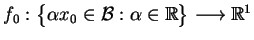 jako
jako
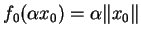 , a dalej przedłużmy
go , nie zmieniając normy, na całą przestrzeń
, a dalej przedłużmy
go , nie zmieniając normy, na całą przestrzeń
 .
Wtedy będą spełnione warunki (
.
Wtedy będą spełnione warunki (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Teraz możemy podać dowód Twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , biorąc
pod uwagę, że wniosek (
, biorąc
pod uwagę, że wniosek (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest dokładnie lematem
Mazura (
) jest dokładnie lematem
Mazura (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Dowód Twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) Zbudujemy sprzeczność. To
znaczy, że istnieje wypukły domknięty i niepusty zbiór
Zbudujemy sprzeczność. To
znaczy, że istnieje wypukły domknięty i niepusty zbiór
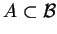 , który NIE jest słabo
domknięty. Wtedy można znaleźć ciąg
, który NIE jest słabo
domknięty. Wtedy można znaleźć ciąg
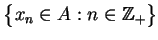 taki, że
taki, że
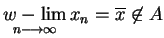 .
.
Niech teraz
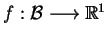 jest
liniowym, ciągłym funkcjonałem istniejącym na mocy
lematu Mazura 3.3, takim że zachodzi ostra
nierówność:
jest
liniowym, ciągłym funkcjonałem istniejącym na mocy
lematu Mazura 3.3, takim że zachodzi ostra
nierówność:
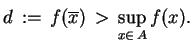 |
(3.24) |
Ponieważ
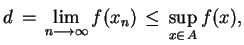 |
(3.25) |
z nierówności (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy,
że
) otrzymujemy,
że
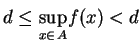 , co jest
niemożli-we. To znaczy, że
, co jest
niemożli-we. To znaczy, że
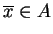 , tj.
zbiór
, tj.
zbiór  jest słabo domknięty
jest słabo domknięty 
3.13
Definicja Przestrzeń Banacha
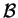
jest nazywana
refleksywną, jeżeli każdy
ograniczony i
domknięty zbiór
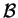
jest
słabo zwarty.
Kilka własności przestrzeni zwartych:
- i)
- Domknięta podprzestrzeń dowolnej przestrzeni
refleksywnej jest sama przestrzenią refleksywną
- ii)
- Produkt
prosty przestrzeni refleksywnych jest przestrzenią refleksywną
- iii)
- Każda przestrzeń Hilberta jest refleksywną
- iv)
- Przestrzenie
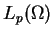 są refleksywne tylko dla
wszystkich
są refleksywne tylko dla
wszystkich 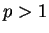
- v)
- Przestrzenie
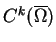 nie są
refleksywne
nie są
refleksywne
- vi)
- Przestrzenie
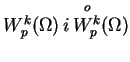 są refleksywne, a
są refleksywne, a
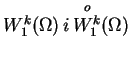 nie.
nie.
3.14
Lemat Funkcjonał
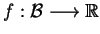
w przestrzeni Banacha
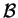
jest
słabo semi-ciągłym z dołu na zbiorze
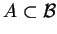
gdy dla każdego

zbiór
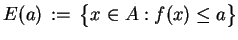 |
(3.26) |
jest słabo domknięty w
 Niech
Niech
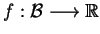 jest słabo
semi-ciągłym fynkcjonałem. Niech
jest słabo
semi-ciągłym fynkcjonałem. Niech
 oraz
oraz
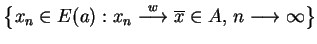 . Wtedy
oczywiście, na mocy definicji
. Wtedy
oczywiście, na mocy definicji
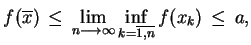 |
(3.27) |
i tym samym
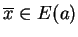 , tj. zbiór
, tj. zbiór 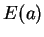 jest
słabo domknięty. Z drugiej strony, niech zbiór
jest
słabo domknięty. Z drugiej strony, niech zbiór 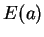 jest
słabo domkniętym dla każdego
jest
słabo domkniętym dla każdego
 i
załóżmy, że funkcjonał
i
załóżmy, że funkcjonał
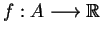 nie jest słabo ciągły z dołu na
nie jest słabo ciągły z dołu na  . Wtedy istnieje element
. Wtedy istnieje element
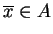 oraz ciąg
oraz ciąg
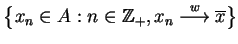 takie, że
takie, że
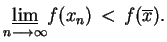 |
(3.28) |
Niech teraz
 jest taki, że spełnione są
nierówności:
jest taki, że spełnione są
nierówności:
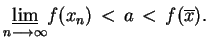 |
(3.29) |
Wtedy istnieje podciąg
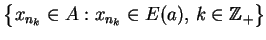 , że
, że
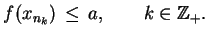 |
(3.30) |
Ponieważ 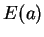 jest słabo domkniętym zbiorem, to
jest słabo domkniętym zbiorem, to
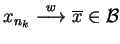 , to
, to
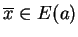 . To znaczy
wówczas, że z (
. To znaczy
wówczas, że z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) zachodzi
) zachodzi
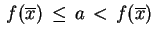 , co jest
sprzeczne. To znaczy, że
, co jest
sprzeczne. To znaczy, że
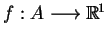 jest semi-ciągłym z dołu
jest semi-ciągłym z dołu 
Zbiór
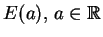 jest słabo domknięty,
jeśli jest domknięty i wypukły, co mamy na mocy Twierdzenia
jest słabo domknięty,
jeśli jest domknięty i wypukły, co mamy na mocy Twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
Prawdziwe jest takie twierdzenie
3.15
Twierdzenie Ciągły, wypukły na domkniętym zbiorze

funkcjonał
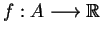
jest słabo
semi-ciągłym na

z dołu.
3.16
Uwaga Nie każdy ciągły funkcjonał jest słabo
semi-ciągły z dołu. Jako przykład można rozważyć
funkcjonał
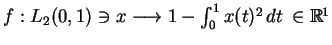
.
Łącząc poprzednie twierdzenia otrzymujemy takie twierdzenie.




Next: Zbiory wypukłe w
Up: Programowanie matematyczne i układy
Previous: Słaba zbieżność i słaba
Spis rzeczy
![]() jest także słabo
zwarty. Odwrotnie nie jest poprawnie.
jest także słabo
zwarty. Odwrotnie nie jest poprawnie.
![]() jest słabo zwartym w
jest słabo zwartym w
![]() , lecz
nie jest zwartym. (W przypadku gdy
, lecz
nie jest zwartym. (W przypadku gdy
![]() twierdzenie odwrotne też jest
prawdziwe).
twierdzenie odwrotne też jest
prawdziwe).
![]() jest
domkniętym lecz nie słabo domkniętym zbiorem.
jest
domkniętym lecz nie słabo domkniętym zbiorem.
![]() . Niech
. Niech
![]() będzie ciałem wypukłym jądra
będzie ciałem wypukłym jądra ![]() , które zawiera w
sobie
, które zawiera w
sobie
![]() .
.
![]() jest funkcjonałem Minkowskiego dla zbioru
jest funkcjonałem Minkowskiego dla zbioru
![]() . Wtedy
. Wtedy
![]() bowiem
bowiem
![]() (!).
(!).
![]() , który oddziela
zbiory
, który oddziela
zbiory ![]() i
i ![]() wynika z lematu (
wynika z lematu (![]() ). Wystarczy teraz
udowodnić tylko, że jest on ciągły. Rzeczywiście, ponieważ
). Wystarczy teraz
udowodnić tylko, że jest on ciągły. Rzeczywiście, ponieważ
![]() będzie wypukłym otoczeniem punktu
będzie wypukłym otoczeniem punktu
![]() , takie że (o promieniu
, takie że (o promieniu
![]() )
)
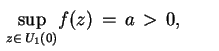 ii)
ii)
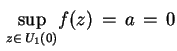
![]() , tj.
oddzielenie
, tj.
oddzielenie ![]() i
i ![]() jest ostre. Z ii) mamy, że
jest ostre. Z ii) mamy, że
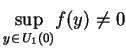 , gdzie
, gdzie
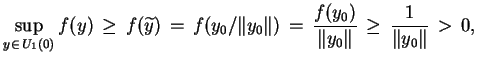
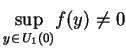 , co dowodzi
nasz wniosek
, co dowodzi
nasz wniosek 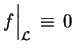 ponieważ górna
granica w (
ponieważ górna
granica w (![]() jako
jako
![]() , a dalej przedłużmy
go , nie zmieniając normy, na całą przestrzeń
, a dalej przedłużmy
go , nie zmieniając normy, na całą przestrzeń
![]() .
Wtedy będą spełnione warunki (
.
Wtedy będą spełnione warunki (![]() ).
).
![]() , biorąc
pod uwagę, że wniosek (
, biorąc
pod uwagę, że wniosek (![]() ) jest dokładnie lematem
Mazura (
) jest dokładnie lematem
Mazura (![]() ).
).
![]() Zbudujemy sprzeczność. To
znaczy, że istnieje wypukły domknięty i niepusty zbiór
Zbudujemy sprzeczność. To
znaczy, że istnieje wypukły domknięty i niepusty zbiór
![]() , który NIE jest słabo
domknięty. Wtedy można znaleźć ciąg
, który NIE jest słabo
domknięty. Wtedy można znaleźć ciąg
![]() taki, że
taki, że
![]() .
.
![]() jest
liniowym, ciągłym funkcjonałem istniejącym na mocy
lematu Mazura 3.3, takim że zachodzi ostra
nierówność:
jest
liniowym, ciągłym funkcjonałem istniejącym na mocy
lematu Mazura 3.3, takim że zachodzi ostra
nierówność:
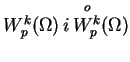 są refleksywne, a
są refleksywne, a
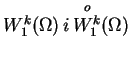 nie.
nie.
![]() Niech
Niech
![]() jest słabo
semi-ciągłym fynkcjonałem. Niech
jest słabo
semi-ciągłym fynkcjonałem. Niech
![]() oraz
oraz
![]() . Wtedy
oczywiście, na mocy definicji
. Wtedy
oczywiście, na mocy definicji
![]() jest słabo domknięty,
jeśli jest domknięty i wypukły, co mamy na mocy Twierdzenia
jest słabo domknięty,
jeśli jest domknięty i wypukły, co mamy na mocy Twierdzenia
![]()