



Next: Programowanie wypukłe. Wstęp.
Up: Programowanie matematyczne i układy
Previous: Punkty skrajne.
Spis rzeczy
6.1
Własności geometryczne. Niech
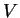
będzie przestrzenią
wektorową rzeczywistą oraz
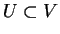
będzie jej
wektorową przestrzenią. Połóżmy
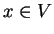
i niech
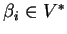
,
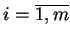
,
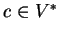
będą funkcjonałami liniowymi, ograniczonymi na
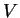
, oraz liczby
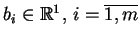
.
Następny problem, właśnie jego rozwiązanie :
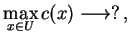 |
(6.1) |
gdzie dla
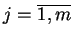
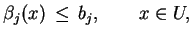 |
(6.2) |
nazywamy
programowaniem liniowym .
Następne twierdzenie daje geometryczne rozwiązanie problemu
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), (
), (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
6.2
Twierdzenie Niech
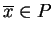
, gdzie
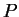
jest poliedrem zdefiniowanym przez (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
). Wtedy punkt
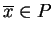
jest rozwiązaniem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
), gdy
zachodzi taka równość:
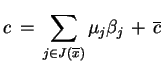 |
(6.3) |
dla niektórych
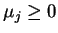
,
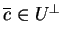
, gdzie
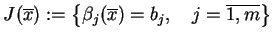
,
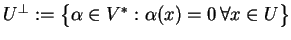
Dowód będzie wnioskiem z własności problemu dualnego do
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), (
), (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
6.3
Definicja. Punkt

będziemy nazywać
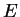
-punktem, gdy zachodzi taka własność:
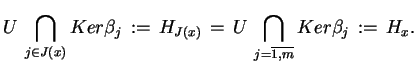 |
(6.4) |
6.4
Definicja. 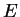
-punkt

nazywamy
niezdegenerowanym, gdy zachodzi taka równość :
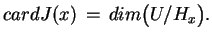 |
(6.5) |
6.5
Definicja. Poliedr 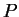
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy
prostym, gdy każdy
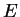
-punkt jest niezdegenerowany
Następne twierdzenie kojarzy 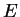 -punkty poliedra
-punkty poliedra 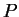 oraz jego
punkty skrajne.
oraz jego
punkty skrajne.
6.6
Twierdzenie. Niech poliedr
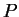
jest zdefiniowany przez
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
). Wtedy zbiór wszystkich
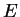
-punktów poliedra
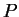
jest taki sam jak zbiór punktów skrajnych poliedra
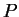
.
 Niech
Niech  będzie
będzie 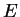 -punktem
-punktem 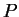 , oraz zachodzi
równość:
, oraz zachodzi
równość:
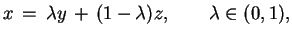 |
(6.6) |
gdzie 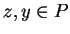 . Jest jasne, że mamy równość:
. Jest jasne, że mamy równość:
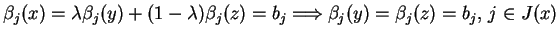 ,
,
ponieważ
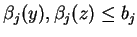 , oraz
, oraz
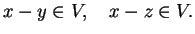 |
(6.7) |
Innymi słowy
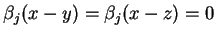 dla
wszystkich
dla
wszystkich 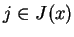 . Na mocy definicji (
. Na mocy definicji (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
mamy, że
ponieważ
)
mamy, że
ponieważ
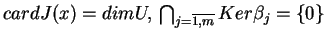 . Ostatnia równość oznacza, że poliedr
. Ostatnia równość oznacza, że poliedr 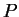 jest obszarem zwartym tj. ograniczonym, co zakładamy.
jest obszarem zwartym tj. ograniczonym, co zakładamy.
Stąd otrzymujemy, że ograniczenia funkcjonałów
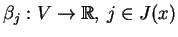 , na
, na 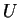 generują przestrzeń
generują przestrzeń 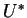 . To daje wtedy
oczywiście
. To daje wtedy
oczywiście
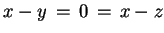 |
(6.8) |
Równości (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oznaczają, że
) oznaczają, że 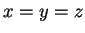 , tj.
punkt
, tj.
punkt  jest skrajnym!
jest skrajnym!
Odwrotnie, gdy  jest punktem skrajnym poliedra
jest punktem skrajnym poliedra 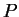 ,
wtedy istnieje punkt
,
wtedy istnieje punkt 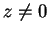 ,
,
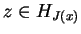 ,
jeśli
,
jeśli
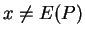 ! Jasne, że
oraz punkty
! Jasne, że
oraz punkty
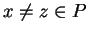 , co jest sprzeczym z
założeniem skrajności punktu
, co jest sprzeczym z
założeniem skrajności punktu  , to znaczy, że
, to znaczy, że
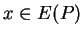 i
i
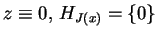 co dowodzi
twierdzenie
co dowodzi
twierdzenie 
6.7
Uwaga Wyżej w postaci uwikłanej skorzystaliśmy z
takiego twierdzenia.
6.8
Twierdzenie Wypukły poliedr
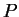
dla układu
nierówności
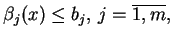 |
(6.9) |
gdzie
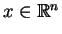
, może być przedstawiony w
postaci
gdzie
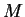
jest ograniczonym wielościanem w
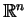
oraz
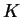
jest wypukłym stożkiem
wielościennym, złożonym z rozwiązań odpowiedniego układu
nierówności jednorodnych:
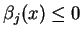
,
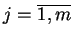
.
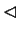 Rozważmy odpowiedni do (
Rozważmy odpowiedni do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) następny układ
nierówności
) następny układ
nierówności
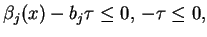 |
(6.10) |
gdzie
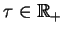 jest nową współrzędną,
wspólnie ze zmiennymi
jest nową współrzędną,
wspólnie ze zmiennymi
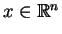 . Jest
oczywistym, że układ (
. Jest
oczywistym, że układ (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) wydziela w przestrzeni
) wydziela w przestrzeni
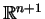 zbiór -
zbiór - 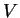 -stożek rozwiązań
-stożek rozwiązań
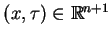 . Niech teraz stożek
. Niech teraz stożek
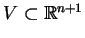 jest przecięty
hiperpłaszczyzną o równaniu
jest przecięty
hiperpłaszczyzną o równaniu 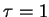 .
.
Jeżeli
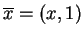 należy tej warstwie przekroju
należy tej warstwie przekroju
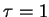 , to
, to  . Odwrotnie, jeżeli
. Odwrotnie, jeżeli
 , to
, to
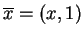 należy do
przekroju stożka
należy do
przekroju stożka 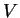 .
.
Wypukły stożek 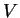 jest wielościenny to znaczy jezt złożony z wypukłych kombinacji
skończonego zbioru punktów. Ponieważ dla wszystkich
punktów jego ostatnia współrzędna jest
jest wielościenny to znaczy jezt złożony z wypukłych kombinacji
skończonego zbioru punktów. Ponieważ dla wszystkich
punktów jego ostatnia współrzędna jest
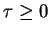 ,
to tworzące elementy tego stożka są dwóch rodzajów:
,
to tworzące elementy tego stożka są dwóch rodzajów:
-
-
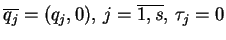 |
(6.11) |
Punkty rodzaju 1) będą istnieć koniecznie, ponieważ
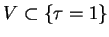 . Oczywi-ście, można uważać,
że wszystkie
. Oczywi-ście, można uważać,
że wszystkie
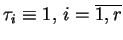 ,
skalując punkty z 1).
,
skalując punkty z 1).
Tak więc, każdy punkt
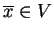 ma następującą
reprezentację:
ma następującą
reprezentację:
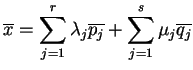 |
(6.12) |
Na hiperpłaszczyźnie
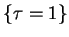 są tylko punkty
są tylko punkty
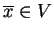 dla których, oczywiście
dla których, oczywiście
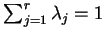 . To zanczy, że poliedr
. To zanczy, że poliedr 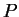 jest wyczerpany wszystkimi możliwymi kombinacjami typu
jest wyczerpany wszystkimi możliwymi kombinacjami typu
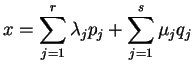 |
(6.13) |
gdzie
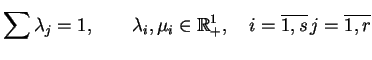 |
(6.14) |
Zbiór punktów
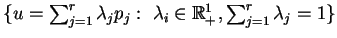 tworzy wypukły wielo-ścian
tworzy wypukły wielo-ścian
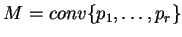 , a punkty
, a punkty
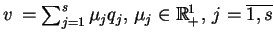 , tworzą
wypukły stożek
, tworzą
wypukły stożek
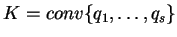 . Tak więc,
otrzymaliśmy poszukiwane rozłożnie
. Tak więc,
otrzymaliśmy poszukiwane rozłożnie 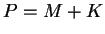

6.9
Twierdzenie (o istnieniu) Jeżeli zbiór wartości
dopuszczalnych problemu programowania liniowego
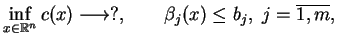 |
(6.15) |
jest niepusty oraz
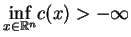
, wówczas rozwiązanie
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
istnieje.
 Dowód. Rozważmy zbiór
Dowód. Rozważmy zbiór
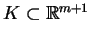 , złożony z
wektorów
, złożony z
wektorów
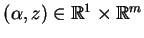 , takich że dla
każdego
, takich że dla
każdego
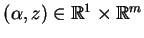 istnieje wektor
istnieje wektor
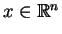 , taki że
, taki że
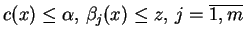 .
Oczywiście, że
.
Oczywiście, że 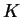 jest stożkiem.
jest stożkiem.
6.10
Lemat Stożek
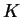
jest
skończenie zgenerowany.
Musimy pokazać, że
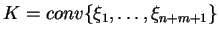 , gdzie
, gdzie
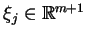 ,
,
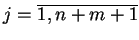 . Zdefiniujmy wektory:
. Zdefiniujmy wektory:
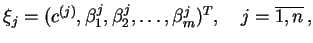 |
(6.16) |
Oczywiście, że wszystkie
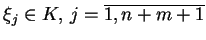 , tj
, tj
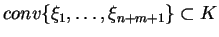 .
.
Niech teraz
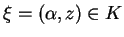 . Wtedy dla pewnego
. Wtedy dla pewnego
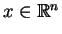 i niektórych
i niektórych
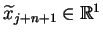 ,
,
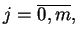 spełnione są relacje:
spełnione są relacje:
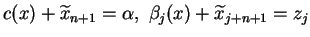 |
(6.17) |
dla
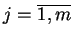 . Ale (
. Ale (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) dokładnie
oznacza że
) dokładnie
oznacza że
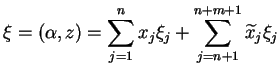 |
(6.18) |
tj.
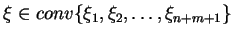 ,
albo
,
albo
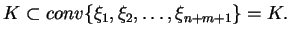 |
(6.19) |
6.11
Lemat Stożek
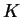
jest domknięty.
 Połóżmy teraz
Połóżmy teraz
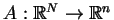 , gdzie
, gdzie
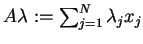 dla
dla
 ,
,
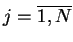 .
.
Oczywiście
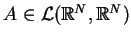 i obraz
i obraz
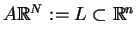 - skończenie
wymiarowa podprzestrzeń w
- skończenie
wymiarowa podprzestrzeń w
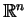 . Na mocy
Twierdzenia Banacha o operatorze odwrotnym, istnieje ograniczony
odwrotny operator
. Na mocy
Twierdzenia Banacha o operatorze odwrotnym, istnieje ograniczony
odwrotny operator
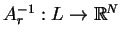 ,
taki że dla
,
taki że dla
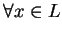
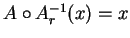 oraz
oraz
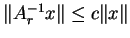 ,
, 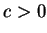 . Niech teraz
. Niech teraz
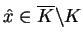 ,
,
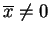 ; wtedy istnieje ciąg
; wtedy istnieje ciąg
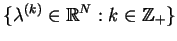 ,
taki, że
,
taki, że
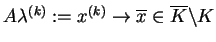 . Dalej, istnieje taka liczba
. Dalej, istnieje taka liczba
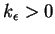 , że przy
, że przy
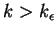 zachodzi
zachodzi
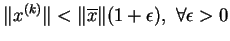 .
.
Ponieważ dla
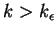
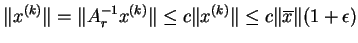 |
(6.20) |
ciąg
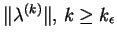 , jest
ograniczony, to można wybrać podciąg
, jest
ograniczony, to można wybrać podciąg
 taki, że
taki, że
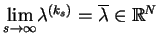 .
Dalej mamy: (ponieważ operator
.
Dalej mamy: (ponieważ operator  jest ciągły!)
jest ciągły!)
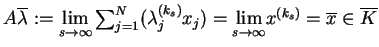 .
.
Ostatnia równość znaczy że
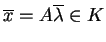 ,
tj. stożek
,
tj. stożek 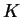 jest domknięty
jest domknięty 
Z warunku istnienia dopuszczalnego elementu
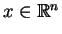 , istnieje element stożka
, istnieje element stożka 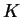 w
postaci
w
postaci
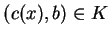 . Oprócz tego mamy, że
. Oprócz tego mamy, że
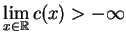 . To
znaczy w szczególności, że
. To
znaczy w szczególności, że
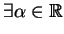 że
że
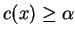 dla
dla
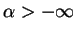 . Tak więc, zbiór
. Tak więc, zbiór
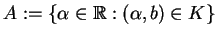 jest niepusty i
jest niepusty i
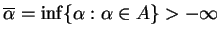 .
Stąd
.
Stąd
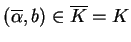 (lemat
(lemat
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), tj. istnieje taki element
), tj. istnieje taki element
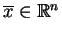 , dla którego
, dla którego
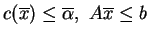 , co rozwiązuje problem (
, co rozwiązuje problem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
) 
6.12
Metoda simpleks - Algorytm rozwiązania problemu
kanonicznego
Problem kanoniczny ma postać:
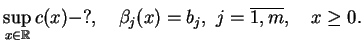 |
(6.21) |
Zdefiniujmy także:
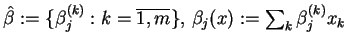 Krok 1
Krok 1 Znaleźć punkt skrajny
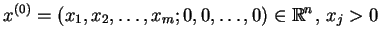
,
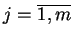
, ze zbioru elementów dopuszczalnych.
(Jak szukać
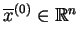
będzie
niżej powiedziane)
Krok 2 Zbudować simpleks - tablicę dla tego punktu
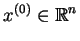
(P
ATRZ TABLICA)
Krok 3 Zbadać simpleks - tablicę:
- i)
- jeśli wszystkie
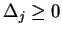 , to
, to
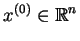 jest rozwiązaniem problemu (
jest rozwiązaniem problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
- ii)
- jeśli przy niektórym
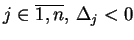 i
i
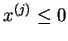 , to wartość problemu jest
, to wartość problemu jest
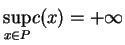 , gdzie
, gdzie
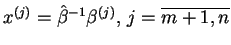 .
.
- iii)
- Niech w rzędzie
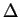 są ujemne liczby, a
odpowiednie kolumny
są ujemne liczby, a
odpowiednie kolumny 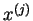 złożone z liczb dodatnich.
złożone z liczb dodatnich.
Połóżmy
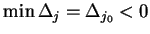 . Oczywiście że
. Oczywiście że
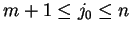 . kolumna z indeksem
. kolumna z indeksem 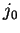 nazywana wtedy rozwiązywalną.
nazywana wtedy rozwiązywalną.
Jeśli
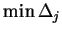
jest osiągalny przy kilku
wartościach

, to w jakości kolumny rozwiązywalnej wybieramy
dowolną z-taką samą wartością
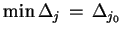
.
Oznaczmy
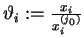
dla
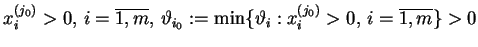
.
Wiersz wektora
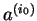
nazywany jest
rozwiązywalnym. (Jeśli
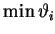
jest
osiągalny przy kilku indeksach
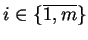
to
wybieramy dowolny wiersz odpowiedniego wektora.) Wtedy element
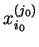
wektora
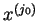
nazywany
jest
elementem rozwiązywalnym tablicy
.
| | |
| | 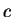 |
| | |
| | 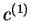 |
| | ... |
| | 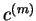 |
| | 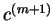 |
| | ... |
| |
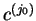 |
| | ... |
| | 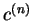 |
| | |
|
| | baza |
| | |
| | 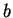 |
| |
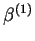 |
| | ... |
| |
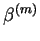 |
| |
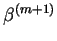 |
| | ... |
| |
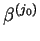 |
| | ... |
| |
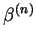 |
| | 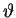 |
|
| | 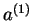 |
| | 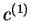 |
| | 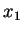 |
| | 1 |
| | ... |
| | 0 |
| |
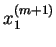 |
| | ... |
| |
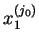 |
| | ... |
| |
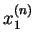 |
| |
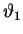 |
|
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
|
| |
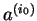 |
| |
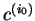 |
| | 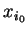 |
| | 0 |
| | ... |
| | 0 |
| |
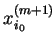 |
| | ... |
| |
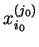 |
| | ... |
| |
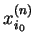 |
| |
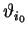 |
|
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
| | ... |
|
| | 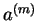 |
| | 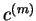 |
| | 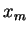 |
| | 0 |
| | ... |
| | 1 |
| |
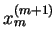 |
| | ... |
| |
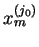 |
| | ... |
| |
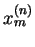 |
| |
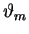 |
|
| | 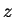 |
| | |
| |
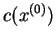 |
| | 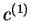 |
| | ... |
| | 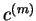 |
| |
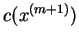 |
| | ... |
| |
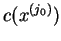 |
| | ... |
| |
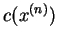 |
| | |
|
| |
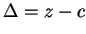 |
| | |
| | |
| | 0 |
| | ... |
| | 0 |
| |
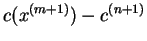 |
| | ... |
| |
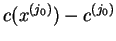 |
| | ... |
| |
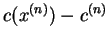 |
| | |
|
TABLICA 1
Dalej należy wyłączyć z wektorów bazowych wektor
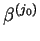 . Wartość funkcjnału na nowym punkcie
skrajnym
. Wartość funkcjnału na nowym punkcie
skrajnym
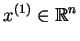 z nowymi numerami
bazowymi
z nowymi numerami
bazowymi
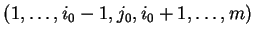 rośnie na
rośnie na
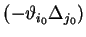 .
.
Krok 4 Zbudować nową tablicę simpleku dla nowej bazy
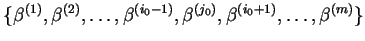 , tzn. mamy właściwie rozwinąć wektory
, tzn. mamy właściwie rozwinąć wektory
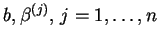 względem nowej bazy,
wymienionej wyżej.
względem nowej bazy,
wymienionej wyżej.
Nową tablicę simpleksu konstruujemy przy pomocy poprzedniej.
Elementy tablicy
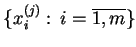 ,
,
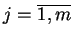 , stojące pod wektorami
, stojące pod wektorami
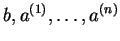 nie leżące w kolumnie
rozwiązywalnej lub w rozwiązywalnym wierszu poprzedniej tablicy
simpleksu mogą być wyliczone przy pomocy takiej reguły
prostokąta:
nie leżące w kolumnie
rozwiązywalnej lub w rozwiązywalnym wierszu poprzedniej tablicy
simpleksu mogą być wyliczone przy pomocy takiej reguły
prostokąta:
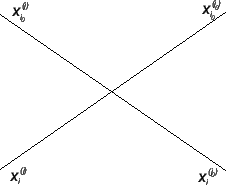
Rys. 1
|
z liczby
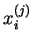
odjąć produkt
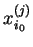
na
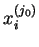
, podzielony
przez
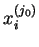
. Wtedy elementy wierrza
rozwiązywalnego mają postać:
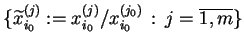
. Jest jasne, że w kolumnie
rozwiązywalnej
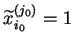
, a
reszta wartości równa zero. Dalej zaczynamy ponownie badać
tablicę simpleksu, otrzymaną wyżej.
6.13
Przykład Rozwiązać niezdegenerowany problem
programowania liniowego w postaci kanonicznej:
przy zadanym skrajnym punkcie
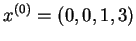
Rozwiązanie. Wektory bazowe
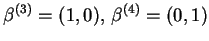 . Mamy tablicę
simpleksu:
. Mamy tablicę
simpleksu:
.
| |
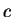 |
|
2 |
1 |
1 |
-1 |
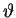 |
| |
|
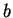 |
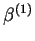 |
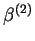 |
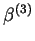 |
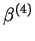 |
|
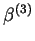 |
1 |
1 |
1 |
-1 |
1 |
0 |
|
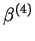 |
-1 |
3 |
2 |
1 |
0 |
1 |
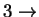 |
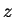 |
|
-2 |
-1 |
-2 |
1 |
-1 |
|
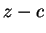 |
|
|
-3 |
-3 |
0 |
0 |
|
TABLICA 2
Z tablicy 2 widzimy, że w jakości kolumny rozwiązywalnej
można wziąść kolumny
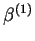 lub
lub
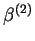 . Weźmy kolumnę
. Weźmy kolumnę
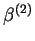 . Wtedy
mamy
. Wtedy
mamy
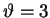 , a wiersz rozwiązywalny weźmy jako
, a wiersz rozwiązywalny weźmy jako
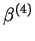 . Zmieniamy w bazie wektor
. Zmieniamy w bazie wektor
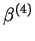 wektorem
wektorem
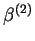 , i dla nowej
bazy konstuujemy nową tablicę simpleksu:
, i dla nowej
bazy konstuujemy nową tablicę simpleksu:
.
| |
c |
|
2 |
1 |
1 |
-1 |
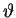 |
| baza |
|
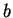 |
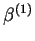 |
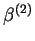 |
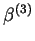 |
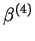 |
|
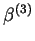 |
1 |
4 |
3 |
0 |
1 |
1 |
|
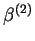 |
1 |
3 |
2 |
1 |
0 |
1 |
|
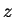 |
|
7 |
5 |
1 |
1 |
2 |
|
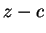 |
|
|
3 |
0 |
0 |
3 |
|
TABLICA 3
Widzimy z tablicy 3 że 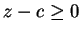 , tak więc punkt
, tak więc punkt
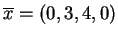 będzie rozwiąza-niem naszego
problemu, dając
będzie rozwiąza-niem naszego
problemu, dając
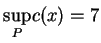 .
.
Aby uzasadnić metodę simpleks ważne są następujące
lematy.
6.14
Lemat Punkt dopuszczalny
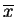
problemu
kanonicznego jest punktem skrajnym wtedy i tylko wtedy, gdy w
macierzy wektorów
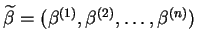
kolumny, odpowiadające niezerowym współrzędnym
wektora
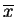
są liniowo niezależne
 Dowód niewprost.
Dowód niewprost.
Konieczność Niech
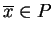 jest punktem
skrajnym. Przypuśćmy że odpowiednie kolumny macierzy
jest punktem
skrajnym. Przypuśćmy że odpowiednie kolumny macierzy
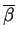 są liniowo zależne, tj. przy
są liniowo zależne, tj. przy
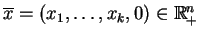 mamy równość:
tj.
mamy równość:
tj.
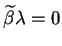 . Ponieważ wektor
. Ponieważ wektor
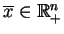 spełnia równanie
spełnia równanie
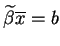 , otrzymujemy że
, otrzymujemy że
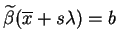 dla małych
dla małych
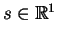 . To znaczy że wektor
. To znaczy że wektor
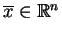 nie jest skrajnym. A to
znaczy, że wektory
nie jest skrajnym. A to
znaczy, że wektory
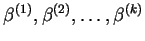 są niezależne.
są niezależne.
Teraz przypuśćmy, że
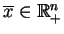 jest punktem
dopuszczalnym, oraz wektory
jest punktem
dopuszczalnym, oraz wektory
 , są liniowo niezależne. Przy warunku, że
, są liniowo niezależne. Przy warunku, że
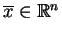 nie jest punktem
skrajnym, istnieją punkty
nie jest punktem
skrajnym, istnieją punkty
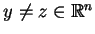 ,
takie że
,
takie że
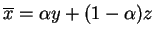 przy
niektórym
przy
niektórym
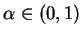 . Z tej równości widzimy, że
wektory
. Z tej równości widzimy, że
wektory 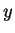 i
i
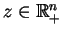 mają te same
niezerowe współrzędne co wektor
mają te same
niezerowe współrzędne co wektor
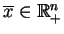 . Ponieważ
. Ponieważ
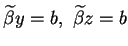 , to
, to
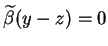 co oznacza, że
co oznacza, że
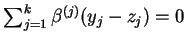 , tj. wektory
, tj. wektory
 , liniowo zależne co
zaprzecza założeniu. Tak więc
, liniowo zależne co
zaprzecza założeniu. Tak więc
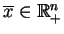 jest punktem skrajnym
jest punktem skrajnym

6.15
Lemat Dla problemu niezdegenerowanego kaźdy punkt
dopuszczalny ma nie mniej niż
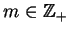
dodatnich współrzędnych.
 Dowód niewprost.
Dowód niewprost.
Przypuśćmy, że istnieje punkt dopuszczalny, który ma mniej
niż
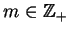 dodatnich współrzędnych. Dla
pewności będziemy uważać, że to pierwsze
dodatnich współrzędnych. Dla
pewności będziemy uważać, że to pierwsze 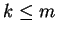 współrzędne. Rozważmy zbiór
współrzędne. Rozważmy zbiór
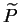 rozwiązań
układu
rozwiązań
układu
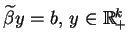 ,
gdzie
,
gdzie
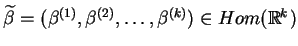 .
.
Niech
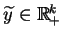 jest punktem
skrajnym zbioru
jest punktem
skrajnym zbioru
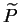 , który oczywiście istnieje.
Wtedy oczywiście punkt
, który oczywiście istnieje.
Wtedy oczywiście punkt
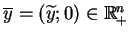 jest
punktem skrajnym zbioru
jest
punktem skrajnym zbioru 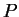 , u którego mniej niż
, u którego mniej niż
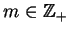 dodatnich wspólrzędnych. Ostatecznie
sprzeczne z niezdegenerowalnością problemu
dodatnich wspólrzędnych. Ostatecznie
sprzeczne z niezdegenerowalnością problemu 
6.16
Wniosek Dla problemu niezdegenrowanego punkt dopuszczalny
ma dokładnie
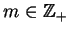
dodatnich
współrzędnych wtedy i tylko wtedy, gdy ten punkt jest punktem
skrajnym zbioru
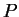
punktów dopuszczalnych.
Następne twierdzenie uzasadnia metodę simpleks.
DODATEK
Według dowodu H. Bresisa: Ponieważ zbiory
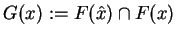 są wszystkie zwarte, to dla
dowodu tego że
są wszystkie zwarte, to dla
dowodu tego że
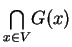 jest
niepuste, wystarczy pokazać, że rodzina
jest
niepuste, wystarczy pokazać, że rodzina
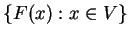 posiada własność przecięcia skończonego: dla wszystkich
podzbiorów skończonych
posiada własność przecięcia skończonego: dla wszystkich
podzbiorów skończonych
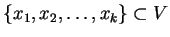 przecięcie
przecięcie
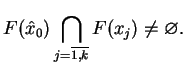 |
(6.23) |
Przypuśćmy, że (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) nie spełniono, tj. istnieje
podzbiór
) nie spełniono, tj. istnieje
podzbiór
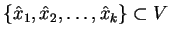 , że
, że
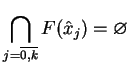 |
(6.24) |
Jeżeli
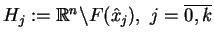 , wtedy oczywiście
, wtedy oczywiście
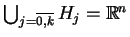 (!)
(!)
Weźmy teraz rozbicie jedynki
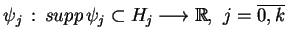 , skojarzone z otwrtym pokryciem
, skojarzone z otwrtym pokryciem
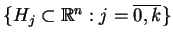 , tj.
takie, że
Rozważmy teraz takie odwzorowanie
, tj.
takie, że
Rozważmy teraz takie odwzorowanie
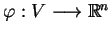 : dla każdego
: dla każdego
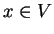
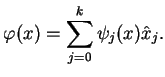 |
(6.25) |
Oczywiście
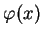 należy do powłoki wypukłej
należy do powłoki wypukłej 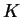 punktów
punktów
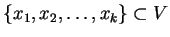 oraz
odwzorowuje
oraz
odwzorowuje 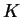 w siebie. Na mocy twierdzenia Brauera o punkcie
stałym istnieje punkt
w siebie. Na mocy twierdzenia Brauera o punkcie
stałym istnieje punkt
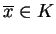 , taki że
, taki że
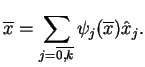 |
(6.26) |
Rozważmy wartości
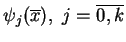 ,
(ponumerowane we właściwy sposób):
,
(ponumerowane we właściwy sposób):
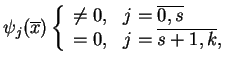 |
(6.27) |
tak więc punkt
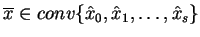 . Ponieważ
na mocy naszych założeń
. Ponieważ
na mocy naszych założeń
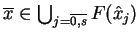 ,
co znaczy że
,
co znaczy że
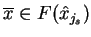 dla
pewnego
dla
pewnego
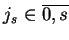 . Wtedy
. Wtedy
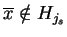 , tj.
, tj.
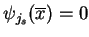 , co zaprzecza
(
, co zaprzecza
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Tym samym
). Tym samym
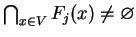 , co potrzebne było udowodnić
, co potrzebne było udowodnić 
6.19
Twierdzenie (Brauera F.) Niech
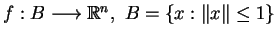
,
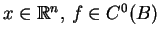
oraz
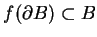
. Wtedy
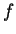
ma punkt stały.
 Rozważmy odwzorowanie
Rozważmy odwzorowanie
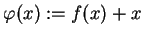 i jego
wartości na
i jego
wartości na
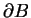 . Przypuszczamy, że
. Przypuszczamy, że
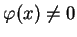 na
na
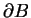 . Wtedy wektor
. Wtedy wektor
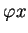 nie będzie się nigdzie równał zeru na
brzegu
nie będzie się nigdzie równał zeru na
brzegu
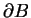 , skąd widizmy że dla każdego
elementu
, skąd widizmy że dla każdego
elementu
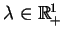 będzie zachodzić
nierówność. Dla
będzie zachodzić
nierówność. Dla
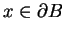
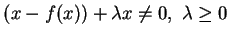 |
(6.28) |
albo
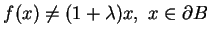 |
(6.29) |
Rzeczywiście, niech przy
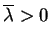 będzie w
(
będzie w
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) równość, tj.
) równość, tj.
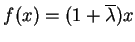 ,
,
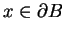 ,
co znaczy, że
,
co znaczy, że
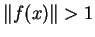 co jest sprzeczne z warunkiem
co jest sprzeczne z warunkiem
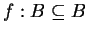 , skąd
, skąd
 . Tym samym
(
. Tym samym
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) zachodzi dla wszystkich
) zachodzi dla wszystkich
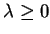 .
Wyliczając indeks
.
Wyliczając indeks
![$ deg(\varphi,B;0)=deg(\varphi_{t},B;0)\Big\vert _{t\in[0,1]}\Longrightarrow
\\...
...ghtarrow deg(I,B;0)=1\,, \varphi_{t}(x)=t\varphi(x)\,+\,(1-t)x,\,\,
t\in[0,1],$](img667.gif) otrzymujemy, że istnieje punkt
otrzymujemy, że istnieje punkt
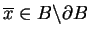 , taki, że
, taki, że
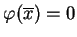 albo
albo
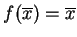 , tj. punkt stały w
, tj. punkt stały w 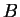 .
.





Next: Programowanie wypukłe. Wstęp.
Up: Programowanie matematyczne i układy
Previous: Punkty skrajne.
Spis rzeczy
![]() Niech
Niech ![]() będzie
będzie ![]() -punktem
-punktem ![]() , oraz zachodzi
równość:
, oraz zachodzi
równość:
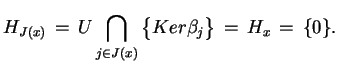
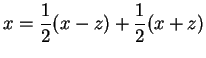
![]() Rozważmy odpowiedni do (
Rozważmy odpowiedni do (![]() ) następny układ
nierówności
) następny układ
nierówności
![]() należy tej warstwie przekroju
należy tej warstwie przekroju
![]() , to
, to ![]() . Odwrotnie, jeżeli
. Odwrotnie, jeżeli
![]() , to
, to
![]() należy do
przekroju stożka
należy do
przekroju stożka ![]() .
.
![]() jest wielościenny to znaczy jezt złożony z wypukłych kombinacji
skończonego zbioru punktów. Ponieważ dla wszystkich
punktów jego ostatnia współrzędna jest
jest wielościenny to znaczy jezt złożony z wypukłych kombinacji
skończonego zbioru punktów. Ponieważ dla wszystkich
punktów jego ostatnia współrzędna jest
![]() ,
to tworzące elementy tego stożka są dwóch rodzajów:
,
to tworzące elementy tego stożka są dwóch rodzajów:
![]() ma następującą
reprezentację:
ma następującą
reprezentację:
![]() Dowód. Rozważmy zbiór
Dowód. Rozważmy zbiór
![]() , złożony z
wektorów
, złożony z
wektorów
![]() , takich że dla
każdego
, takich że dla
każdego
![]() istnieje wektor
istnieje wektor
![]() , taki że
, taki że
![]() .
Oczywiście, że
.
Oczywiście, że ![]() jest stożkiem.
jest stożkiem.
![]() Połóżmy teraz
Połóżmy teraz
![]() , gdzie
, gdzie
![]() dla
dla
![]() ,
,
![]() .
.
![]() i obraz
i obraz
![]() - skończenie
wymiarowa podprzestrzeń w
- skończenie
wymiarowa podprzestrzeń w
![]() . Na mocy
Twierdzenia Banacha o operatorze odwrotnym, istnieje ograniczony
odwrotny operator
. Na mocy
Twierdzenia Banacha o operatorze odwrotnym, istnieje ograniczony
odwrotny operator
![]() ,
taki że dla
,
taki że dla
![]()
![]() oraz
oraz
![]() ,
, ![]() . Niech teraz
. Niech teraz
![]() ,
,
![]() ; wtedy istnieje ciąg
; wtedy istnieje ciąg
![]() ,
taki, że
,
taki, że
![]() . Dalej, istnieje taka liczba
. Dalej, istnieje taka liczba
![]() , że przy
, że przy
![]() zachodzi
zachodzi
![]() .
.
![]()
![]() ,
tj. stożek
,
tj. stożek ![]() jest domknięty
jest domknięty ![]()
![]() , istnieje element stożka
, istnieje element stożka ![]() w
postaci
w
postaci
![]() . Oprócz tego mamy, że
. Oprócz tego mamy, że
![]() . To
znaczy w szczególności, że
. To
znaczy w szczególności, że
![]() że
że
![]() dla
dla
![]() . Tak więc, zbiór
. Tak więc, zbiór
![]() jest niepusty i
jest niepusty i
![]() .
Stąd
.
Stąd
![]() (lemat
(lemat
![]() ), tj. istnieje taki element
), tj. istnieje taki element
![]() , dla którego
, dla którego
![]() , co rozwiązuje problem (
, co rozwiązuje problem (![]() )
) ![]()
![]() . Wartość funkcjnału na nowym punkcie
skrajnym
. Wartość funkcjnału na nowym punkcie
skrajnym
![]() z nowymi numerami
bazowymi
z nowymi numerami
bazowymi
![]() rośnie na
rośnie na
![]() .
.
![]() , tzn. mamy właściwie rozwinąć wektory
, tzn. mamy właściwie rozwinąć wektory
![]() względem nowej bazy,
wymienionej wyżej.
względem nowej bazy,
wymienionej wyżej.
![]() ,
,
![]() , stojące pod wektorami
, stojące pod wektorami
![]() nie leżące w kolumnie
rozwiązywalnej lub w rozwiązywalnym wierszu poprzedniej tablicy
simpleksu mogą być wyliczone przy pomocy takiej reguły
prostokąta:
nie leżące w kolumnie
rozwiązywalnej lub w rozwiązywalnym wierszu poprzedniej tablicy
simpleksu mogą być wyliczone przy pomocy takiej reguły
prostokąta:

![$ deg(\varphi,B;0)=deg(\varphi_{t},B;0)\Big\vert _{t\in[0,1]}\Longrightarrow
\\...
...ghtarrow deg(I,B;0)=1\,, \varphi_{t}(x)=t\varphi(x)\,+\,(1-t)x,\,\,
t\in[0,1],$](img667.gif) otrzymujemy, że istnieje punkt
otrzymujemy, że istnieje punkt