



Next: Programowanie wypukłe. Zagadnienia związane
Up: Programowanie matematyczne i układy
Previous: Programowanie Liniowe i Metoda
Spis rzeczy
Niech
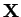 jest przestrzenią liniową, a f - zadaną
funkcją
jest przestrzenią liniową, a f - zadaną
funkcją
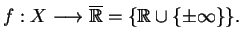 |
(7.1) |
Z każdą taką funkcją można skojarzyć takie dwa zbiory:
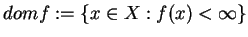 - tzw. zbiór efektywny ,
- tzw. zbiór efektywny ,
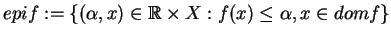 -
nadwykres.
-
nadwykres.
Funkcja
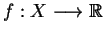 nazywa się własną, jeżeli
nazywa się własną, jeżeli
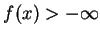 dla
dla
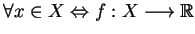 przy
przy
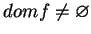 .
.
Oczywiście, funkcja
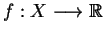 jest wypukła wtedy i tylko wtedy,
kiedy
jest wypukła wtedy i tylko wtedy,
kiedy
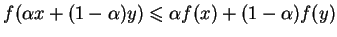 |
(7.2) |
dla
![$ \forall\: x, y \in X, \alpha\in[0,1]$](img680.gif)
Nierówność (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) nazywa się nierównością Jensena.
) nazywa się nierównością Jensena.
7.1
Twierdzenie Minkowskiego (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
) Zwarty zbiór w
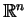
jest wypukłą powłoką swoich punktów
skrajnych.
Mamy działania nad zbiorami:
- 1)
- suma :
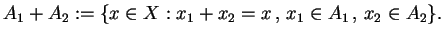
- 2)
- konwolucja :
![$ A_{1}\,\blacklozenge\, A_{2}:=\bigcup\{\alpha A_{1}\bigcap
(1-\alpha)A_{2}\, :\, \alpha\in[0,1]\}.$](img682.gif)
- 3)
- przecięcie :
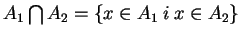 .
.
- 4)
- wypukła powłoka lub łączność wypukła nad
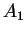 i
i 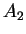 :
:
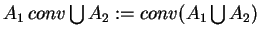 .
.
7.2
Definicja Transformacją lub sprzężeniem
Legendre'a-Young'a-Fenchela funkcji
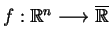
nazywamy odwzorowanie:
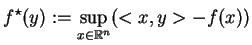 |
(7.3) |
gdzie funkcja
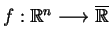
jest dowolna.
Z definicji ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) widać, że
widać, że
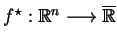 jest górną obwiednią rodziny funkcji
afinicznych, tj.
jest górną obwiednią rodziny funkcji
afinicznych, tj.
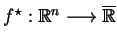 jest wypukła.
jest wypukła.
Odpowiednio, funkcja
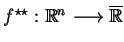 , gdzie
, gdzie
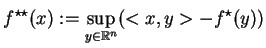 |
(7.4) |
nazywa się drugim skojarzeniem lub sprzężeniem L-Y-F do funkcji
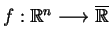 .
.
Z samej definicji ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) oraz (
oraz (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy, że:
) otrzymujemy, że:
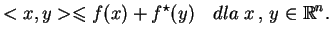 |
(7.5) |
7.3
Przykład. Weźmy
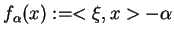
,
gdzie
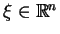
oraz
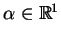
są zadane. Wtedy, oczywiście, na
mocy (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
otrzymujemy, że:

, jeśli
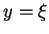
i
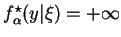
, jeśli
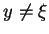
.
Łatwo wykazać, że
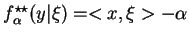
.
Niech teraz
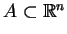 jest zbiorem niepustym.
jest zbiorem niepustym.
7.4
Definicja. Polarą zbioru
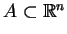
nazywamy zbiór:
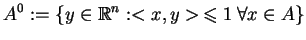 |
(7.6) |
Zbiór
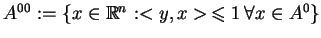
nazywamy
bipolarą zbioru

.
Z samej definicji ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) widzimy, że
widzimy, że 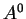 jest
przecięciem rodziny semiprzestrzeni
zawierających zero, tj. wypukły zbiór z zerem.
jest
przecięciem rodziny semiprzestrzeni
zawierających zero, tj. wypukły zbiór z zerem.
7.5
Przykłady. Polarą odcinka
![$ [0,x]\subset\mathbb{R}^n$](img705.gif)
jest półpłaszczyzna
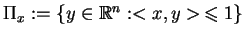
, i
odwrotnie
![$ \Pi_{x}^0=[0,x]$](img707.gif)
. Polarą kuli
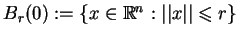
jest kula
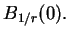
Niech
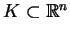 jest stożkiem w
jest stożkiem w
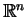 .
.
7.6
Definicja. Stożkiem
sprzężonym do stoźka
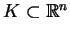
nazywamy zbiór:
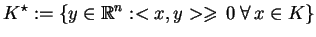 |
(7.7) |
Odpowiednio, stożek
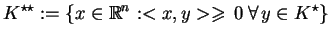 |
(7.8) |
nazywamy
drugim sprzężeniem do stożka
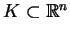
.
Na mocy definicji (7.7) widzimy od razu, że 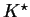 jest zbiorem wypukłym, domkniętym. Poza tym mamy następującą
właściwość:
jest zbiorem wypukłym, domkniętym. Poza tym mamy następującą
właściwość:
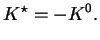 |
(7.9) |
7.7
Definicja. Subpochodną funkcji subliniowej
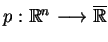
nazywamy zbiór:
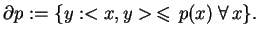 |
(7.10) |
Norma 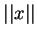 jest, oczywiście, funkcją subliniową.
Korzystając z (
jest, oczywiście, funkcją subliniową.
Korzystając z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
otzrymujemy, że:
)
otzrymujemy, że:
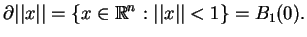 |
(7.11) |
7.8
Definicja. Subpochodną funkcji (wypukłej własnej) w
punkcie
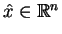
nazywamy zbiór:
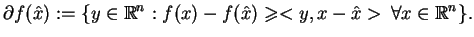 |
(7.12) |
Od razu widać, że
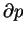 oraz
oraz
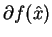 są zbiorami wypukłymi w
są zbiorami wypukłymi w
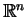 . Są
one również domknięte.
. Są
one również domknięte.
Niech teraz
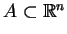 jest niepustym (!) podzbiorem
jest niepustym (!) podzbiorem
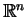
7.9
Definicja. Funkcję
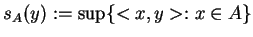 |
(7.13) |
nazywamy
,,oporną'' dla
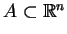
.
Oczywiście subpochodną funkcji liniowej
 jest punkt
jest punkt
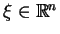 . Oporną funkcją elementu
. Oporną funkcją elementu
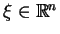 jest funkcja liniowa
jest funkcja liniowa
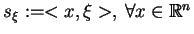 .
.
7.10
Definicja. Funkcja
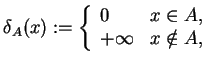 |
(7.14) |
nazywa się
indykatorem lub
wskaźnikiem zbioru
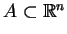
.
7.11
Przykład. Funkcją Minkowskiego kuli
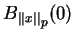
w
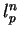
jest normą
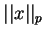
w
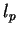
:
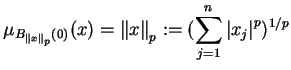 |
(7.15) |
gdzie
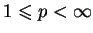
. Jeśli
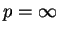
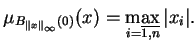 |
(7.16) |
Przejdźmy teraz do własności dwoistości lub
dualności obiektów wypukłych w
 .
.
7.12
Twierdzenie
- a)
- Funkcja
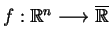 równa się
swojemu drugiemu sprzężeniu
równa się
swojemu drugiemu sprzężeniu
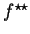 wg. L-Y-F
wtedy i tylko wtedy, gdy ona jest wypukła i domknięta (tj. jej
nadwykres jest zbiorem domkniętym i wypukłym).
wg. L-Y-F
wtedy i tylko wtedy, gdy ona jest wypukła i domknięta (tj. jej
nadwykres jest zbiorem domkniętym i wypukłym).
- b)
- Niech
 jest niepustym zbiorem w
jest niepustym zbiorem w
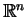 . Wtedy
. Wtedy 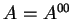 wtedy
i tylko wtedy, kiedy
wtedy
i tylko wtedy, kiedy  jest wypukłym, domkniętym zbiorem,
zawierającym zero.
jest wypukłym, domkniętym zbiorem,
zawierającym zero.
- c)
- Stożek
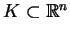 równa się
równa się
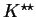 wtedy i tylko
wtedy, kiedy jest stożkiem wypukłym i domkniętym.
wtedy i tylko
wtedy, kiedy jest stożkiem wypukłym i domkniętym.
- d)
- Niech
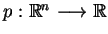 jest funkcją jednorodną
pierwszego stopnia z subpochodną
jest funkcją jednorodną
pierwszego stopnia z subpochodną
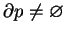 . Żeby była spełniona
równość
. Żeby była spełniona
równość
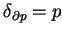 , jest koniecznym i wystarczającym, żeby funkcja
, jest koniecznym i wystarczającym, żeby funkcja
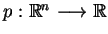 była
subliniowa i domknięta.
była
subliniowa i domknięta.
- e)
- Niech
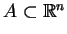 jest niepustym podzbiorem
jest niepustym podzbiorem
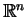 .
Żeby zachodziła równość
.
Żeby zachodziła równość
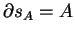 jest koniecznym i wystarczającym,
żeby zbiór
jest koniecznym i wystarczającym,
żeby zbiór
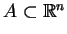 był domknięty i
wypukły.
był domknięty i
wypukły.
7.13
Uwaga. Twierdzenie (a) w
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
często nazywa
się
twierdzeniem Fenchela
- Moro.
 Dowód Twierdzenia
Dowód Twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) (b). Na mocy definicji mamy, że:
(b). Na mocy definicji mamy, że:
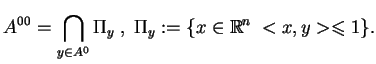 |
(7.17) |
Jeżeli 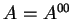 , to
, to  jest oczywiście zbiorem
wypukłym, domkniętym i zawierającym zero.
jest oczywiście zbiorem
wypukłym, domkniętym i zawierającym zero.
W drugą stronę mamy: jeśli  ,
,
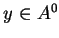 , to z definicji wynika, że
, to z definicji wynika, że
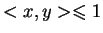 , tj.
, tj.
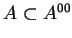 . Załóżmy, że
istnieje element
. Załóżmy, że
istnieje element
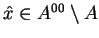 . Wtedy, na
mocy tego, że
. Wtedy, na
mocy tego, że  jest zbiorem domkniętym i wypukłym, z
twierdzenia o oddzielaniu można znaleźć taki element
jest zbiorem domkniętym i wypukłym, z
twierdzenia o oddzielaniu można znaleźć taki element
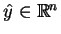 , że
, że
 |
(7.18) |
Z tego, że
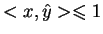 dla wszystkich
dla wszystkich
 , z (
, z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy, że
) otrzymujemy, że
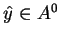 . Z drugiej nierówności otrzymujemy
także, że
. Z drugiej nierówności otrzymujemy
także, że
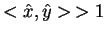 , co przeczy
założeniu, że
, co przeczy
założeniu, że
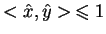 ,
ponieważ
,
ponieważ
 .
. 
Następne twierdzenie ma szerokie zastosowania (podamy bez dowodu).
7.14
Twierdzenie o zwartości.
- a)
- Niech
 jest otwartym otoczeniem zera w
jest otwartym otoczeniem zera w
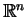 . Wtedy jego polara
jest zwarta.
. Wtedy jego polara
jest zwarta.
- b)
- Niech
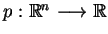 jest ciągłą subliniową funkcją
na
jest ciągłą subliniową funkcją
na
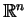 . Wtedy jej subpochodna
. Wtedy jej subpochodna
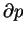 jest zbiorem wypukłym i zwartym.
jest zbiorem wypukłym i zwartym.
- c)
- Jeśli
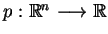 jest subliniową funkcją
domkniętą, to
jest subliniową funkcją
domkniętą, to
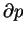 jest zbiorem domkniętym
wypukłym.
jest zbiorem domkniętym
wypukłym.




Next: Programowanie wypukłe. Zagadnienia związane
Up: Programowanie matematyczne i układy
Previous: Programowanie Liniowe i Metoda
Spis rzeczy
![]() , gdzie
, gdzie
![]() oraz (
oraz (![]() ) otrzymujemy, że:
) otrzymujemy, że:
![]() jest zbiorem niepustym.
jest zbiorem niepustym.
![]() jest niepustym (!) podzbiorem
jest niepustym (!) podzbiorem
![]()