


Next: Równanie dyfuzji
Up: Zagadnienie fizyczne i równania
Previous: Zagadnienie fizyczne i równania
Rozważmy jednorodne środowisko które zajmuje obszar
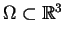 . Niech
. Niech
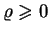 będzie jego
gęstością,
będzie jego
gęstością, 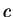 będzie jego cieplną pojemnością jednostki
masy środowiska. Przypuszczamy też, że wewnątrz środowiska
są źródła cieplne o gęstości f(x,t). Stawiamy problem
znalezienia temperatury środowiska u(t,x), gdzie
będzie jego cieplną pojemnością jednostki
masy środowiska. Przypuszczamy też, że wewnątrz środowiska
są źródła cieplne o gęstości f(x,t). Stawiamy problem
znalezienia temperatury środowiska u(t,x), gdzie
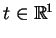 jest parametrem czasowym.
jest parametrem czasowym.
Niech objętość
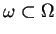 wewnątrz
środowiska ma wystarczająco gładki brzeg
wewnątrz
środowiska ma wystarczająco gładki brzeg
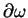 . Dla
zmiany temperatury
. Dla
zmiany temperatury
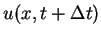 za czas
za czas
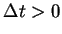 od
od 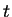 do
do
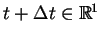 wewnątrz obszaru
wewnątrz obszaru
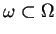 jest potrzebna następująca ilość ciepła
jest potrzebna następująca ilość ciepła
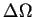 :
:
![$\displaystyle \Delta Q\,=\,\int_{\omega}c\varrho\big[u(x,t+\Delta
t)-u(x,t)\big]\,dx$](img535.gif) |
(5.1) |
Jedna jego część dostarcza się od źródeł wewnątrz
 :
:
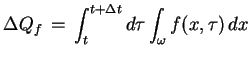 |
(5.2) |
a druga jego część dostarcza się przez brzeg
 , która na mocy prawa Fouriera równa się:
, która na mocy prawa Fouriera równa się:
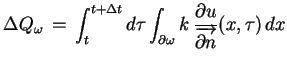 |
(5.3) |
gdzie k jest tzw. współczynnikiem przepływu
cieplnego,
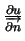 -
pochodna kierunkowa wzdłóż normali
-
pochodna kierunkowa wzdłóż normali
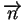 do
brzegu
do
brzegu
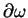 . Stąd otrzymujemy (z (5.1) i
(5.3)) że
. Stąd otrzymujemy (z (5.1) i
(5.3)) że
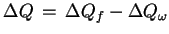 , tj.
, tj.
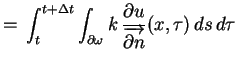 |
(5.4) |
Przypuszczając, że temperatura u(t,x)jest raz różniczkowalna
po
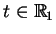 i dwa razy po
i dwa razy po
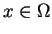 , a
funkcja
, a
funkcja 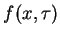 jest ciągła, znajdujemy:
jest ciągła, znajdujemy:
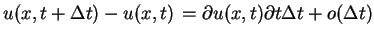 ,
,
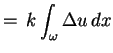 |
(5.5) |
gdzie skorzystaliśmy ze wzoru
Ostrogradskiego-Gaussa-Stokes'a :
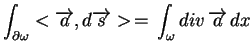 |
(5.6) |
Oprócz tego :
oraz
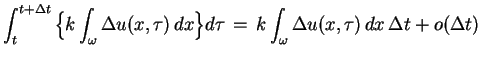 |
(5.7) |
Teraz równość (5.4) przyjmuje taką postać:
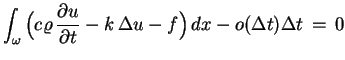 |
(5.8) |
Biorąc granicę wyrażenia (5.8) przy
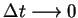 otrzymujemy :
otrzymujemy :
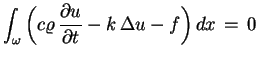 |
(5.9) |
Ponieważ równość (5.9) zachodzi dla wszystkich
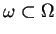 , a wyrażenie
, a wyrażenie
podcałkowe jest ciągłe,
to oczywiście
wewnątrz obszaru 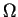 , lub
, lub
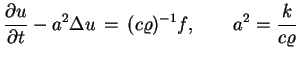 |
(5.10) |
tj. końcowe równania przepływu ciepła dla temperatury
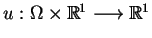 .
.
Analiza równań (5.10) oraz (5.4)
Jak widzieliśmy wyżej, równanie (5.10) zachodzi
wtedy i tylko wtedy, gdy źródło f(x,t) jest funkcją ciągłą
na
 . Na ogół tak nie jest,
oczywiście: ciepło może być emitowane w środowisko
. Na ogół tak nie jest,
oczywiście: ciepło może być emitowane w środowisko 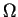 w
jakimś tylko punkcie
w
jakimś tylko punkcie
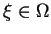 i być wszędzie
zerem, lub istnieć w okamgnieniu przy
i być wszędzie
zerem, lub istnieć w okamgnieniu przy
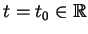 i być zerem przy
i być zerem przy
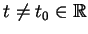 .
To znaczy, że mamy wrócić do podstawowej równości całkowej
(5.4) lub nauczyć się w sposób poprawny zrozumieć
równanie (5.10) i jego rozwiązania.
.
To znaczy, że mamy wrócić do podstawowej równości całkowej
(5.4) lub nauczyć się w sposób poprawny zrozumieć
równanie (5.10) i jego rozwiązania.
Drugie podejście okazało się bardziej pożyteczne.
Mianowicie, równanie (5.10) może być rozpatrzone jako
wyrażenie w uogólnionym sensie, tj. w sensie teorii dystrybucji:
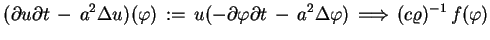 |
(5.11) |
gdzie
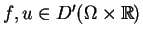 i
i
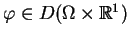 jest dowolna.
jest dowolna.
Niech
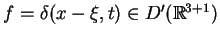 i
i
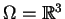 .
Wtedy oczywiście
.
Wtedy oczywiście
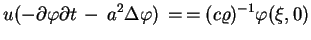 |
(5.12) |
dla każdej
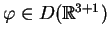 . Przy dodatkowym
założeniu takim,
. Przy dodatkowym
założeniu takim,
że
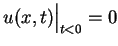 dla
wszystkich
dla
wszystkich
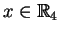 , można odzyskać dokładne
, można odzyskać dokładne
rozwiązanie dla
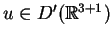 :
:
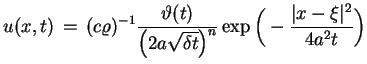 |
(5.13) |
dla wszystkich
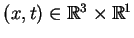 .
Wzór (5.13)opisuje temperaturę nieograniczonego
środowiska, która do wydzielenia przez źródło ciepł była
zerem.
.
Wzór (5.13)opisuje temperaturę nieograniczonego
środowiska, która do wydzielenia przez źródło ciepł była
zerem.



Next: Równanie dyfuzji
Up: Zagadnienie fizyczne i równania
Previous: Zagadnienie fizyczne i równania
Andrzej Janus Szef
2001-12-05
![]() . Niech
. Niech
![]() będzie jego
gęstością,
będzie jego
gęstością, ![]() będzie jego cieplną pojemnością jednostki
masy środowiska. Przypuszczamy też, że wewnątrz środowiska
są źródła cieplne o gęstości f(x,t). Stawiamy problem
znalezienia temperatury środowiska u(t,x), gdzie
będzie jego cieplną pojemnością jednostki
masy środowiska. Przypuszczamy też, że wewnątrz środowiska
są źródła cieplne o gęstości f(x,t). Stawiamy problem
znalezienia temperatury środowiska u(t,x), gdzie
![]() jest parametrem czasowym.
jest parametrem czasowym.
![]() wewnątrz
środowiska ma wystarczająco gładki brzeg
wewnątrz
środowiska ma wystarczająco gładki brzeg
![]() . Dla
zmiany temperatury
. Dla
zmiany temperatury
![]() za czas
za czas
![]() od
od ![]() do
do
![]() wewnątrz obszaru
wewnątrz obszaru
![]() jest potrzebna następująca ilość ciepła
jest potrzebna następująca ilość ciepła
![]() :
:
![$\displaystyle \int_{\omega}\big\{c\varrho\big[u(x,t+\Delta t)-u(x,t)\big]\,-\,
\int_{t}^{t+\Delta t}f(x,\tau)\,d\tau \big\}\,dx\,=
$](img542.gif)
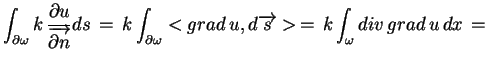
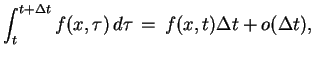
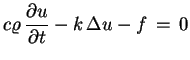
![]() . Na ogół tak nie jest,
oczywiście: ciepło może być emitowane w środowisko
. Na ogół tak nie jest,
oczywiście: ciepło może być emitowane w środowisko ![]() w
jakimś tylko punkcie
w
jakimś tylko punkcie
![]() i być wszędzie
zerem, lub istnieć w okamgnieniu przy
i być wszędzie
zerem, lub istnieć w okamgnieniu przy
![]() i być zerem przy
i być zerem przy
![]() .
To znaczy, że mamy wrócić do podstawowej równości całkowej
(5.4) lub nauczyć się w sposób poprawny zrozumieć
równanie (5.10) i jego rozwiązania.
.
To znaczy, że mamy wrócić do podstawowej równości całkowej
(5.4) lub nauczyć się w sposób poprawny zrozumieć
równanie (5.10) i jego rozwiązania.
![]() i
i
![]() .
Wtedy oczywiście
.
Wtedy oczywiście