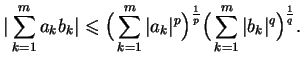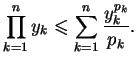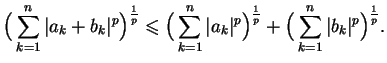Next: Funkcje uogólnione.
Up: Podstawowe pojęcia oraz przestrzenie
Previous: Podstawowe pojęcia oraz przestrzenie
Niech
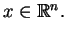 Wartość
Wartość
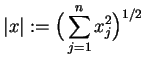 |
(1.1) |
jest jak wiadomo normą w
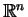 , którą nazywamy
euklidesową, ponieważ jest generowana przez iloczyn skalarny
, którą nazywamy
euklidesową, ponieważ jest generowana przez iloczyn skalarny
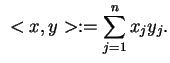 |
(1.2) |
Przestrzeń
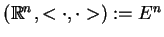 jest
najprostszym przykładem przestrzeni Hilberta.
Jednocześnie, definiując odleglość euklidesową w
jest
najprostszym przykładem przestrzeni Hilberta.
Jednocześnie, definiując odleglość euklidesową w 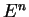
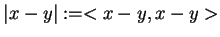 |
(1.3) |
nazywaną metryką, dostajemy przesrzeń metryczną  Z
drugiej strony norma (1.1) zadaje w
Z
drugiej strony norma (1.1) zadaje w  strukturę
przestrzeni Banacha ponieważ każdy ciąg podstawowy
strukturę
przestrzeni Banacha ponieważ każdy ciąg podstawowy
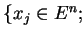
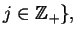 gdzie
gdzie
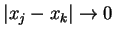
gdy
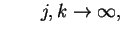
jest zbieżny do elementu
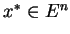 . To znaczy że
. To znaczy że
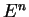 jest zupełną. Będziemy nazywać
jest zupełną. Będziemy nazywać
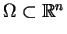 obszarem kiedy zbiór
obszarem kiedy zbiór 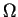 jest otwartym w
jest otwartym w
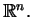 Domknięcie
Domknięcie
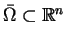 jest suma mnogościowa (brzegu )
jest suma mnogościowa (brzegu )
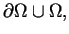 gdzie
gdzie
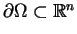 , jest brzegiem
zbioru
, jest brzegiem
zbioru 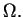 Obszar
Obszar
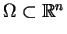 jest
ograniczony kiedy istnieje kula
jest
ograniczony kiedy istnieje kula
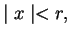 która
zawiera w sobie cały obszar
która
zawiera w sobie cały obszar 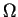 . Nam będą dalej potrzebne
różne klasy funkcji, określonych na
. Nam będą dalej potrzebne
różne klasy funkcji, określonych na 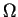 lub na
lub na
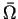 . Będziemy stosować oznaczenia L.Szwarca:
Niech
. Będziemy stosować oznaczenia L.Szwarca:
Niech 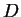 będzie ,,wektorem'' współrzędnych
będzie ,,wektorem'' współrzędnych
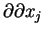 ,
,
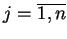 ,
,
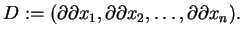 Będziemy nazywać wektor
Będziemy nazywać wektor
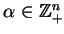 multiindeksem i połóżmy z definicji
multiindeksem i połóżmy z definicji
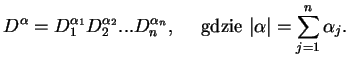 |
(1.4) |
Jeśli funkcja
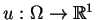 i ma
wystarczającą ilość pochodnych wtedy
i ma
wystarczającą ilość pochodnych wtedy
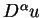 jest
pochodną rzędu
jest
pochodną rzędu 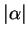 funkcji
funkcji
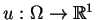 .
.
Przy pomocy powyższych oznaczeń jest prościej zapisywać
różne ogólne wyrażenia, zawierające pochodne. Na przykład,
równanie
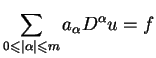 |
(1.5) |
reprezentuje sobą zwartą postać ogólnego wzoru dla liniowego
równania pochodnych cząstkowych rzędu
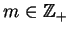 ze
współczynnikami
ze
współczynnikami
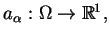
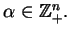
Zbiór funkcji skalarnych na 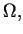 (zdefiniowanych na
(zdefiniowanych na 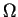 ) i mających
ciągłe pochodne łącznie do rzędu
) i mających
ciągłe pochodne łącznie do rzędu
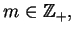 będziemy oznaczać
będziemy oznaczać
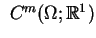 . Podzbiór
funkcji, które mają pochodne do rzędu
. Podzbiór
funkcji, które mają pochodne do rzędu
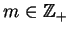 ciągłe na
ciągłe na
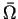 , jest oznaczany jako
, jest oznaczany jako
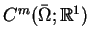 .
.
Teraz wprowadźmy pojęcie nośnika funkcji
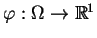 . Z defenicji, nośnik
. Z defenicji, nośnik 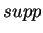
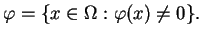 Nośnik
Nośnik 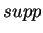
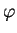 jest oczywiście zbiorem domkniętym. Przypomnijmy
także, że zbiór
jest oczywiście zbiorem domkniętym. Przypomnijmy
także, że zbiór
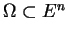 jest zwarty gdy
jest zwarty gdy 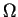 jest ograniczony i domknięty w
jest ograniczony i domknięty w 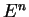 . Ważną klasą funkcij
są funkcje, których nośnik jest zwarty. To znaczy, że funkcja
z tej klasy jest tożsamościowo zerowa zewnątrz kuli
wystarczająco dużego promienia:
. Ważną klasą funkcij
są funkcje, których nośnik jest zwarty. To znaczy, że funkcja
z tej klasy jest tożsamościowo zerowa zewnątrz kuli
wystarczająco dużego promienia: 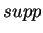
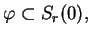
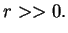
Podzbiór funkcji w
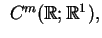 złożony z
funkcji ze zwartymi nośnikami, oznaczamy przez
złożony z
funkcji ze zwartymi nośnikami, oznaczamy przez
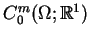 . Szczególnie interesujące są funkcje klasy
. Szczególnie interesujące są funkcje klasy
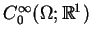 .
.
Jeśli
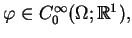 to
to
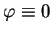 w niektórym paśmie około granicy.
w niektórym paśmie około granicy.
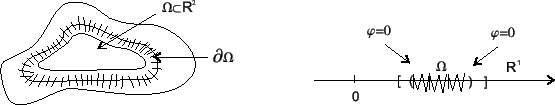
Rys. 1
|
Jeśli wziąć, na przykład, funkcję
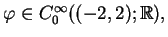 której nośnik
której nośnik
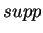
![$ \varphi
=[-1,1],$](img60.gif) to oczywiście, wszystkie pochodne w punkcie
to oczywiście, wszystkie pochodne w punkcie
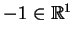 i pochodne w punkcie
i pochodne w punkcie
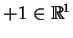 istnieją i są równe zero.
To znaczy że wykres funkcji
istnieją i są równe zero.
To znaczy że wykres funkcji
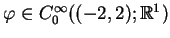 jest styczny z osią
jest styczny z osią
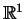 nieskonczonego rzędu. Powstaje pytanie, czy na ogół istnieją
takie funkcje? Gdy, naprzykład, funkcja
nieskonczonego rzędu. Powstaje pytanie, czy na ogół istnieją
takie funkcje? Gdy, naprzykład, funkcja
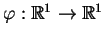 jest analityczna, to może ona nie
należeć do klasy
jest analityczna, to może ona nie
należeć do klasy
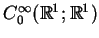 jeśli nie jest stałą tożsamościowo na
jeśli nie jest stałą tożsamościowo na
 .
Tym nie mniej, takie funkcji istnieją. Przykładem takiej funkcji
jest wyrażenie
.
Tym nie mniej, takie funkcji istnieją. Przykładem takiej funkcji
jest wyrażenie
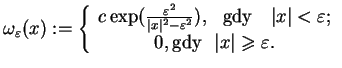 |
(1.6) |
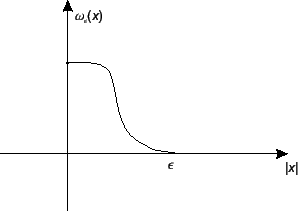
Rys. 2
|
Funkcję (1.6) nazywają czapeczką, jej nośnik 
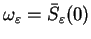 . Przy pomocy
tej funkcji (1.6) można konstruować inne funkcje klasy
. Przy pomocy
tej funkcji (1.6) można konstruować inne funkcje klasy
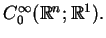 Poniżej przeliczymy podstawowe przestrzenie funkcyjne, które
bedziemy dalej wykorzystywać. We wszystkich tych przestrzeniach
będą określone pewne struktury metryczne lub topologiczne.
Rozważmy funkcjonały
Poniżej przeliczymy podstawowe przestrzenie funkcyjne, które
bedziemy dalej wykorzystywać. We wszystkich tych przestrzeniach
będą określone pewne struktury metryczne lub topologiczne.
Rozważmy funkcjonały
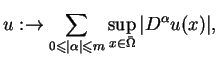 |
(1.7) |
one oczywiście są normami na przestrzeni liniowej
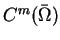 . Te normy są równoważne, a przestrzeń
. Te normy są równoważne, a przestrzeń
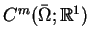 jest przestrzenią Banacha
względem norm (1.7).
Zbieżność
jest przestrzenią Banacha
względem norm (1.7).
Zbieżność
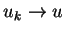 w sensie
w sensie
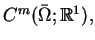 gdy
gdy
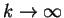 , jest zbieżnością
jednostajną w
, jest zbieżnością
jednostajną w 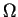 razem z pochodnymi do rzędu
razem z pochodnymi do rzędu
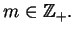 W przypadku gdy obszar
W przypadku gdy obszar
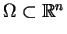 nie jest
ograniczony, normy (1.7) są niewystarczające żeby
przestrzen
nie jest
ograniczony, normy (1.7) są niewystarczające żeby
przestrzen
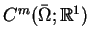 była
przestrzenią Banacha.
Wtedy zamiast (1.7) wprowadzmy rodzinę funkcjonałów
była
przestrzenią Banacha.
Wtedy zamiast (1.7) wprowadzmy rodzinę funkcjonałów
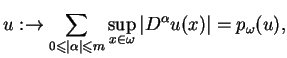 |
(1.8) |
gdzie
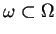 jest zwartym, ograniczonym
podzbiorem
jest zwartym, ograniczonym
podzbiorem 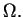 Funkcjonały (1.8) nazywamy
quasi-normami w
Funkcjonały (1.8) nazywamy
quasi-normami w
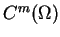 . Nazwijmy
. Nazwijmy
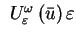 -otoczeniem elementu
-otoczeniem elementu
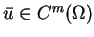 , jeśli istnieje taki zbiór
, jeśli istnieje taki zbiór
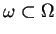 , że
, że
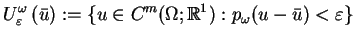 |
(1.9) |
W taki sposób skonstruowaliśmy przestrzeń topologiczną.
Zbieżność w tej przestrzeni oznacza, że
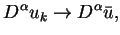 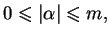 |
(1.10) |
na każdym zwartym podzbiorze
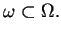
Twierdzenie 1.1
Przestrzeń
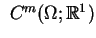
jako przestrzeń
topologiczna jest zupełną względem zbieżności
(
1.10), i tym samym jest przestrzenią Frechet'a, tj.
metryzowalną.
Następną przestrzenią będzie przestrzeń
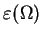 funkcji klasy
funkcji klasy
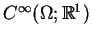 razem z
rodziną quasi-norm
razem z
rodziną quasi-norm
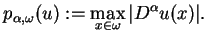 |
(1.11) |
Przestrzeń
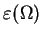 jest też przestrzenią
Frechet'a. Zbieżność w
jest też przestrzenią
Frechet'a. Zbieżność w
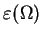 oznacza
oczywiście, zbieżność jednostajną
oznacza
oczywiście, zbieżność jednostajną
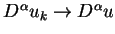 dla każdego
dla każdego
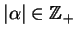 i na każdym zwartym podzbiorze
i na każdym zwartym podzbiorze
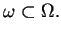 Przestrzeń
Przestrzeń
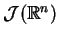 tworzą funkcje klasy
tworzą funkcje klasy
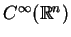 , wystarczająco szybko malejace przy
, wystarczająco szybko malejace przy
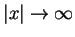 . To znaczy, że
. To znaczy, że
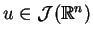 gdy dla wszystkich
gdy dla wszystkich
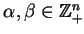 wartość
wartość
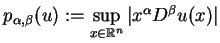 |
(1.12) |
jest ograniczona. Na przykład funkcja
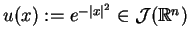 . Przestrzeń
. Przestrzeń
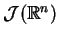 jest też przestrzenią Frechet'a.
Zbieżność
jest też przestrzenią Frechet'a.
Zbieżność
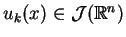 do zera
przy
do zera
przy
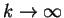 oznacza, że dla wszystkich
oznacza, że dla wszystkich
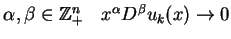 przy
przy
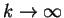 jednostojnie po
jednostojnie po
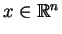 . Zachdzi wlasność:
. Zachdzi wlasność:
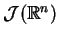
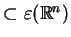 . (*)
. (*)
Przestrzeń
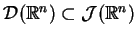 jest zbiórem funkcji klasy
jest zbiórem funkcji klasy
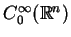 , tj.
, tj.
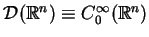 .
.
Przestrzeń
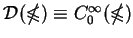 z topologią granicy indukcyjnej wszystkich
topologii (1.11) z różnymi
z topologią granicy indukcyjnej wszystkich
topologii (1.11) z różnymi
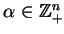 i
i
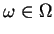 .
Mówimy, że ciąg
.
Mówimy, że ciąg
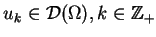 dąży do zera gdy
dąży do zera gdy
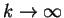 , w sensie
, w sensie
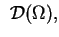 jeśli spełnione dwa warunki:
jeśli spełnione dwa warunki:
- i)
- istnieje zwarty podzbiór
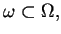 taki że
taki że
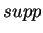
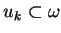 dla wszystkich
dla wszystkich
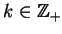 ;
;
- ii)
- ciąg
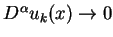 jednostajnie po
jednostajnie po
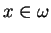 dla wszystkich
dla wszystkich
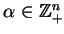 .
.
Zbieżność w
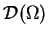 i odpowiednia topologia
była wprowadzona przez L.Schwarz'a w 1951r. Przestrzeń
i odpowiednia topologia
była wprowadzona przez L.Schwarz'a w 1951r. Przestrzeń
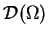 nie jest Frechetowską i nie jest
metryzowalną.
Oprócz przestrzeni wymienionych wyżej będziemy wykorzystywać
przestrzenie funkcji
nie jest Frechetowską i nie jest
metryzowalną.
Oprócz przestrzeni wymienionych wyżej będziemy wykorzystywać
przestrzenie funkcji
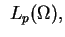
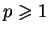 z normą
z normą
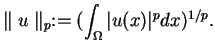 |
(1.13) |
Przestrzeń
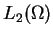 jest także przestrzenią Hilberta
względem iloczynu skalarnego
jest także przestrzenią Hilberta
względem iloczynu skalarnego
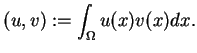 |
(1.14) |
Funkcje z
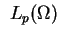 mają ważną własność lokalnej
całkowalności: dla każdego
mają ważną własność lokalnej
całkowalności: dla każdego
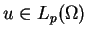 i każdego
zwartego podzbioru
i każdego
zwartego podzbioru
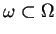 istnieje całka
istnieje całka
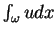 . Rzeczywiście, na mocy twierdzenia Holder'a:
. Rzeczywiście, na mocy twierdzenia Holder'a:
ponieważ
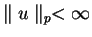 , i zbiór
, i zbiór
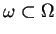 jest ograniczony w
jest ograniczony w
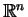 .
Uwaga. Będziemy stosować takie nierówności:
.
Uwaga. Będziemy stosować takie nierówności:
- a)
- Nierówność Holdera: Niech
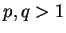 i
i
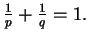 Wtedy
Wtedy
- b)
- Nierówność Young'a : Niech
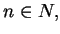
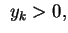
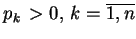 ;
;
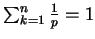 ,
to
,
to
- c)
- Nierówność Minkowskiego:
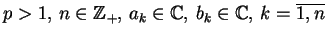 :
:



Next: Funkcje uogólnione.
Up: Podstawowe pojęcia oraz przestrzenie
Previous: Podstawowe pojęcia oraz przestrzenie
Andrzej Janus Szef
2001-12-05
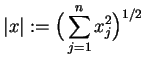
![]() (zdefiniowanych na
(zdefiniowanych na ![]() ) i mających
ciągłe pochodne łącznie do rzędu
) i mających
ciągłe pochodne łącznie do rzędu
![]() będziemy oznaczać
będziemy oznaczać
![]() . Podzbiór
funkcji, które mają pochodne do rzędu
. Podzbiór
funkcji, które mają pochodne do rzędu
![]() ciągłe na
ciągłe na
![]() , jest oznaczany jako
, jest oznaczany jako
![]() .
.
![]() . Z defenicji, nośnik
. Z defenicji, nośnik ![]()
![]() Nośnik
Nośnik ![]()
![]() jest oczywiście zbiorem domkniętym. Przypomnijmy
także, że zbiór
jest oczywiście zbiorem domkniętym. Przypomnijmy
także, że zbiór
![]() jest zwarty gdy
jest zwarty gdy ![]() jest ograniczony i domknięty w
jest ograniczony i domknięty w ![]() . Ważną klasą funkcij
są funkcje, których nośnik jest zwarty. To znaczy, że funkcja
z tej klasy jest tożsamościowo zerowa zewnątrz kuli
wystarczająco dużego promienia:
. Ważną klasą funkcij
są funkcje, których nośnik jest zwarty. To znaczy, że funkcja
z tej klasy jest tożsamościowo zerowa zewnątrz kuli
wystarczająco dużego promienia: ![]()
![]()
![]()
![]() złożony z
funkcji ze zwartymi nośnikami, oznaczamy przez
złożony z
funkcji ze zwartymi nośnikami, oznaczamy przez
![]() . Szczególnie interesujące są funkcje klasy
. Szczególnie interesujące są funkcje klasy
![]() .
.
![]() to
to
![]() w niektórym paśmie około granicy.
w niektórym paśmie około granicy.
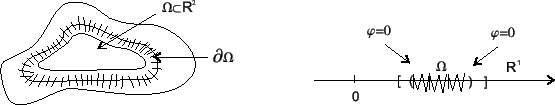

![]() jest zbiórem funkcji klasy
jest zbiórem funkcji klasy
![]() , tj.
, tj.
![]() .
.
![]() z topologią granicy indukcyjnej wszystkich
topologii (1.11) z różnymi
z topologią granicy indukcyjnej wszystkich
topologii (1.11) z różnymi
![]() i
i
![]() .
Mówimy, że ciąg
.
Mówimy, że ciąg
![]() dąży do zera gdy
dąży do zera gdy
![]() , w sensie
, w sensie
![]() jeśli spełnione dwa warunki:
jeśli spełnione dwa warunki: