Next: Transformacja Fourier'a dystrybucji. Równość
Up: Podstawowe pojęcia oraz przestrzenie
Previous: .
Pojęcie funkcji uogólnionej było wprowadzone przez S.L.Sobolewa
(1935) i L.Schwarza (1950), którzy zdefiniowali funkcję
uogolnioną jako liniowy ciągły funkcjonał nad pewną liniową
przestrzenią topologiczną tzw. ,,podstawowych'' lub
,,próbnych'' funkcji.
Jako przestrzeń funkcji podstawowych wybierają
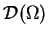 . Niech
. Niech
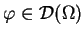 i
i
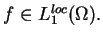 Całka Lebesgue'a
Całka Lebesgue'a
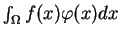 istnieje i ciągle zależy od
istnieje i ciągle zależy od
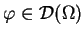 wg zbieżności w
wg zbieżności w
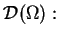 jeśli
jeśli
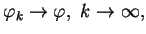 w sensie
w sensie
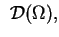 to
to
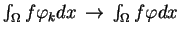 . Tak więc,
odwzorowanie
. Tak więc,
odwzorowanie
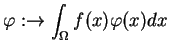 |
(1.18) |
definiuje liniowy ciagły funkcjonał na
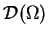 .
Oznaczamy funkcjonał (1.16) jako
.
Oznaczamy funkcjonał (1.16) jako
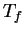 :
:
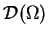
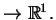 Oczywiście
Oczywiście
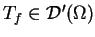 ,
sprzężonej z
,
sprzężonej z
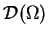 . Mamy więc
. Mamy więc
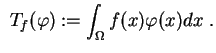 |
(1.19) |
Gdy
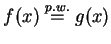 na
na
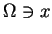 wg miary
Lebesgue'a, to oczywiście
wg miary
Lebesgue'a, to oczywiście 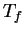
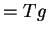 na
na
 Ma miejsce twierdzene odwrotne:
Ma miejsce twierdzene odwrotne:
Lemat 1.2 (Dubois-Reimond'a.)
Jeśli
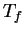
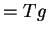
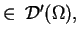
to
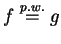
na
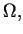
jeśli
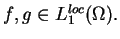
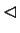 Ponieważ
Ponieważ 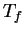
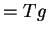 na
na
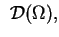 otrzymujemy że
otrzymujemy że 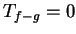 na
na
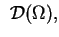 i
wystarczy teraz udowodnić że
i
wystarczy teraz udowodnić że
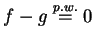 na
na 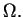 Tak więc mamy udowodnić że
Tak więc mamy udowodnić że 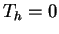 wtedy i tylko wtedy,
kiedy
wtedy i tylko wtedy,
kiedy
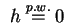 na
na
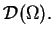 Niech
Niech
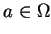 jest dowolnym punktem w
jest dowolnym punktem w 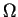 i
i
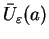 będzie domkniętą kulą całkiem
zawartą w
będzie domkniętą kulą całkiem
zawartą w 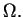 Teraz dla dowolnego
Teraz dla dowolnego
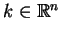 funkcja
funkcja
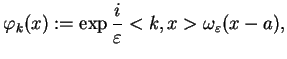 |
(1.20) |
gdzie
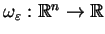 jest ,,czapeczką'', należy oczywiście do
przestrzeni
jest ,,czapeczką'', należy oczywiście do
przestrzeni
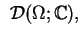 i można stosować
funkcjonał
i można stosować
funkcjonał 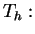
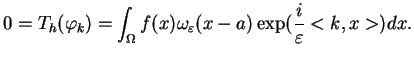 |
(1.21) |
Tak więc, wszystkie współczynniki wg układu trygonometrycznego
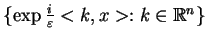 dla
funkcji
dla
funkcji
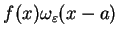 na kuli
na kuli
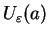 są równe zero. Stąd wnioskujemy, że ta funkcja, tj.
są równe zero. Stąd wnioskujemy, że ta funkcja, tj.
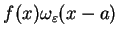 jest pw. równa zero na
jest pw. równa zero na
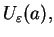 co jest równoważne temu, że
co jest równoważne temu, że 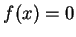 pw.
na
pw.
na
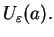 Ponieważ punkt
Ponieważ punkt
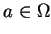 jest
dowolny, to udowodniliśmy, że
jest
dowolny, to udowodniliśmy, że
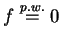 na
na
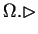
Wniosek 1.3
Każda lokalno całkowalna funkcja
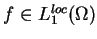
definiuje liniowy i ciągły funkcjonał na
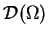
przy pomocy (
1.17), i na odwrót, funkcjonał na
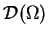
w postaci (
1.17) jednoznacznie
definiuje lokalnie całkowalną funkcję
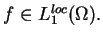
(
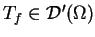
ma
nazwę regularnego).
Niech teraz
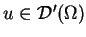 jest
dowolnym niekoniecznie regularnym funkcjonałem na
jest
dowolnym niekoniecznie regularnym funkcjonałem na
Definicja 1.4
Pochodna uogólniona
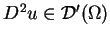
istnieje dla wszystkich
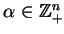
jako funkcjonał na
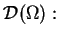
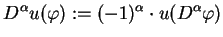 |
(1.22) |
dla każdego
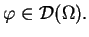
Oczywiście, gdy dla
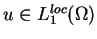 istnieje funkcja
istnieje funkcja
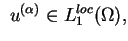 taka że
taka że
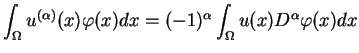 |
(1.23) |
dla wszystkich
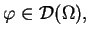 to
to
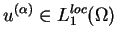 nazywa się odpowiednią uogolnioną
pochodną rzędu
nazywa się odpowiednią uogolnioną
pochodną rzędu
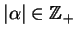 od funkcji
od funkcji
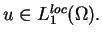 Na mocy lematu (1.2)
Dubois-Reimond'a pochodna
Na mocy lematu (1.2)
Dubois-Reimond'a pochodna
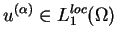 jest jedyna.
jest jedyna.
Definicja 1.5
1Wszystkie funkcjonały
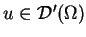
które nie są regularne nazywamy
funkcjonałami osobliwymi.
Klasycznym przykładem funkcjonału osobliwego na
 jest tzw.
jest tzw. 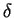 -funkcja Diraca :
-funkcja Diraca :
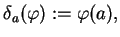 |
(1.24) |
gdzie
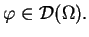 Nośnikiem
Nośnikiem 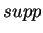
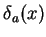 jest jeden punkt
jest jeden punkt
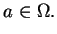
Definicja 1.6
Nośnikiem funkcjonału
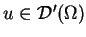
jest domknięcie zbioru punktów
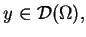
takich że
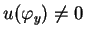
dla
wszystkich
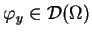
spełniających
taki warunek:
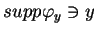
.
Zachodzą twierdzenia.
Twierdzenie 1.7 (L.Schwarz.)
Funkcja uogólniona
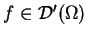
przedłuża się do funkcjonału
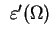
wtedy i tylko wtedy kiedy
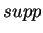
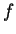
jest zwartym podzbiorem w
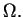
Zachodzi twierdzenie, które podamy bez dowodu.
Twierdzenie 1.8 (L.Szhwarz.)
Uogólniona funkcja z nośnikiem w jednym punkcie
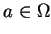
jest skończoną kombinacją liniowa
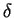
-funkcji i jej pochodnych.
Teraz wprowadźmy pojęcie rzędu funkcji uogólnionej. Dla tego
weźmy przestrzeń
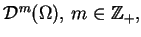 gdzie
gdzie
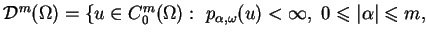
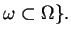
Lemat 1.9
Mają miejsce następujące gęste i ciągłe zanurzenia:
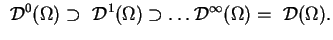 |
(1.25) |
 Dowód na zadanie do domu
Dowód na zadanie do domu .
Jeśli
.
Jeśli
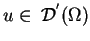 można
rozszerzyć do funkcjonału liniowego na
można
rozszerzyć do funkcjonału liniowego na
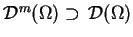 , gdzie
, gdzie 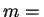 minimalną z
możliwych liczb, to mówimy, że funkcja uogólniona
minimalną z
możliwych liczb, to mówimy, że funkcja uogólniona
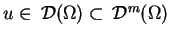 ma rząd
ma rząd
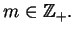
Uwaga 1.10
Liniowe ciągłe funkcjonały na
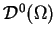
nazywają się miarami Radona i odgrywają ważną role w
teorii całkowania.
Zachodzi następne twierdzenie.
Twierdzenie 1.11 (L.Schwarz)
Każda funkcja uogólniona (tj. ,,dystrybucja'') ze zwartym
nośnikiem ma skończony rząd.
W sposób analogiczny można zdefiniować dystrybucje
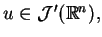 które nazywamy
funkcjami uogólnionymi umiarkowanymi. Zachodzi następne
twierdzenie.
które nazywamy
funkcjami uogólnionymi umiarkowanymi. Zachodzi następne
twierdzenie.
Twierdzenie 1.12
Jeśli
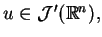
to
istnieje ciągła funkcja
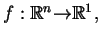
rosnąca potęgowo i taka że
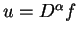
przy pewnym
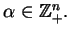



Next: Transformacja Fourier'a dystrybucji. Równość
Up: Podstawowe pojęcia oraz przestrzenie
Previous: .
Andrzej Janus Szef
2001-12-05