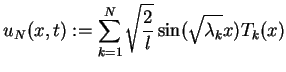Next: Problem Cauchy'ego dla trójwymiarowego
Up: Problem Cauchy'ego dla równań
Previous: Problem Gaursat'a. Istnienie i
Rozważmy na początek jednorodne równanie falowe
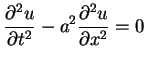 |
(8.58) |
gdzie
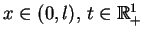 oraz
oraz
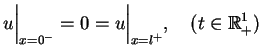 |
|
|
(8.59) |
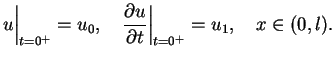 |
|
|
|
Będziemy konstruować rozwiązanie równania (8.58)
przy pomocy metody rozdzielenia zmiennych. W tym celu znajdziemy
szczególne rozwiązanie równania (8.58) w postaci
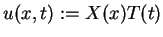 dla
dla
 i
i
 .
Podstawiając jego w (8.58) otrzymujemy:
.
Podstawiając jego w (8.58) otrzymujemy:
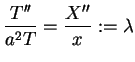 |
(8.60) |
gdzie
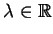 jest liczbą stałą ponieważ nie
zależy na mocy (8.60) od
jest liczbą stałą ponieważ nie
zależy na mocy (8.60) od
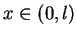 i
i
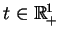 . Tak więc mamy równanie
. Tak więc mamy równanie
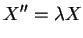 |
(8.61) |
dla którego stosujemy warunek brzegowy (8.59)
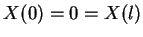 |
(8.62) |
Rozwiązując (8.61) przy warunkach (8.62)
znajdujemy że
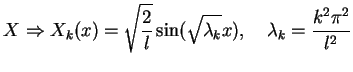 |
(8.63) |
dla wszystkich
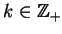 . Analogicznie dla funkcji
. Analogicznie dla funkcji
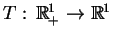 znajdujemy równanie
znajdujemy równanie
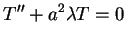 |
(8.64) |
które ma takie względem (8.63) rozwiązania:
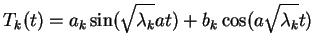 |
(8.65) |
gdzie
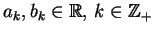 są
dowolne stałe. Oczywiście teraz, że suma
są
dowolne stałe. Oczywiście teraz, że suma
![$\displaystyle u_{N}(x,t):=\sum_{k=1}^{N}\Big[a_{k}\sin(\sqrt{\lambda_{k}}at)+b_{k}\cos(a\sqrt{\lambda_{k}}t)\Big]\sqrt{\frac{2}{l}}\sin(\sqrt{\lambda_{k}}x)$](img851.gif) |
(8.66) |
dla każdego
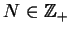 na mocy liniowości równania
(8.58) też spełnia to równanie. Problem teraz
pozostaje w dobraniu takich liczb
na mocy liniowości równania
(8.58) też spełnia to równanie. Problem teraz
pozostaje w dobraniu takich liczb
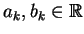 ,
,
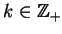 , (gdy
, (gdy
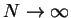 ), żeby granica
), żeby granica
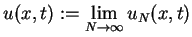 |
(8.67) |
w pewnym sensie spełniała równanie (8.58) i warunki
początkowe (8.59).
To znaczy że przy 
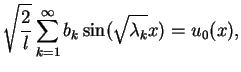 |
|
|
(8.68) |
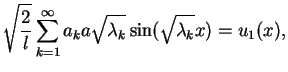 |
|
|
|
dla
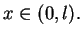 Na mocy faktu że funkcja
Na mocy faktu że funkcja
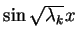 dla różnych
dla różnych
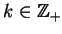 są
ortogonalne wg iloczynu skalarnego w
są
ortogonalne wg iloczynu skalarnego w
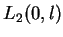 z
(8.68) otrzymujemy takie wyrażenia:
z
(8.68) otrzymujemy takie wyrażenia:
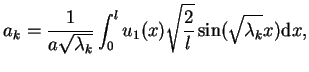 |
|
|
(8.69) |
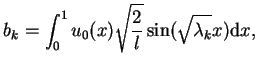 |
|
|
|
| |
|
|
|
dla wszystkich
 .
.
Jest oczywistym że rozwiązanie (8.67) jest ,,formalnym'', ponieważ
nie ustalone pojęcia zbieżności po
 . Oprócz tego
stosowaliśmy róźniczkowanie całego szeregu (8.67) po
. Oprócz tego
stosowaliśmy róźniczkowanie całego szeregu (8.67) po
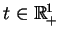 , co też nie jest uzasadnione.
, co też nie jest uzasadnione.
Niech teraz równanie (8.58) jest uogólnione do postaci
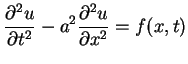 |
(8.70) |
gdzie
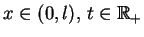 oraz
oraz
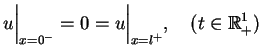 |
|
|
(8.71) |
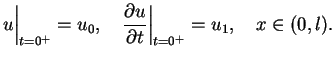 |
|
|
|
W sposób całkiem analogiczny stosując metodę rozdzielenia
zmiennych otrzymujemy, że dla
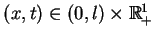
 |
(8.72) |
gdzie
dla
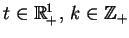
![$\displaystyle T_{k}(t)=\frac{1}{a\sqrt{\lambda_{k}}}\int_{0}^{t}f_{k}(t)\sin[a\sqrt{\lambda_{k}}(t-
\tau)] \mathrm{d}\tau$](img869.gif) |
|
|
(8.73) |
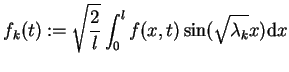 |
|
|
|
Zajmijmy się teraz uzadadnieniem tej metody Fourier'a dla
problemu (8.59) nakładając na funkcje
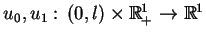 pewne
ograniczenia. Niech
pewne
ograniczenia. Niech
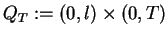 jest cylindrem w
jest cylindrem w
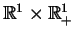 . Rozwiązanie klasyczne
powinno z definicji należeć do przestrzeni
. Rozwiązanie klasyczne
powinno z definicji należeć do przestrzeni
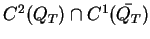 . Wtedy oczywiście
. Wtedy oczywiście
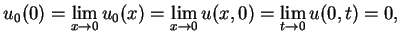 |
|
|
(8.74) |
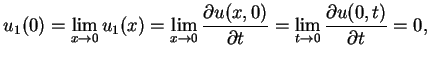 |
|
|
|
Podobne warunki sę też przy  . To znaczy, że muszą
być spełnione warunki zgodności
. To znaczy, że muszą
być spełnione warunki zgodności
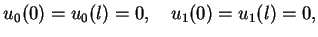 |
(8.75) |
Można teraz dla
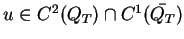 sformułować następujące twierdzenie
sformułować następujące twierdzenie
Twierdzenie 8.5
Jeżeli
![$\displaystyle u_{0}\in C^2([0,l]),\,u_{1}\in C^1([0,l]), \quad u''_{0}\in
L^2(0,l),\,u''_{1}\in L_{2}(0,l),$](img880.gif) |
(8.76) |
oraz spełnione są warunki zgodności (
8.75), to suma
(
8.67) jest rozwiązaniem klasycznym równania
(
8.58) z klasą
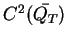
dla każdego
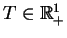
.



Next: Problem Cauchy'ego dla trójwymiarowego
Up: Problem Cauchy'ego dla równań
Previous: Problem Gaursat'a. Istnienie i
Andrzej Janus Szef
2001-12-05
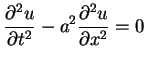
![]() . Oprócz tego
stosowaliśmy róźniczkowanie całego szeregu (8.67) po
. Oprócz tego
stosowaliśmy róźniczkowanie całego szeregu (8.67) po
![]() , co też nie jest uzasadnione.
, co też nie jest uzasadnione.