Uwaga 10.6
Hans Lewi w 1957 r. pokazał że równanie
nie posiada dla żadnej funkcji
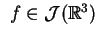
rozwiązania z klasy
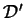
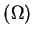
dla wszystkich
obszarów
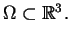
Tym nie mniej dla operatoró
w różniczkowych (
10.1) ze stałymi wspólczynnikami
posiada zawsze rozwiązanie podstawowe (Twierdzenie Malgrange'a i
Erenpreise'a) z klasy
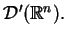
W
przypadku klasy funkcji
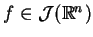
było
udowodnione takie twierdzenie.
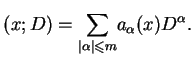
![$\displaystyle \mathcal{A}u=u^{\prime \prime }+a^{2}u\Rightarrow E(x;y)=\vartheta
(x-y) \frac{1}{a}\sin [a(x-y)].
$](img1036.gif)