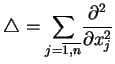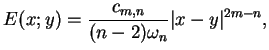Next: Podstawowe rozwiązania operatorów parabolicznych.
Up: Podstawowe rozwiązania operatorów różniczkowych.
Previous: Pojęcie rozwiązania podstawowego.
Rozważmy równania Laplace'a
Rozwiązanie podstawowe spelnia równanie
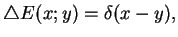 |
(10.23) |
lub stosując transformacje Fourier'a,
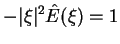 , , |
(10.24) |
tj.
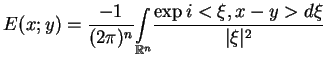 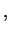 |
(10.22) |
gdzie potrzeba obliczyć całkę, co jest skoplikowanym zadaniem.
Z drugiej strony, jest prosto udowodnić że rozwiązanie
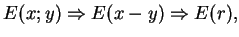 gdzie
gdzie 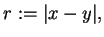 tj.
posiada symetrię centralną. Wtedy, można łatwo otrzymać że
tj.
posiada symetrię centralną. Wtedy, można łatwo otrzymać że
Niech teraz 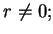 wtedy z (10.23) otrzymujemy że
wtedy z (10.23) otrzymujemy że
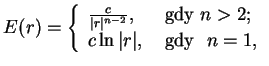 |
(10.27) |
gdzie
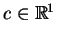 jest liczbą stałą.Żeby wyznaczyć
tę liczbę
jest liczbą stałą.Żeby wyznaczyć
tę liczbę
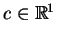 , zastosujmy do lewej strony
(10.21)
działanie na element
, zastosujmy do lewej strony
(10.21)
działanie na element
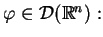
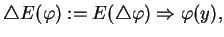 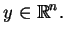 |
(10.28) |
Ponieważ
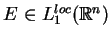 jest lokalnie
całkowalną (!), to oczywiście dla
jest lokalnie
całkowalną (!), to oczywiście dla
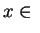 supp
supp
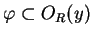
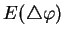 |
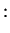 |
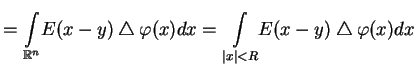 |
(10.29) |
| |
|
 |
(10.30) |
| |
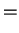 |
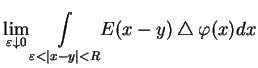 |
(10.31) |
| |
|
 |
(10.32) |
| |
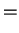 |
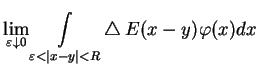 |
(10.33) |
| |
|
 |
(10.34) |
| |
|
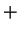 ![$\displaystyle \underset{\left\{ \left[ \vert x-y\vert=\varepsilon \right] \cup
...
...}}-\varphi \frac{\partial
E(x-y)}{\partial
\overrightarrow{n}}\right] dS \notag$](img1073.gif) |
(10.35) |
| |
|
 |
(10.36) |
| |
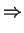 |
![$\displaystyle \underset{\vert x-y\vert=\varepsilon }{\int }\left[
E(x-y)\frac{\...
...}-\varphi \frac{\partial
E(x-y)}{\partial \overrightarrow{n}}\right] dS, \notag$](img1075.gif) |
(10.37) |
| |
|
 |
(10.38) |
gdzie skorzystaliśmy z warunków
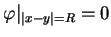 ,
,
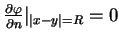 dla
dla
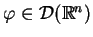 . Pozostała
całka w (10.27) może być obliczona w następujący
sposób: przy
. Pozostała
całka w (10.27) może być obliczona w następujący
sposób: przy
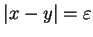
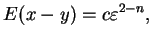 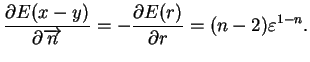 |
(10.39) |
Stosując teraz (10.28) do (10.27), na
podstawie twierdzenia o wartości średniej dla całek,
otrzymujemy:
gdzie
 jest powierzchnią sfery
jest powierzchnią sfery  o promieniu 1.
Tak więc, na mocy dowolności parametra
o promieniu 1.
Tak więc, na mocy dowolności parametra
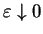
dla wszystkich
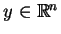 i
i
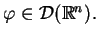 Jako wniosek z (10.30)
otrzymujemy, że stała
Jako wniosek z (10.30)
otrzymujemy, że stała
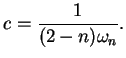 |
(10.44) |
Tak więc, rezultat dla
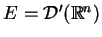 dla
dla 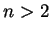 jest taki :
jest taki :
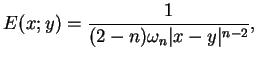 |
(10.45) |
gdzie
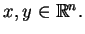 W sposób analogiczny znajdujemy że dla
W sposób analogiczny znajdujemy że dla 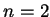
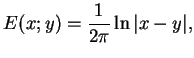 |
(10.46) |
gdzie
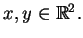 Stosując taki sam schemat wyprowadzenia, znajdujemy, że rozwią
zanie podstawowe dla równania
Stosując taki sam schemat wyprowadzenia, znajdujemy, że rozwią
zanie podstawowe dla równania
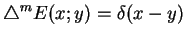 |
(10.47) |
ma postać:
gdzie
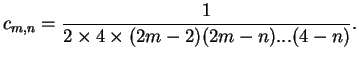 |
(10.48) |
Jeśli
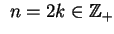 i
i 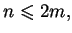 to
to
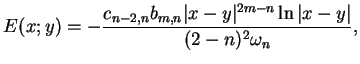 |
(10.49) |
gdzie
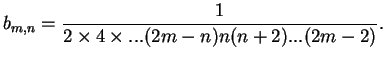 |
(10.50) |
Dla równania
rozwiązanie podstawowe ma postać:
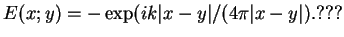 |
(10.52) |



Next: Podstawowe rozwiązania operatorów parabolicznych.
Up: Podstawowe rozwiązania operatorów różniczkowych.
Previous: Pojęcie rozwiązania podstawowego.
Andrzej Janus Szef
2001-12-05