


Next: Potencjały dla równań hipo-eliptycznych.
Up: Potencjały dla równań fizyki
Previous: Potencjały dla równań fizyki
Niech
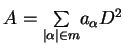 jest
wyrażeniem różniczkowym i
jest
wyrażeniem różniczkowym i
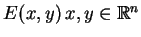 ,
jest jego rozwiązaniem podstawowym.
,
jest jego rozwiązaniem podstawowym.
Definicja 11.1
Potencjałami dla tego wyrażenia różniczkowego
nazywamy sploty
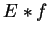
z różnymi funkcjami uogólnionymi
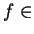
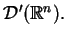
W zależności od struktury funkji uogólnionej
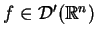 otrzymujemy różne potencjały fizyki
matematycznej, mające fizyczny sens.
Niech
otrzymujemy różne potencjały fizyki
matematycznej, mające fizyczny sens.
Niech
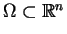 jest obszarem ograniczonym w
jest obszarem ograniczonym w
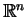 i
i
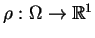 jest
lokalnie całkowalną funkcją w
jest
lokalnie całkowalną funkcją w
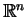 , tj.
, tj.
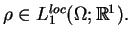 Zdefiniujmy funkcję
Zdefiniujmy funkcję
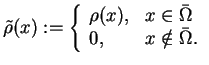 |
(11.1) |
jest oczywistym teraz, że
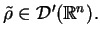 Rozważmy teraz splot
Rozważmy teraz splot
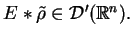
Definicja 11.2
Splot
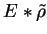
, gdzie
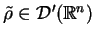
jest zdefiniowana przez
(
11.1), nazywamy potencjałem objętości
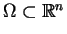
(obszaru
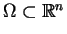
)
dla operatora
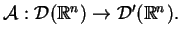
Niech teraz
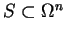 jest wystarczająco gładką,
ograniczoną obu-stronną powierzchnią w
jest wystarczająco gładką,
ograniczoną obu-stronną powierzchnią w
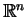 , a
, a
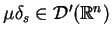 jest
warstwą prostą z gęstością
jest
warstwą prostą z gęstością
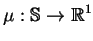 i z nośnikiem supp
i z nośnikiem supp
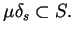 Oczywiście, że
Oczywiście, że
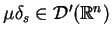 jest dystrybucją i działanie jej na
jest dystrybucją i działanie jej na
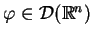 oznaczone jako
oznaczone jako
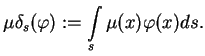 |
(11.2) |
Definicja 11.4
Splot
![$ E\ast \left[ -\frac{\partial }{
\partial \vec{n}}(\nu \delta _{s})\right] $](img1295.gif)
, gdzie
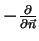
(
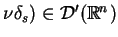
jest warstwą podwójną, nazywamy potencjałem warstwy
podwójnej z gęstością
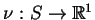
.
Potencjały są ważnymi środkami dla konstruowania rozwiązań
różnych problemów brzegowych dla równań liniowych z
operatorem
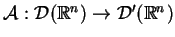 .
.
Ponieważ splot funkcji uogólnionych nie zawsze istnieje, to jest ważnym
wyjaśnienie tego problemu dla szczególnych klas operatorów
różniczkowych
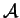 .
.



Next: Potencjały dla równań hipo-eliptycznych.
Up: Potencjały dla równań fizyki
Previous: Potencjały dla równań fizyki
Andrzej Janus Szef
2001-12-05
![]() .
.