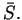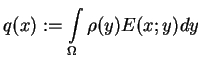Potencjały dla równań
hipo-eliptycznych.

Dla hipo-eliptycznych operatorów $\mathcal{A}:\mathcal{D}\rightarrow \mathcal{D}$ rozwiązanie podstawowe ma osobliwość tylko przy $x=y\in \Omega$ i jest funkcją gładką. Wtedy oczywiście, mamy:

$$q(x):=\int\limits_{\Omega }\rho (y)E(x;y)dy$$ (11.3)

jest potencjałem objętości $\Omega \subset \mathbb{R}^{n}$;

$$u(x):=\int\limits_{\partial \Omega =S}E(x;y)\mu (y)dS_{y}$$ (11.4)

jest potencjałem warstwy prostej;

$$v(x):=\int\limits_{\partial \Omega =S}\nu (y)\frac{\partial E(x,y)}{\partial n_{y}}dS_{y}$$ (11.4)

jest potencjałem warstwy podwójnej. Ponieważ $E(x,y)$ przy $x=y$ ma osobliwość, to całki (11.3-11.3) są oczywiście osobliwe, które charakteryzuje takie twierdzenie.

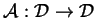
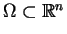
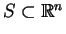
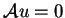
Twierdzenie 11.5   Niech operator $\mathcal{A}:\mathcal{D}\rightarrow \mathcal{D}$ jest hipoeliptyczny, a gęstości potencjałów (11.3)-(11.4) są kawałkami-ciągłe i ograniczone w $\Omega \subset \mathbb{R}^{n}$ i $S\subset \mathbb{R}^{n}$ odpowiednio. 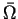Wtedy potencjały (11.3)-(11.5) są nieskonczenie razy ró żniczkowalne i spełniają równanie jednorodne $\mathcal{A}u=0$ w każdym obszarze, nie mającym wspólnych punktów z $\bar{\Omega}$ i $\bar{S}.$

$\lhd$ Dowód jest wprost na mocy tego że $\mathcal{A}E(x;y)=0$ dla wszystkich
$x\notin (\bar{\Omega} \cup \bar{S})$. $\rhd$