Next: Problemy brzegowe dla równań
Up: Potencjały dla równań fizyki
Previous: Potencjały dla równań hipo-eliptycznych.
Niech 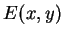 ,
,
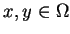 , jest rozwiązaniem
podstawowym dla równania Laplace'a. Wtedy potencjał objętości
, jest rozwiązaniem
podstawowym dla równania Laplace'a. Wtedy potencjał objętości
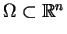
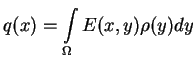 , , 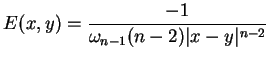 |
(11.5) |
dla wszystkich
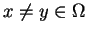 . Będziemy dalej stosować
taką definicję całki osobliwej.
. Będziemy dalej stosować
taką definicję całki osobliwej.
Definicja 11.6
Niech zadana jest całka
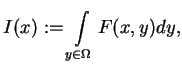 |
(11.6) |
gdzie
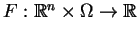
jest funkcją ciągłą przy
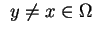
i ma
osobliwość przy
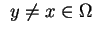
. Wtedy całka
(
11.6) nazywa się jednostajnie zbieżną w punkcie
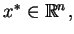
jeśli dla każdego
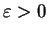
istnieje takie
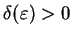
, że
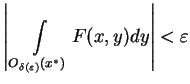 |
(11.7) |
dla każdego otoczenia
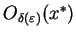
o
promieniu
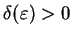
i wszystkich
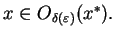
Zgodnie z tą definicją,
całka
(
11.7) może być przedstawiona w postaci
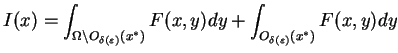 |
(11.8) |
gdzie pierwsza całka w (
11.8) jako funkcja od
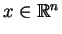
jest ciągła w
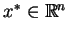
, a druga jest niesko
ńczenie mała dla
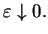
Zachodzi takie twierdzenie, które podamy bez dowodu.
Twierdzenie 11.7
Całka (
11.6)
jest zbieżną jednostajnie w każdym punkcie
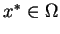
, gdy istnieje takie otoczenie
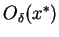
punktu
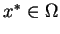
i stałe
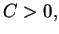
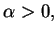
że
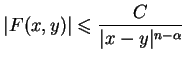 |
(11.9) |
dla wszystkich
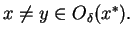
Na mocy twierdzenia 11.7 stwierdzamy prawdziość
takich twierdzeń.
Twierdzenie 11.8
Jeżeli gęstość potencjału obj
ętości (
11.5) jest kawalkami ciągła i ograniczona w
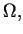
to potencjał (
11.5) jest określony i ciągle różniczkowalny w
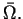
Twierdzenie 11.9
Jeżeli gęstość potencjału
(
11.4) dla równania Laplace'a jest ograniczona i kawałkami cią
gła na
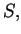
to potencjał warstwy prostej (
11.4) jest funkcją klasy
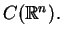
Zapiszmy teraz potencjał warstwy podwójnej dla równania Laplace'a:
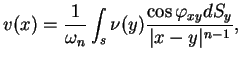 |
(11.10) |
gdzie
 i
i
 jest kątem
między kierunkiem od
jest kątem
między kierunkiem od
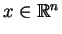 do
do 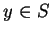 i wektorem
normalnym
i wektorem
normalnym
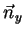 do
do 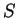 w punkcie
w punkcie 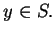 Rozważmy najpierw tzw. całkę Gauss'a
Rozważmy najpierw tzw. całkę Gauss'a
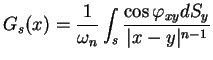 |
(11.11) |
gdzie
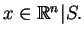 Ponieważ wyrażenie
Ponieważ wyrażenie
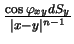 jest kątem bryłowym, pod którym
jest widoczny element
jest kątem bryłowym, pod którym
jest widoczny element 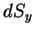 powierzchni
powierzchni 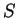 z punktu
z punktu
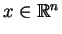 , to będziemy uważać, że ten kąt jest dodatni, gdy
, to będziemy uważać, że ten kąt jest dodatni, gdy
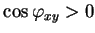 i ujemnym gdy
i ujemnym gdy
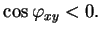 Wtedy, oczywiście, całka Gauss'a (11.11) równa się
kątowi bryłowemu pod którym jest widoczna cała powierzhnia
Wtedy, oczywiście, całka Gauss'a (11.11) równa się
kątowi bryłowemu pod którym jest widoczna cała powierzhnia 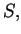 podzielonemu na pełny kąt bry"lowy
podzielonemu na pełny kąt bry"lowy
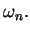
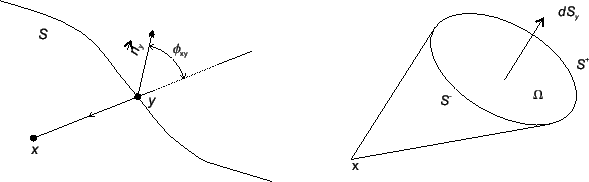
Rys. 8
|
Jak widac z Rys.2 , zachodzi taka własność dla całki
(11.11):
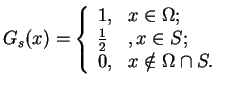 |
(11.12) |
Własność (11.12) zachodzi dla wszystkich powierzchni
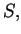 które mają nazwę Lapunowskie.
które mają nazwę Lapunowskie.
Uwaga 11.11
Można udowodnić (S.Michlin), że
wystarczą tylko warunki i) oraz ii), a warunek iii) będzie ich
skutkiem.
Teraz można sformułować bez dowodu nastepujące twierdzenie.
Twierdzenie 11.12
Jeżeli gęstość potencjału
warstwy podwójnej
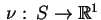
jest ograniczona i kawałkami ciągła, a
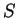
jest powierzchnią
lapunowa, to potencjał warstwy podwójnej (
11.10)
będzie funkcją ciągłą od
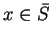
.
Ponieważ twierdzenie (11.11) mówi tylko o ciąglości
potencjału warstwy podwójnej (11.10) na 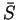 ,
to powstaje pytanie o jego ciągłość na zewnątrz
,
to powstaje pytanie o jego ciągłość na zewnątrz 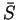 przy przejściu przez powierzchnię
przy przejściu przez powierzchnię
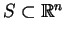 .
Zachodzi takie twierdzenie.
.
Zachodzi takie twierdzenie.
Twierdzenie 11.13
Niech
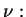
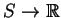
jest
ograniczona, kawalkami ciągła na
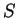
oraz ciągła w punkcie
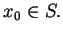
Wtedy potencjał warstwy podwójnej (
11.10)
istnieje dla
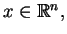
istnieją wartości graniczne
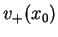
oraz
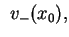
równe
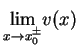
. Oprócz tego
prawdziwe są takie własności:
Analogiczna własność zachodzi dla pochodnych potencjału
warstwy prostej (11.4) dla równania Laplace'a w punkcie
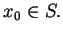 Mianowicie
Mianowicie
gdzie, z definicji
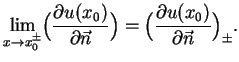 |
(11.17) |
Rozważmy teraz równanie Laplace'a w postaci
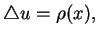 |
(11.18) |
gdzie
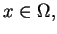
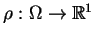 jest funkcją ograniczoną, kawałkami ciągłą oraz są zadane
warunki brzegowe
jest funkcją ograniczoną, kawałkami ciągłą oraz są zadane
warunki brzegowe
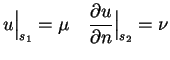 |
(11.19) |
gdzie
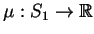 i
i
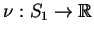 są też ograniczone i kawa"lkami ciągłe na
są też ograniczone i kawa"lkami ciągłe na
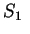 i
i 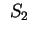 , odpowiednio. Wtedy zachodzi takie
twierdzenie.
, odpowiednio. Wtedy zachodzi takie
twierdzenie.
Zastosujemy teraz pojęcie potencjału dla równań typu
parabolicznego. Rozważmy takie równanie paraboliczne:
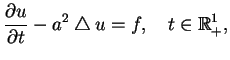 |
(11.21) |
którego rozwiązanie
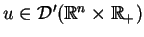 spełnia warunek brzegowy na
powierzchni Lapunowa
spełnia warunek brzegowy na
powierzchni Lapunowa
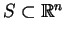 :
:
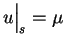 , , 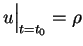 |
(11.22) |
i gdzie
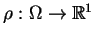 ,
,
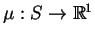 są to funkcje ograniczone i
kawałkami ciągłe, a
są to funkcje ograniczone i
kawałkami ciągłe, a
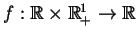 jest lokalnie
całkowalną. Wtedy zachodzi takie twierdzenie.
jest lokalnie
całkowalną. Wtedy zachodzi takie twierdzenie.
 Dowód twierdzenia jest wprost, wykorzystując własności
Dowód twierdzenia jest wprost, wykorzystując własności
 .
. Rozpisując wyrażenie (11.21) w postaci jawnej przy
Rozpisując wyrażenie (11.21) w postaci jawnej przy
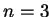 znajdujemy, że
znajdujemy, że
dla wszystkich
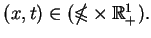
Rozważmy na koniec potencjały dla równań typu hiperbolicznego
na przykład wyrażenie
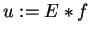 , , 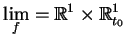 , , |
(11.27) |
gdzie
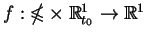 jest lokalnie
całkowalną funkcją, spełnia równanie
jest lokalnie
całkowalną funkcją, spełnia równanie
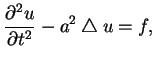 |
(11.28) |
jeśli
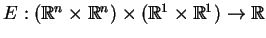 jest
jego rozwiązaniem podstawowym. Założmy także, że rozwiązanie
równania (11.24) spełnia takie warunki
jest
jego rozwiązaniem podstawowym. Założmy także, że rozwiązanie
równania (11.24) spełnia takie warunki
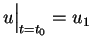 , , 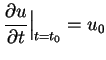 |
(11.29) |
przy dowolnym
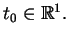 Wtedy rozwiązanie
(11.24) będzie mieć postać
Wtedy rozwiązanie
(11.24) będzie mieć postać
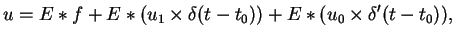 |
(11.30) |
lub w postaci jawnej przy 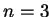 i
i
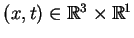
Dla przypadku 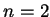 otrzymujemy w sposób analogiczny:
otrzymujemy w sposób analogiczny:
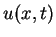 |
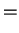 |
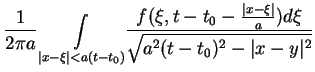 |
(11.34) |
| |
|
 |
(11.35) |
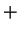 |
|
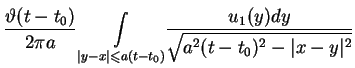 |
(11.36) |
| |
|
 |
(11.37) |
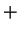 |
|
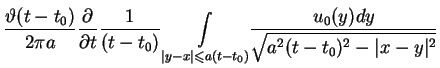 |
(11.38) |
| |
|
 |
(11.39) |
Dla przypadku  wyrażenie (11.26) przyjmuje taką
postać dla
wyrażenie (11.26) przyjmuje taką
postać dla
 :
:
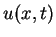 |
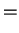 |
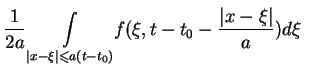 |
(11.40) |
| |
|
 |
(11.41) |
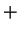 |
|
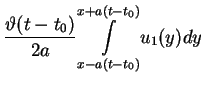 |
(11.42) |
| |
|
 |
(11.43) |
 |
|
![$\displaystyle \frac{\vartheta
(t-t_{0})}{2}[u_{0}(x+a(t-t_{0}))+u_{0}(x-a(t-t_{0}))]. \notag$](img1417.gif) |
(11.44) |
| |
|
 |
(11.45) |
Uwaga 11.17
Rozważmy problem brzegowy dla hipoeliptycznego
operatora
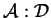
gdzie
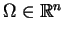
jest to obszar w
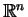
i
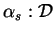
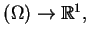
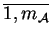
, są to liniowe
funkcjonały na
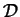
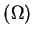
i
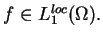
Niech teraz funkcja
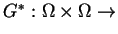
spełnia równanie
sprzężone do (
11.31):
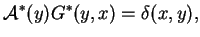 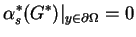 |
(11.47) |
z jednorodnymi warunkami brzegowymi. Wtedy na mocy tożsamości
Green'a zachodzi takie wyrażenie dla rozwiązania
(
11.31):
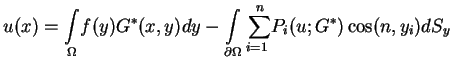 |
(11.48) |
gdzie
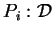
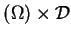
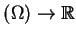
,
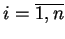
, są to wyrażenia
różniczkowe względem
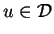
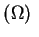
nie wyższego rzędu niż
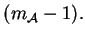
Ponieważ drugi
człon wyrażenia (
11.33) w rzeczywistości nie zawiera
w sobie niewiadomych funkcji
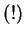
, a różne pochodne od
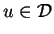
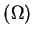
są wyznaczone przy pomocy warunków
brzegowych (
11.31). Tak więc, wyrażenie
(
11.33) daje dokładne rozwiązanie równania
(
11.31), gdy wiadoma jest jego sprzężona funkcja
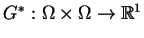
, która nosi nazwę funkcji Green'a. To znaczy,
że funkcja Green'a
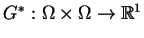
dla problemu (
11.31)
jest szczególnym rozwiązaniem podstawowym problemu sprzężonego
(
11.32). Metoda odzyskania rozwiązania problemu
(
11.31) ma odpowiednią nazwę metody funkcji Green'a.



Next: Problemy brzegowe dla równań
Up: Potencjały dla równań fizyki
Previous: Potencjały dla równań hipo-eliptycznych.
Andrzej Janus Szef
2001-12-05
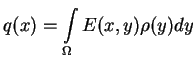 ,
,