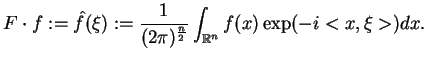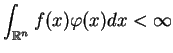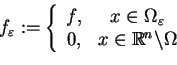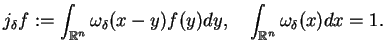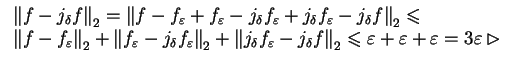Next: Przestrzenie Sobolewa.
Up: Podstawowe pojęcia oraz przestrzenie
Previous: Funkcje uogólnione.
Nech
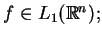 wówczas mamy definicję jej
transformacji Fourier'a
wówczas mamy definicję jej
transformacji Fourier'a
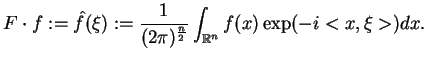 |
(1.26) |
Odwrotna transformacja Fourier'a ma postać:
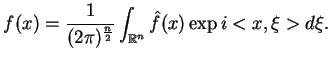 |
(1.27) |
Gdy element
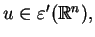 całka
(1.24) nie jest zdefiniowana, przez co rozważmy
następującą tożsamość Parsewale'a dla
całka
(1.24) nie jest zdefiniowana, przez co rozważmy
następującą tożsamość Parsewale'a dla
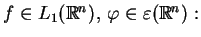
Tożsamość (1.26) bierzemy za definicję transformacji Fourier'a
elementu
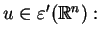
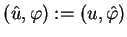 |
(1.31) |
dla wszystkich
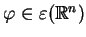 gdy
gdy
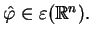 Jeżeli
Jeżeli
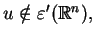 a na
przykład
a na
przykład
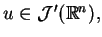 to definicja (1.27) jest prawdziwa, ponieważ dla
to definicja (1.27) jest prawdziwa, ponieważ dla
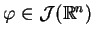 również
również
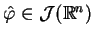 .
Na mocy tego że
.
Na mocy tego że
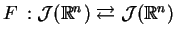 i jest odwzorowaniem ciągłym,
otrzymujemy wniosek.
i jest odwzorowaniem ciągłym,
otrzymujemy wniosek.
Niech teraz
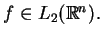 Oczywiście że na mocy
twierdzenia Schwartza-Cauchy'ego całka
istnieje i ciągle zależy od
Oczywiście że na mocy
twierdzenia Schwartza-Cauchy'ego całka
istnieje i ciągle zależy od
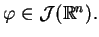 Stosując wzór (1.27)
Stosując wzór (1.27)
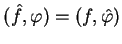 |
(1.33) |
dla
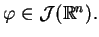 Z (1.29)
wnioskujemy że transformacja Fouriera
Z (1.29)
wnioskujemy że transformacja Fouriera 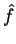 elementu
elementu
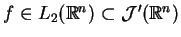 jako dystrybucji należy też do
jako dystrybucji należy też do
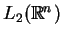 , tj.
, tj.
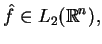
oraz
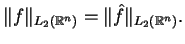
Ten sam wniosek otrzymujemy bazując na następującym lemacie:
 Dowód. Niech
Dowód. Niech
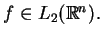 Wtedy
istnieje zbiór
Wtedy
istnieje zbiór
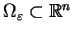 dla
dla
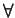
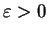 taki że
taki że
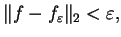
gdzie
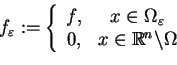
Oczywiście
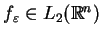 i
i
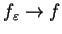 gdy
gdy
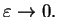 Weźmy teraz funkcję ,,czapeczkę''
Weźmy teraz funkcję ,,czapeczkę''
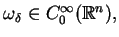 i utworzymy funkcję
która istnieje dla wszystkich
i utworzymy funkcję
która istnieje dla wszystkich
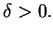 Mamy też że
Mamy też że
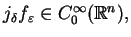 dla
każdego
dla
każdego
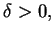 oraz na mocy równości Parsewala
oraz na mocy równości Parsewala
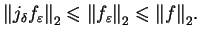 Stąd mamy:
Stąd mamy:
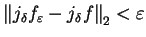 dla zadanych
dla zadanych
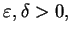 tj.
WNIOSKI SCHWARZA.
tj.
WNIOSKI SCHWARZA.
- a)
- Dystrybucja
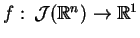 będzie umiarkowanie rosnąca wtedy i tylko wtedy,
kiedy jej aproksymacja
będzie umiarkowanie rosnąca wtedy i tylko wtedy,
kiedy jej aproksymacja
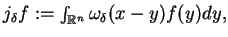 jest funkcją umiarkowanego wzrostu przy
każdym
jest funkcją umiarkowanego wzrostu przy
każdym
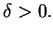
- b)
- Dystrybucja
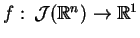 będzie umiarkowanie rosnąca wtedy i tylko wtedy,
kiedy jest ona (uogólnioną) pochodną pewnej ciągłej funkcji
umiarkowanego wzrostu.
będzie umiarkowanie rosnąca wtedy i tylko wtedy,
kiedy jest ona (uogólnioną) pochodną pewnej ciągłej funkcji
umiarkowanego wzrostu.



Next: Przestrzenie Sobolewa.
Up: Podstawowe pojęcia oraz przestrzenie
Previous: Funkcje uogólnione.
Andrzej Janus Szef
2001-12-05