


Next: Wzory Green'a.
Up: Problemy brzegowe dla równań
Previous: Problemy brzegowe dla równań
Załóżmy, że obszar
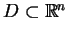 jest ograniczony, a jego granica
jest ograniczony, a jego granica
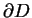 jest kawałkami ciągła. Rozważmy następujący problem
brzegowy dla równania eliptycznego typu:
jest kawałkami ciągła. Rozważmy następujący problem
brzegowy dla równania eliptycznego typu:
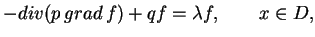 |
(12.1) |
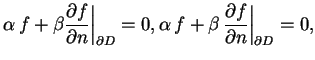 |
(12.2) |
gdzie
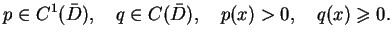 |
(12.3) |
dla
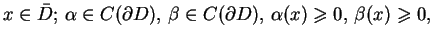
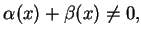
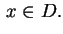 Niech
Niech
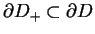 jest podzbiór
jest podzbiór
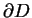 gdzie
gdzie
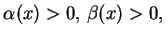
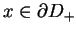 jednostajnie. Problem (12.1) - (12.3) polega w
znalezieniu funkcji
jednostajnie. Problem (12.1) - (12.3) polega w
znalezieniu funkcji 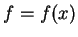 klasy
klasy
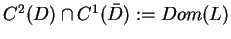 Wyrażenie (12.1) definiuje
operator
Wyrażenie (12.1) definiuje
operator
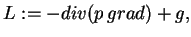 |
(12.4) |
dla którego (12.1) jest problemem dla wartości
własnych:
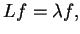 gdzie
gdzie
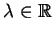 , oraz
połóżmy że
, oraz
połóżmy że
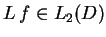 , co równoważne oczywiście
, co równoważne oczywiście
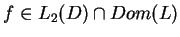 .
.
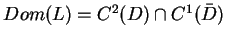 jest dziedziną operatora
jest dziedziną operatora 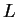 .
.
Andrzej Janus Szef
2001-12-05
![]() jest ograniczony, a jego granica
jest ograniczony, a jego granica
![]() jest kawałkami ciągła. Rozważmy następujący problem
brzegowy dla równania eliptycznego typu:
jest kawałkami ciągła. Rozważmy następujący problem
brzegowy dla równania eliptycznego typu: