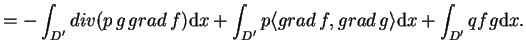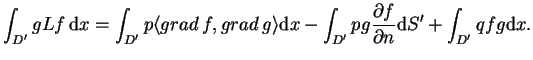Next: Własności operatora
Up: Problemy brzegowe dla równań
Previous: Problem na wartości własne
Jeśli
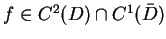 i
i
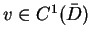 , to jest prawdziwy pierwszy wzór Green'a:
, to jest prawdziwy pierwszy wzór Green'a:
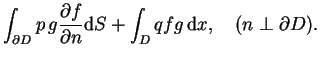 |
(12.5) |
Niech
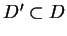 jest dowolny obszar wewnątrz
jest dowolny obszar wewnątrz 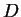 z brzegiem
z brzegiem
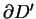 też kawałkami gładkim. Wtedy oczywiście z
warunku
też kawałkami gładkim. Wtedy oczywiście z
warunku
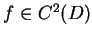 wynika, że
wynika, że
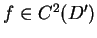 , tak więc
całka
Stosując teraz wyrażenie Gauss'a-Ostrogradskiego, otrzymujemy:
Biorąc teraz granice, gdy
, tak więc
całka
Stosując teraz wyrażenie Gauss'a-Ostrogradskiego, otrzymujemy:
Biorąc teraz granice, gdy
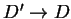 i korzystając z
tego, że
i korzystając z
tego, że
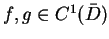 , znajdujemy że granica
, znajdujemy że granica
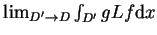 istnieje i zachodzi
równość (12.5). Niech teraz
istnieje i zachodzi
równość (12.5). Niech teraz
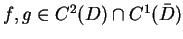 wtedy prawdziwy jest drugi wzór Green'a:
wtedy prawdziwy jest drugi wzór Green'a:
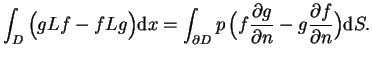 |
(12.6) |
Dowód jest na mocy wzoru (12.5) przy
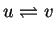 i dalszego ich odejmowania.
i dalszego ich odejmowania.
Andrzej Janus Szef
2001-12-05
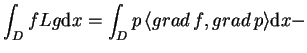
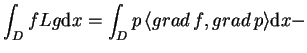
![$\displaystyle \int_{D'}gLf \, \mathrm{d}x= \int_{D'}g \big[-div (p \, grad\, f)+qf
\big] \mathrm{d}x=
$](img1467.gif)