


Next: Problem spektralny dla operatora
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Zagadnienie odwrotne problemu spektralnego
Niech iperator liniowy
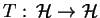 ma dziedzinę
ma dziedzinę
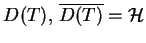 , gdzie
, gdzie
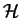 jest przestrzenią Hilberta.
jest przestrzenią Hilberta.
Definicja 14.1
Operator
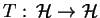
nazywa się
symetrycznym gdy dla dowolnych
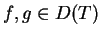
zachodzi:
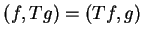 |
(14.1) |
Zdefiniujemy teraz operator sprzężont do operatora
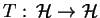 . Niech
. Niech
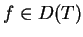 i
i
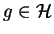 jest taki element, że iloczyn skalarny
jest taki element, że iloczyn skalarny
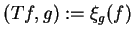 |
(14.2) |
definiuje dla wszystkich
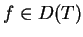 ograniczony funkcjonał liniowy
ograniczony funkcjonał liniowy
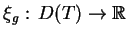 |
(14.3) |
to znaczy
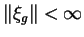 . Wtedy ten funkcjonał
(14.2) może być przedłużony na całość
. Wtedy ten funkcjonał
(14.2) może być przedłużony na całość
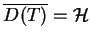 , co daje możliwość zastosowania
Tw. Riesz'a do funkcjonału (14.2). Mianowicie, istnieje
wtedy takie element
, co daje możliwość zastosowania
Tw. Riesz'a do funkcjonału (14.2). Mianowicie, istnieje
wtedy takie element
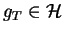 , który spełnia
równość
, który spełnia
równość
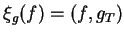 |
(14.4) |
dla wszystkich
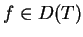 . Z drugiej strony na mocy
(14.4) można zdefiniować dla takich
. Z drugiej strony na mocy
(14.4) można zdefiniować dla takich
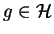 odwzorowanie
odwzorowanie
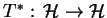 , że
, że
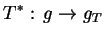 |
(14.5) |
które jest oczywiście liniowym. Ten zbiór elementów
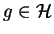 dla których zachodzi (14.5) nazwiemy
dziedziną
dla których zachodzi (14.5) nazwiemy
dziedziną 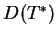 , a sam operator (14.5) sprzężonym
do operatora
, a sam operator (14.5) sprzężonym
do operatora
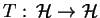 . Na
ogół dziedzina
. Na
ogół dziedzina 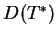 może być domknięta w
może być domknięta w
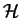 .
.
Lemat 14.2
Niech
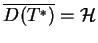
; wtedy operator
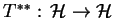
istnieje i zachodzi
własność:
Dowód jest wprost jako ćwiczenie.
Niech teraz operator
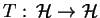 nazywa się samosprzężonym, gdy
nazywa się samosprzężonym, gdy 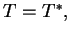
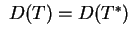 .
.
Ponieważ na ogół
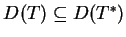 dla operatora
symetrycznego ma sens pojęcie roszerzenia samosprzężonego operatora symetrycznego.
dla operatora
symetrycznego ma sens pojęcie roszerzenia samosprzężonego operatora symetrycznego.
Definicja 14.3
Niech
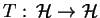
oraz
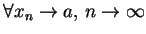
i
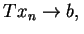
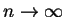
w
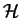
, gdzie
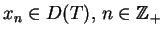
. Jeśli wówczas zachodzi
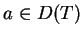
i
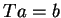
to
operator
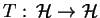
nazywa się
domnkniętym.
Jest oczywistym że operator
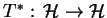 jest zawsze domniętym. Jeśli operator
jest zawsze domniętym. Jeśli operator
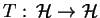 jest symetrycznym, jest możliwość
odzyskania jego rozszerzeń samosprzężonych. Takich rozszerzń
może być dużo, gdyż istnieje dla symetrzycznego operatora
jest symetrycznym, jest możliwość
odzyskania jego rozszerzeń samosprzężonych. Takich rozszerzń
może być dużo, gdyż istnieje dla symetrzycznego operatora
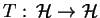 tylko jedno rozszerzenie
symetryczne, ono nazywa się rozszerzeniem właściwym.
tylko jedno rozszerzenie
symetryczne, ono nazywa się rozszerzeniem właściwym.
Zbadamy kilka operatorów symetrycznych w przestrzeni Hilberta
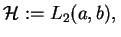
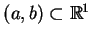 .
.
Niech
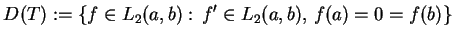 |
(14.6) |
gdzie dla każdego
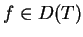
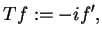 |
(14.7) |
i funkcja
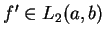 jest rozumiana jako pochodna w
sensie teorii dystrybucji dla każedgo
jest rozumiana jako pochodna w
sensie teorii dystrybucji dla każedgo
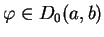
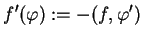 |
(14.8) |
Jest oczywistym, że operator (14.7) jest symetrycznym:
dla
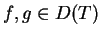
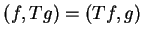 |
(14.9) |
Znajdujemy teraz sprzężony operator
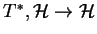 do (14.7). Niech
do (14.7). Niech
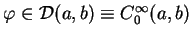 i obliczamy
wyrażenie (14.2) przy
i obliczamy
wyrażenie (14.2) przy
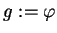 :
:
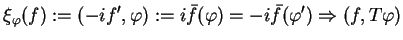 |
(14.10) |
dla wszystkich
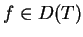 . Jest oczywistym, że (14.10)
jest ograniczonym funkcjinałem dla każdego
. Jest oczywistym, że (14.10)
jest ograniczonym funkcjinałem dla każdego
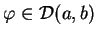 , tj. istnieje operator sprzężony
, tj. istnieje operator sprzężony
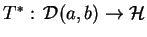 , taki
że
, taki
że
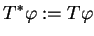 |
(14.11) |
dla wszystkich
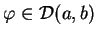 . Tak więc, na
podstawie (14.11) i wzięcia domknięcia przestrzeni
. Tak więc, na
podstawie (14.11) i wzięcia domknięcia przestrzeni
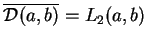 , wnioskujemy że
, wnioskujemy że
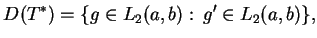 |
(14.12) |
gdzie, dzięki (14.11)
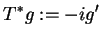 |
(14.13) |
dla wszystkich
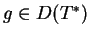 .
.
Ponieważ
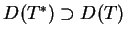 , wnioskujemy także że operator różniczkowania (14.7) nie jest samosprzężony w
, wnioskujemy także że operator różniczkowania (14.7) nie jest samosprzężony w
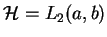 .
.
Zadania ćwiczeń:
- a)
-
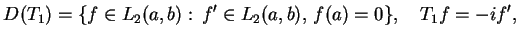 |
(14.14) |
wtedy
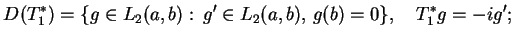 |
(14.15) |
- b)
-
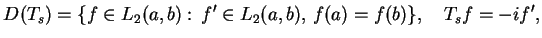 |
(14.16) |
wtedy
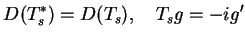 |
(14.17) |
dla
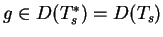 , tj. operator
, tj. operator
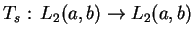 jest samosprzężonym na
jest samosprzężonym na
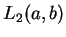 .
.
Rozważmy teraz operator Schturm'a-Liouville'a z jednym punktem
osobliwym przy
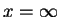 :
:
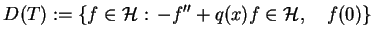 |
(14.18) |
gdzie
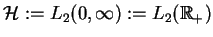 , oraz
dla
, oraz
dla
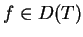
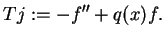 |
(14.19) |
Funkcja
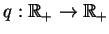 jest
wybrana tutaj ciągłą i nieujemną, tj.
jest
wybrana tutaj ciągłą i nieujemną, tj.
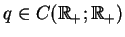 .
.
Naszym zadaniem będzie odzyskanie operatora sprzężonego do
(14.19). Dość prosto sprawdzić że operator (14.19) jest symetrycznym, tj.
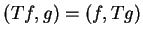 |
(14.20) |
dla wszystkich
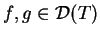 .
.
Zbadamy własności operatora (14.19) na przestrzeni
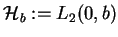 . Ponieważ
. Ponieważ
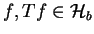 dla każdego
dla każdego
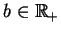 , oraz
, oraz
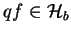 ,
to
,
to
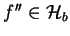 także dla każdego
także dla każdego
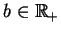 .
Z tego wynika, że funkcje
.
Z tego wynika, że funkcje 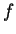 oraz
oraz 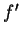 są ciągłe na półosi
są ciągłe na półosi
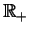 , tj.
, tj.
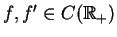 . Warunek brzegowy
. Warunek brzegowy 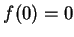 jest oczywiście ważny, ponieważ
jest oczywiście ważny, ponieważ
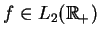 .
.
POnieważ
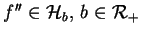 ,
całkowaniem przez części znajdujemy:
,
całkowaniem przez części znajdujemy:
Ostatnia całka w (14.21) może dążyć przy
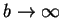 do liczby dodatniej lub nieskończoności. W drugim
przypadku, oczywiście
do liczby dodatniej lub nieskończoności. W drugim
przypadku, oczywiście
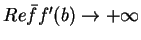 , co powoduje
do
, co powoduje
do
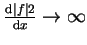 , co przeczy
cakowalności z kwadratem funkcji
, co przeczy
cakowalności z kwadratem funkcji
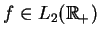 .
Tak więc, z (14.21) otrzymujemy, że
.
Tak więc, z (14.21) otrzymujemy, że
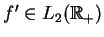 oraz
oraz
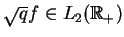 .
.
Przejdziemy teraz do znalezienia
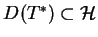 dla symetrycznego operatora
dla symetrycznego operatora
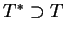 . Jak wyżej, niech
. Jak wyżej, niech
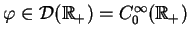 i rozważmy następne wyrażenie dla
i rozważmy następne wyrażenie dla
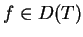 :
:
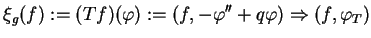 |
(14.22) |
gdzie oczywiście funkcjonał (14.22) jest ograniczony na
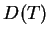 . Wtedy można zdefiniować operator sprzężony
. Wtedy można zdefiniować operator sprzężony
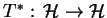 jako
jako
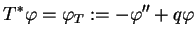 |
(14.23) |
dla wszystkich
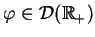 . Niech
teraz
. Niech
teraz
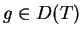 tj. na mocy (14.23)
tj. na mocy (14.23)
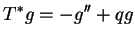 |
(14.24) |
Z (14.24) analogicznie do (14.21) zachodzi że
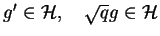 . Teraz dla
każdego
. Teraz dla
każdego
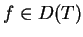 oraz
oraz
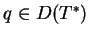 znajdujemy że
znajdujemy że
![$\displaystyle (f, -\varphi'' + q \varphi) = \lim_{b \to \infty}\Big[ -\bar{f'}g
\big\vert _{0}^{b} + \int_{0}^{b}(\bar{f'}g'+ q \bar{f}g) \mathrm{d}x \Big]$](img1770.gif) |
(14.25) |
Całka w (14.25) jest skończona, ponieważ
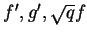 oraz
oraz
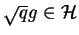 . Wobec granicy
. Wobec granicy
![$ \lim_{b \to \infty}\big[ \bar{f'(0)}g(0)-\bar{f'(b)}g(b)
\big]=0$](img1773.gif) można przewidzieć że granica
można przewidzieć że granica
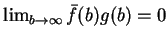 , ponieważ całka
, ponieważ całka
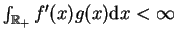 . Całkując
(14.25) przez części, otrzymujemy teraz wyrażenie
. Całkując
(14.25) przez części, otrzymujemy teraz wyrażenie
![$\displaystyle (-f'' +qf,g)=\bar{f'}(0)g(0)+ \lim_{b \to \infty}\Big[ \bar{f}g'
\big\vert _{0}^{b}+ \int_{0}^{b}\bar{f}(-g''+qg)\mathrm{d}x \Big]$](img1776.gif) |
(14.26) |
Na mocy (14.24) całka (14.26) istnieje, tj.
istnieje granica
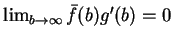 ,
ponieważ
,
ponieważ
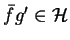 . Tak więc, z warunku
. Tak więc, z warunku
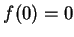 otrzymujemy z (14.26) że
otrzymujemy z (14.26) że
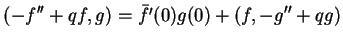 |
(14.27) |
Ponieważ
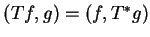 na mocy definicji operatora
sprzężonego
na mocy definicji operatora
sprzężonego
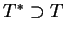 , z (14.27)
otrzymujemy że
, z (14.27)
otrzymujemy że
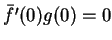 , tj.
, tj. 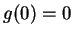 . Stąd widzimy
że
. Stąd widzimy
że
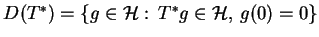 , tj,
, tj,
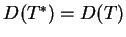 z czego wnioskujemy, że operator
z czego wnioskujemy, że operator
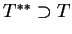 , tj, jest samosprzężony.
, tj, jest samosprzężony.
Wniosek W przypadku gdy
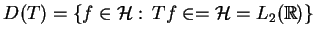 |
(14.28) |
operator liniowy
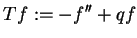 |
(14.29) |
na całej osi
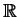 będzi też samosprzężony bez
żadnego warunku brzegowego, tj.
będzi też samosprzężony bez
żadnego warunku brzegowego, tj. 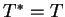 .
.
Dowód jako ćwiczenie.
Jak juz mówiliśmy wcześniej, są operatory domknięte na
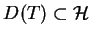 . W przypadku gdy operator nie jest domknięty
on może mieć domknięte rozszerzenie
. W przypadku gdy operator nie jest domknięty
on może mieć domknięte rozszerzenie
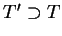 z dziedziną
z dziedziną
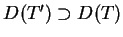 . W przypadku gdy takie domknięte rozszerzenie ma
. W przypadku gdy takie domknięte rozszerzenie ma
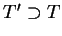 ma najmniejszą dziedzinę
ma najmniejszą dziedzinę 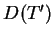 z możliwych, to operator
z możliwych, to operator
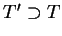 nazywamy domknięciem operatora
nazywamy domknięciem operatora
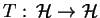 .
.
Z samej definicji zachodzi, że operator
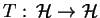 ma domknięcie wtedy i tylko wtedy kiedy zachodzi
taka własność: jeśli dla każdego ciągu
ma domknięcie wtedy i tylko wtedy kiedy zachodzi
taka własność: jeśli dla każdego ciągu
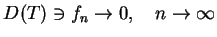 istnieje granica
istnieje granica
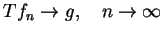 to
to 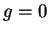 . Tak więc
. Tak więc
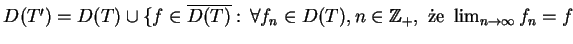 oraz
oraz
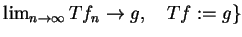 .
.



Next: Problem spektralny dla operatora
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Zagadnienie odwrotne problemu spektralnego
Andrzej Janus Szef
2001-12-05
![]() nazywa się samosprzężonym, gdy
nazywa się samosprzężonym, gdy ![]()
![]() .
.
![]() dla operatora
symetrycznego ma sens pojęcie roszerzenia samosprzężonego operatora symetrycznego.
dla operatora
symetrycznego ma sens pojęcie roszerzenia samosprzężonego operatora symetrycznego.
![]() jest zawsze domniętym. Jeśli operator
jest zawsze domniętym. Jeśli operator
![]() jest symetrycznym, jest możliwość
odzyskania jego rozszerzeń samosprzężonych. Takich rozszerzń
może być dużo, gdyż istnieje dla symetrzycznego operatora
jest symetrycznym, jest możliwość
odzyskania jego rozszerzeń samosprzężonych. Takich rozszerzń
może być dużo, gdyż istnieje dla symetrzycznego operatora
![]() tylko jedno rozszerzenie
symetryczne, ono nazywa się rozszerzeniem właściwym.
tylko jedno rozszerzenie
symetryczne, ono nazywa się rozszerzeniem właściwym.
![]()
![]() .
.
![]() , wnioskujemy także że operator różniczkowania (14.7) nie jest samosprzężony w
, wnioskujemy także że operator różniczkowania (14.7) nie jest samosprzężony w
![]() .
.
![]() . Ponieważ
. Ponieważ
![]() dla każdego
dla każdego
![]() , oraz
, oraz
![]() ,
to
,
to
![]() także dla każdego
także dla każdego
![]() .
Z tego wynika, że funkcje
.
Z tego wynika, że funkcje ![]() oraz
oraz ![]() są ciągłe na półosi
są ciągłe na półosi
![]() , tj.
, tj.
![]() . Warunek brzegowy
. Warunek brzegowy ![]() jest oczywiście ważny, ponieważ
jest oczywiście ważny, ponieważ
![]() .
.
![]() ,
całkowaniem przez części znajdujemy:
,
całkowaniem przez części znajdujemy:
![]() dla symetrycznego operatora
dla symetrycznego operatora
![]() . Jak wyżej, niech
. Jak wyżej, niech
![]() i rozważmy następne wyrażenie dla
i rozważmy następne wyrażenie dla
![]() :
:
![]() . W przypadku gdy operator nie jest domknięty
on może mieć domknięte rozszerzenie
. W przypadku gdy operator nie jest domknięty
on może mieć domknięte rozszerzenie
![]() z dziedziną
z dziedziną
![]() . W przypadku gdy takie domknięte rozszerzenie ma
. W przypadku gdy takie domknięte rozszerzenie ma
![]() ma najmniejszą dziedzinę
ma najmniejszą dziedzinę ![]() z możliwych, to operator
z możliwych, to operator
![]() nazywamy domknięciem operatora
nazywamy domknięciem operatora
![]() .
.
![]() ma domknięcie wtedy i tylko wtedy kiedy zachodzi
taka własność: jeśli dla każdego ciągu
ma domknięcie wtedy i tylko wtedy kiedy zachodzi
taka własność: jeśli dla każdego ciągu
![]() istnieje granica
istnieje granica
![]() to
to ![]() . Tak więc
. Tak więc
![]() oraz
oraz
![]() .
.