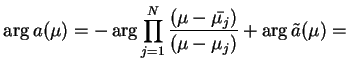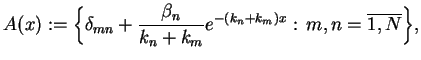Next: About this document ...
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Schemat Gefllanda-Levitana- -Marczenki.
Żeby wykorzystać jądra (14.78) dla rozwiązania
równania całkowego (14.78), musimy mieć więcej
informacji o funkcji
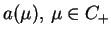 , spełniającej
równość (14.75) dla
, spełniającej
równość (14.75) dla
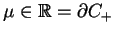 , które można także przepisać w postaci
, które można także przepisać w postaci
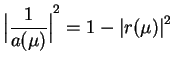 |
(14.82) |
ponieważ
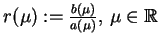 .
.
Teraz przyjmijmy do uwagi że funkcja
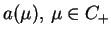 , jest analityczna w
, jest analityczna w 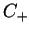 i ma tam skończoną ilość zer. Rozważmy wyrażenie
i ma tam skończoną ilość zer. Rozważmy wyrażenie
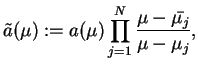 |
(14.83) |
gdzie
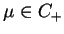 . Oczywiście, że funkcja
. Oczywiście, że funkcja
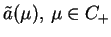 jest analityczna na
jest analityczna na 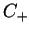 i nie ma tam żednego
zera; oprócz tego dla
i nie ma tam żednego
zera; oprócz tego dla
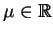
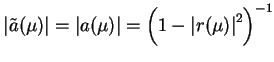 |
(14.84) |
Rozważmy teraz funkcję
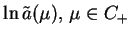 ,
która jest analityczna na
,
która jest analityczna na 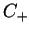 i spełnia warunki twierdzenia
Jordana. To znaczy, że sprawiedliwa reprezentacja
i spełnia warunki twierdzenia
Jordana. To znaczy, że sprawiedliwa reprezentacja
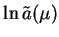 w takiej postaci:
w takiej postaci:
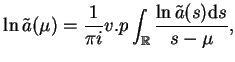 |
(14.85) |
gdzie
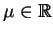 . Ponieważ dla
. Ponieważ dla
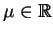
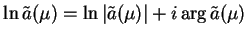 |
(14.86) |
stosując (14.85) znajdujemy, że
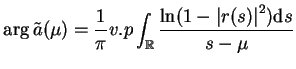 |
(14.87) |
dla wszystkich
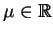 . Tak więc, na mocy wyrażenia
(14.87) i reprezentacji (14.83), znajdujemy
że
. Tak więc, na mocy wyrażenia
(14.87) i reprezentacji (14.83), znajdujemy
że
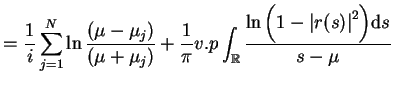 |
(14.88) |
Rozważmy teraz przypadek, gdy parametr ,,rozpraszania''
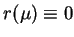 dla wszystkich
dla wszystkich
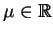 . Wtedy
oczywiście jądro
. Wtedy
oczywiście jądro
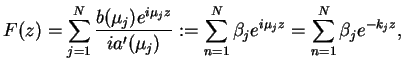 |
(14.89) |
gdzie
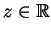 , oraz położyliśmy
, oraz położyliśmy
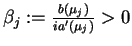 ,
,
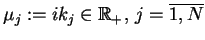 . Wtedy równanie
(14.78) ma rozwiązania w postaci rozdzielonej:
. Wtedy równanie
(14.78) ma rozwiązania w postaci rozdzielonej:
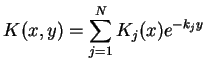 |
(14.90) |
gdzie dla
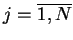
![$\displaystyle K_{j}(x)= \det\Big[\frac{A^{(j)}(x)}{A(x)}\Big]$](img1987.gif) |
(14.91) |
a macierz 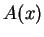 i
i
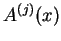 są równe
są równe
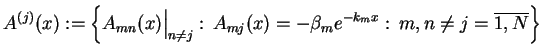 |
(14.92) |
Podstawiając (14.92) w (14.90) przy
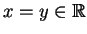 , znajdujemy, że
, znajdujemy, że
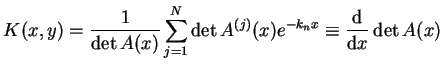 |
(14.93) |
Tak więc na podstawie wzoru (14.81) z (14.93)
otrzymujemy że
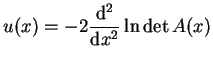 |
(14.94) |
dla
 . W przypadku
. W przypadku  od razu odzyskujemy
takie wyrażenie
od razu odzyskujemy
takie wyrażenie
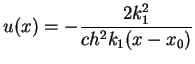 |
(14.95) |
gdzie my położyliśmy
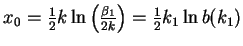 .
Jako wniosek z wyrażenia (14.95) otrzymujemy, że
operator Sturm'a-Liouville'a
.
Jako wniosek z wyrażenia (14.95) otrzymujemy, że
operator Sturm'a-Liouville'a
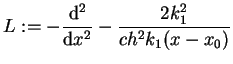 |
(14.96) |
w przestrzeni
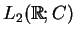 posiada tylko jedną wartość
własną
posiada tylko jedną wartość
własną
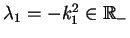 .
LITERATURA.
1. Marcinkowska H. Wstęp do teorii równań
różniczkowych cząstkowych. Warszawa, PWN, tom 43, 1986.
2. Władimirow W.S. Równania fizyki matematycznej.
Moskwa, 1981.
3. Władimirow W.S.(red.) Zbiór zadań z teorii równania fizyki matematycznej,
Warszawa, 1979.
4. Gonczarenko W.M. Podstawy teorii równań
różniczkowych
.
LITERATURA.
1. Marcinkowska H. Wstęp do teorii równań
różniczkowych cząstkowych. Warszawa, PWN, tom 43, 1986.
2. Władimirow W.S. Równania fizyki matematycznej.
Moskwa, 1981.
3. Władimirow W.S.(red.) Zbiór zadań z teorii równania fizyki matematycznej,
Warszawa, 1979.
4. Gonczarenko W.M. Podstawy teorii równań
różniczkowych
cząstkowych. Kijów, Wyższa szkoła, 1985.
5. Mizochata S. Teoria równań o pochodnych
cząstkowych. Springer, NY. 1970 (in English).



Next: About this document ...
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Schemat Gefllanda-Levitana- -Marczenki.
Andrzej Janus Szef
2001-12-05
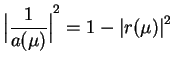
![]() , jest analityczna w
, jest analityczna w ![]() i ma tam skończoną ilość zer. Rozważmy wyrażenie
i ma tam skończoną ilość zer. Rozważmy wyrażenie