


Next: Zastosowania
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Zagadnienie odwrotne analizy spektralnej.
Zauważmy teraz że wyrażenie (14.59) może być
przepisane w uwikłanej postaci jako
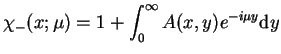 |
(14.73) |
gdzie
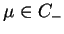 i
i
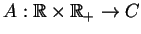 jest pewne jądro transformacji Fourier'a dla
analitycznej w
jest pewne jądro transformacji Fourier'a dla
analitycznej w 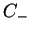 funkcji
funkcji
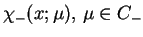 . Ponieważ
. Ponieważ
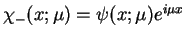 ,
,
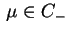 , z (14.73) otrzymujemy, że
, z (14.73) otrzymujemy, że
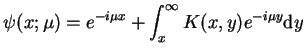 |
(14.74) |
gdzie oczywiście
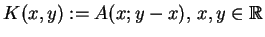 .
Wykorzystuj"ac teraz reprezentację (14.74) w wyrażeniu
(14.44) pomnożonemu przez
.
Wykorzystuj"ac teraz reprezentację (14.74) w wyrażeniu
(14.44) pomnożonemu przez
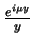 i
zcałkowaniu po wszystkich
i
zcałkowaniu po wszystkich
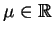 , znajdujemy:
, znajdujemy:
![$\displaystyle =\frac{1}{2 \pi i} \int_{\mathbb{R}}\mathrm{d}\mu e^{i \mu
y}\Big[\psi(x;\mu)- e^{-i \mu x} + r(\mu) \bar{\psi}(x;\mu)\Big]$](img1957.gif) |
(14.75) |
Caka po lewej stronie (14.75) może być wyliczona przy
pomocy reszt Cauchy'ego i wzorów (14.49):
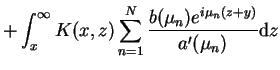 |
(14.76) |
gdzie
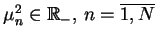 jak
wyżej są wartościami własnymi operatora (14.30).
Odpowiednio lewa strona (14.75) po podstawieniu
(14.74) sprowadza się do takiego wyrażenia:
jak
wyżej są wartościami własnymi operatora (14.30).
Odpowiednio lewa strona (14.75) po podstawieniu
(14.74) sprowadza się do takiego wyrażenia:
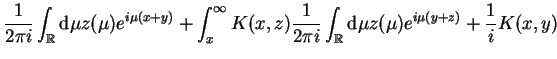 |
(14.77) |
Przyrównując teraz (14.76) i (14.77)
otrzymujemy takie równanie całkowe:
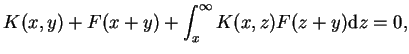 |
(14.78) |
gdzie jądro
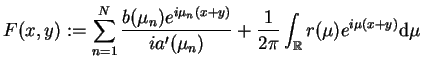 |
(14.79) |
zależy tylko od danych spektralnych ![$ S[r(L)]$](img1964.gif) .
.
Przypominając wyrażenia (14.60) i (14.74) znajdujemy że przy
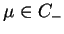 ,
,
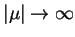
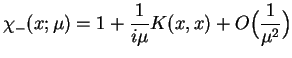 |
(14.80) |
oraz
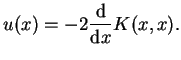 |
(14.81) |
Tak więc, rozwiązując liniowe równanie całkowe
(14.78) przy zadanym a priori jądrze
(14.79) względem jądra
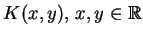 , przy pomocy wzoru (14.81) znajdujemy
dokładne wyrażenie dla potencjału
, przy pomocy wzoru (14.81) znajdujemy
dokładne wyrażenie dla potencjału
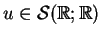 w operatorze Sturm'a-Liouville'a
(14.30) na osi
w operatorze Sturm'a-Liouville'a
(14.30) na osi
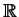 . Ostatnie zdanie oznacza
dokładnie fakt rozwiązania przez nas tutaj odwrotnego
zagadnienia problemu spektralnego dla operatora (14.30).
. Ostatnie zdanie oznacza
dokładnie fakt rozwiązania przez nas tutaj odwrotnego
zagadnienia problemu spektralnego dla operatora (14.30).



Next: Zastosowania
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Zagadnienie odwrotne analizy spektralnej.
Andrzej Janus Szef
2001-12-05
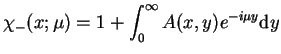
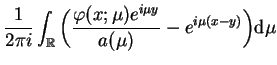
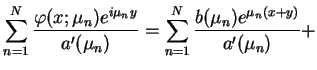
![]() ,
,
![]()