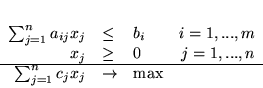Przykład 3.3 (c.d.)
Zgodnie z naszym zwyczajem, będziemy maksymalizować, a nie minimalizować,
pewną funkcję celu. Problem
|
(3.20) |
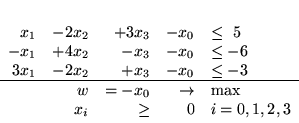 |
przyjmie po wprowadzeniu zmiennych bazowych
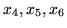
postać
|
(3.21) |
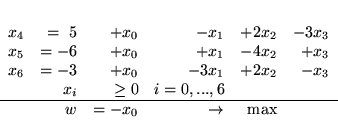 |
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nie jest słownikiem dopuszczalnym, bowiem rozwiązaniem bazowym jest
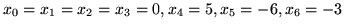
, więc
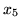
i
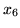
przyjmują
wartości ujemne. Ten defekt zniknie po wprowadzeniu
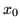
jako zmiennej
bazowej w miejsce
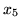
, inaczej mówiąc przyjmujemy
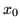
jako zmienną
wchodzącą,
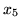
jako zmienną wychodzącą. Nowym słownikiem będzie
|
(3.22) |
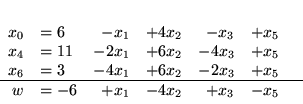 |
Teraz już (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) jest słownikiem dopuszczalnym (rozwiązanie
bazowe jest rozwiązaniem dopuszczalnym:
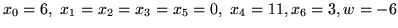
).
Zauważmy, że także w ogólnym przypadku, zawsze będzie
możliwy taki wybór zmiennej bazowej wychodzącej, żeby
pierwsza iteracja dała słownik dopuszczalny.
Wystarczy w tym celu tak wybrać 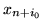 żeby
żeby 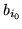 było najmniejsze spośród
było najmniejsze spośród 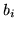 ,
, 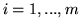 .
.
Nową zmienną bazową wchodzącą może być
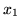
lub
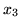
(we wzorze na
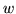
w słowniku (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) współczynniki przy tych
zmiennych są dodatnie i równe
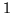
, przy pozostałych zmiennych
współczynniki są ujemne). Mamy teraz:
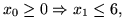
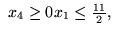
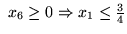
.
Wobec tego, zmienną wychodzącą jest
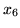
. Wyliczamy więc
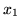
z trzeciego z równań (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
i obliczamy nowe wzory na
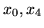
oraz
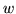
. Po elementarnych
rachunkach otrzymamy nowy słownik
|
(3.23) |
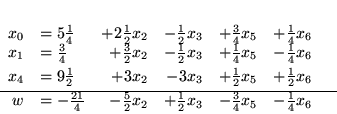 |
Zmienną wchodzącą jest teraz
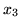
a wychodzącą
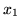
.
Wyliczamy więc
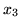
z drugiego ze
wzorów słownika (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
), a następnie wstawiamy do pozostałych eliminując
w ten sposób
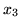
.
Nowym słownikiem jest następujący układ równań:
|
(3.24) |
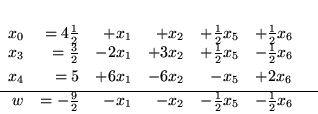 |
Wartością maksymalną jaką może przyjąć
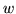
w problemie
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) jest
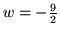
, a więc liczba ujemna, nie zero.
Oznacza to, że problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) jest sprzeczny.