




Next: Od czego zacząć?
Up: Opis metody simpleks
Previous: Tabele simpleksowe
Spis rzeczy
Indeks
Do tej pory zapoznając się z metodą simpleks skrupulatnie omijaliśmy wszelkie rafy na które można natrafić.
W szczególności przykłady były dobrane tak, by
- - po pierwsze:
- wiadomo było od czego trzeba zacząć
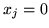 dla
dla 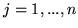 było rozwiązaniem
dopuszczalnym,
było rozwiązaniem
dopuszczalnym,
- - po drugie:
- raz rozpoczęty algorytm działał bez zacięć, to znaczy: na żadnym etapie jego funkcjonowania
nie mieliśmy wątpliwości co będzie trzeba zrobić w następnym kroku i następny krok był zawsze wykonalny,
- - po trzecie:
- po trzech (co najwyżej!) zmianach zmiennych bazowych otrzymywaliśmy optymalne rozwiązanie.
Czy tak musi być zawsze? Okazuje się, że nie. Rozważmy przykład następujący.
Tym razem 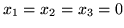 nie jest rozwiązaniem dopuszczalnym problemu, nie spełnia drugiej ani
trzeciej nierówności w PPL (
nie jest rozwiązaniem dopuszczalnym problemu, nie spełnia drugiej ani
trzeciej nierówności w PPL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Co więcej, wcale nie jest oczywistym, że takie rozwiązanie w ogóle istnieje.
). Co więcej, wcale nie jest oczywistym, że takie rozwiązanie w ogóle istnieje.
Subsections