Przykład 3.6
Niech będzie dany problem PL
|
(3.32) |
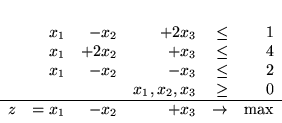 |
Kolejnymi słownikami dla tego problemu będą:
|
(3.33) |
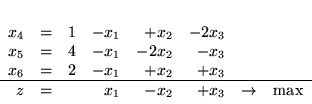 |
|
(3.34) |
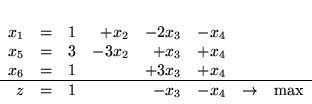 |
Zauważmy, że wartość maksymalna
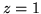
jest przyjęta dla
więcej niż jednego wektora
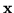
. Rzeczywiście, we wzorze na
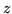
słownika (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
), a więc ostatniego słownika w metodzie simpleks
dla naszego problemu, nie występuje zmienna bazowa
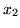
.
Jeżeli we wzorze na 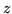 w ostatnim słowniku występują
wszystkie zmienne niebazowe, to rozwiązanie jest jedyne: zmienne
niebazowe muszą w rozwiązaniu maksymalizującym
w ostatnim słowniku występują
wszystkie zmienne niebazowe, to rozwiązanie jest jedyne: zmienne
niebazowe muszą w rozwiązaniu maksymalizującym 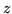 być
równe zeru, zaś zmienne bazowe wyznaczone są jednoznacznie
przez odpowiednie równania słownika
być
równe zeru, zaś zmienne bazowe wyznaczone są jednoznacznie
przez odpowiednie równania słownika. W naszym przykładzie,
aby
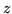
było równe
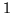
musi zachodzić
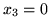
oraz
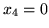
, natomiast
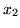
niekoniecznie jest równe zero. Na przykład dla
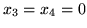
,
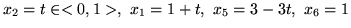
wartość
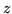
jest także równa wartości
maksymalnej
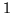
. Dla problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) oznacza to, jak łatwo stwierdzić,
że zbiorem wszystkich rozwiązań jest
zbiór punktów odcinka
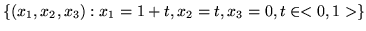
.