




Next: Ile jest rozwiązań optymalnych?
Up: Szczegóły metody
Previous: Czy simpleks może się
Spis rzeczy
Indeks
Zacznijmy od przykładu.
Przykład 3.4
Rozważmy słownik
|
(3.25) |
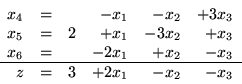 |
Rozwiązaniem bazowym tego słownika jest
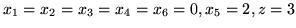
.
Zmienną wchodzącą będzie
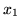
, zaś zmienną wychodzącą może być
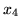
lub
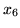
. Wybierzmy na przykład
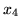
. Nowym słownikiem będzie:
|
(3.26) |
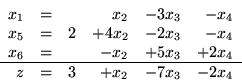 |
Zauważmy więc, że na naszej operacji zamiany słownika nic nie zyskaliśmy
w tym sensie, że wartość
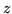
nie wzrosła.
Sytuacja w której zastąpienie jednej ze zmiennych bazowych zmienną niebazową
według podanych przez nas reguł nie spowoduje zwiększenia wartości
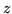 w rozwiązaniu bazowym może zajść tylko wtedy, gdy wartość jednej ze
zmiennych w rozwiązaniu bazowym wynosi zero. W naszym przykładzie takimi zmiennymi
były
w rozwiązaniu bazowym może zajść tylko wtedy, gdy wartość jednej ze
zmiennych w rozwiązaniu bazowym wynosi zero. W naszym przykładzie takimi zmiennymi
były 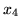 i
i 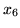 dla słownika (
dla słownika (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i
) i 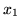 i
i 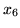 dla słownika (
dla słownika (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Definicja 3.3
Mówimy, że rozwiązanie bazowe słownika jest zdegenerowane jeżeli co
najmniej jedna zmienna bazowa w tym rozwiązaniu przyjmuje wartość zero.
Odpowiedni słownik także nazywamy zdegenerowanym.
Przykład 3.4 (cd)
Czytelnik zechce sprawdzić, że następnym (po (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)) słownikiem
będzie
a więc simpleks doprowadził do rozwiązania optymalnego PPl (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
),
rozwiązaniem
optymalnym jest
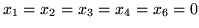
,
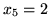
,
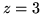
.
Ponieważ przy przejściu ze słownika (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) do (
) do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) rozwiązanie
nie polepszyło się (wartość
) rozwiązanie
nie polepszyło się (wartość 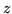 w tych słownikach jest taka sama)
powstaje pytanie, czy może zaistnieć sytuacja w której po kilku zmianach
słownika algorytm wróci do słownika który był już rozważany?
w tych słownikach jest taka sama)
powstaje pytanie, czy może zaistnieć sytuacja w której po kilku zmianach
słownika algorytm wróci do słownika który był już rozważany?
Odpowiedź na to pytanie brzmi tak! Jest jasne, że jeśli konsekwentnie według
jakiejś reguły wybieramy zmienne wchodzące i wychodzące i na jeden i ten sam
słownik wpadamy dwa razy, wtedy
te same słowniki będą sie pojawiały cyklicznie (będziemy wtedy też mówić,
że algorytm zapętla się.
Zauważmy od razu, że taka sytuacja może się pojawić tylko wtedy gdy pojawi się
słownik zdegenerowany - jeśli nie, to w każdej iteracji rozwiązanie bazowe jest
inne, różni się od wszystkich poprzednich wartością 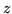 chociażby.
chociażby.
W przykładzie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) oba słowniki (
oba słowniki (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są zdegenerowane.
Czytelnik zechce sprawdzić, że przykład Chvátala [4] zaproponowany
poniżej jako ćwiczenie
) są zdegenerowane.
Czytelnik zechce sprawdzić, że przykład Chvátala [4] zaproponowany
poniżej jako ćwiczenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) jest problemem PL w którym po kilku odpowiednio
przeprowadzonych iteracjach wracamy do wyjściowego słownika 3.1.
jest problemem PL w którym po kilku odpowiednio
przeprowadzonych iteracjach wracamy do wyjściowego słownika 3.1.
Z twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika w szczególności, że każde rozwiązanie bazowe
jest rozwiązaniem każdego innego słownika (nie tylko tego którego jest
rozwiązaniem bazowym). Stąd zaś,
że wszystkich możliwych rozwiązań bazowych dla PPL jest
tyle na ile sposobów można wybrać
wynika w szczególności, że każde rozwiązanie bazowe
jest rozwiązaniem każdego innego słownika (nie tylko tego którego jest
rozwiązaniem bazowym). Stąd zaś,
że wszystkich możliwych rozwiązań bazowych dla PPL jest
tyle na ile sposobów można wybrać 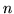 elementów (zmiennych bazowych)
spośród
elementów (zmiennych bazowych)
spośród 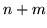 elementów (tyle jest wszystkich zmiennych), a więc
elementów (tyle jest wszystkich zmiennych), a więc
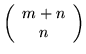 .
Tak więc słowników dla danego PPL jest skończona liczba
.
Tak więc słowników dla danego PPL jest skończona liczba
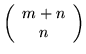 i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
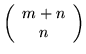 ).
Wykazaliśmy więc
twierdzenie:
).
Wykazaliśmy więc
twierdzenie:
Twierdzenie 3.2
Jeśli algorytm simpleks nie zapętla się
3.2, to rozwiązuje PPL w skończonej
liczbie iteracji. Co więcej, jeśli problem jest
niesprzeczny i ograniczony, to istnieje rozwiązanie bazowe które
jest równocześnie rozwiązaniem optymalnym.
Wśród metod unikania cykliczności elegancją
3.3
wyróżnia się reguła R.G. Blanda [2]
zwana także regułą najmniejszego indeksu.
Reguła Blanda.
- Wybierz jako zmienną wchodzącą tę zmienną która
- (i)
- ma dodatni współczynnik we wzorze na
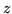 ,
,
- (ii)
- spośród wszystkich zmiennych o dodatnim współczynniku we wzorze
na
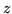 ma najmniejszy indeks.
ma najmniejszy indeks.
- Wybierz jako zmienną wychodzącą tę która
- (iii)
- powoduje najsilniejsze ograniczenie od góry dla zmiennej wchodzącej,
- (iv)
- spośród wszystkich kandydatów na zmienną wychodzącą (tj zmiennych
bazowych spełniających (iii)) ma najmniejszy indeks.
Regułę Blanda można podać nieco bardziej formalnie w sposób następujący.
Niech będzie dany słownik
|
(3.27) |
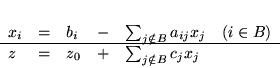 |
(w słowniku (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
) 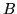 jest zbiorem indeksów zmiennych bazowych).
jest zbiorem indeksów zmiennych bazowych).
- -
- Wybierz jako zmienną wchodzącą
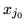 dla której
dla której
- (a)
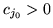
- (b)
-

- -
- Wybierz jako zmienną wychodzącą
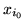 dla której
dla której
- (a)
-
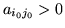
- (b)
-
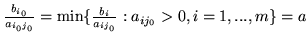
- (c)
-
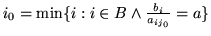
W porównaniu z metodą którą stosowaliśmy do tej pory różnica pojawia się
tylko w punkcie (ii) - stosujemy tę regułe zamiast wybierać zmienną
wchodzącą o największym
współczynniku (dodatnim) w funkcji celu.
Przykład 3.5
Dla słownika
postępując według reguły Blanda wybierzemy
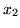
jako zmienną
wchodzącą i
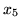
jako zmienną wychodzącą.
Twierdzenie 3.3 (Bland [
2])
Jeśli wybory zmiennych wchodzących i wychodzących w algorytmie
simpleks dokonywane są według reguły Blanda, to algorytm kończy
się po skończonej liczbie iteracji.
Idea dowodu twierdzenia Blanda zaczerpnięta jest z [4].
Dowód. Ze względu na twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wystarczy
wykazać, że jeżeli zmienne wchodząca i wychodząca będą
wybierane według reguły Blanda to nie może wystąpić
cykliczność .
wystarczy
wykazać, że jeżeli zmienne wchodząca i wychodząca będą
wybierane według reguły Blanda to nie może wystąpić
cykliczność .
Dla dowodu nie wprost przypuśćmy, że zmienne są wybierane
regułą Blanda, a jednak algorytm zapętla się.
to znaczy, że poczynając
od pewnego słownika 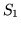 w kolejnych iteracjach otrzymujemy
w kolejnych iteracjach otrzymujemy
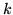 -elementowy ciąg słowników
-elementowy ciąg słowników
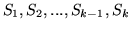 taki,że
taki,że
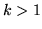 i
i 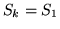 . Oczywiście wszystkie słowniki
. Oczywiście wszystkie słowniki
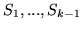 są wtedy zdegenerowane.
są wtedy zdegenerowane.
Zmienną będziemy nazywali błędną3.4 jeżeli dla pewnych słowników spośród
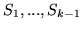 jest zmienną bazową a dla innych niebazową.
jest zmienną bazową a dla innych niebazową.
Przypuśćmy, że 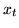 jest zmienną błędną o największym inteksie
jest zmienną błędną o największym inteksie
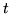 . Niech
. Niech  będzie jednym ze słowników
będzie jednym ze słowników
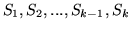 ,
takim, że
,
takim, że 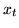 jest zmienną bazową wychodzącą słownika
jest zmienną bazową wychodzącą słownika  i niech
i niech 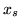 będzie zmienną wchodzącą
będzie zmienną wchodzącą  . Inaczej mówiąc:
. Inaczej mówiąc: 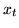 i
i 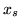 są takie, że
są takie, że
- -
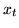 jest zmienną bazową
jest zmienną bazową  i nie jest zmienną bazową
słownika następnego,
i nie jest zmienną bazową
słownika następnego,
- -
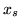 jest zmienną niebazową słownika
jest zmienną niebazową słownika  i bazową słownika
następnego.
i bazową słownika
następnego.
Oznaczmy przez 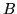 zbiór indeksów zmiennych bazowych słownika
zbiór indeksów zmiennych bazowych słownika  i
powiedzmy, że
i
powiedzmy, że  jest postaci
jest postaci
|
(3.28) |
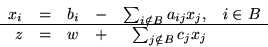 |
Skoro
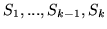 jest cyklem, tzn
jest cyklem, tzn 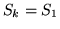 , musi istnieć
inny słownik, nazwijmy go
, musi istnieć
inny słownik, nazwijmy go 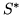 taki, że
taki, że 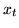 jest zmienną
wchodzącą
jest zmienną
wchodzącą 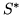 . Z tego samego powodu wartość zmiennej
. Z tego samego powodu wartość zmiennej 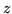 (funkcji
celu) w rozwiązaniu bazowym każdego słownika
(funkcji
celu) w rozwiązaniu bazowym każdego słownika
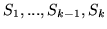 jest taka sama. Tak więc wzór na
jest taka sama. Tak więc wzór na 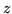 w słowniku
w słowniku 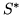 jest postaci
jest postaci
|
(3.29) |
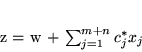 |
przy czym 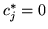 dla
dla 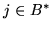 , gdzie
, gdzie 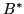 jest zbiorem indeksów
zmiennych bazowych słownika
jest zbiorem indeksów
zmiennych bazowych słownika 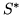 .
Na mocy twierdzenia
.
Na mocy twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , każde rozwiązanie słownika
, każde rozwiązanie słownika  jest także rozwiązaniem słownika
jest także rozwiązaniem słownika 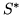 . Jednym z rozwiązań
słownika
. Jednym z rozwiązań
słownika  jest, jak łatwo zauważyć:
jest, jak łatwo zauważyć:
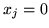 dla wszystkich zmiennych niebazowych
dla wszystkich zmiennych niebazowych  , poza
, poza 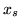 (czyli dla
(czyli dla
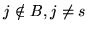 ),
),
-
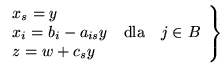 dla dowolnego
dla dowolnego 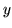 .
.
Wstawiając to rozwiązanie do wzoru (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymamy
) otrzymamy
Stąd
dla każdego 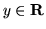 . Wobec dowolności
. Wobec dowolności 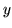 mamy
mamy
|
(3.30) |
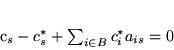 |
- -
- Z faktu, że
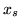 jest zmienną wchodzącą słownika
jest zmienną wchodzącą słownika  wynika, że
wynika, że 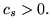
- -
- Przypomnijmy, że
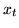 jest błędną zmienną o
największym indeksie. Stąd oczywiście wynika, że
jest błędną zmienną o
największym indeksie. Stąd oczywiście wynika, że 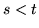 (
(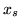 jest także zmienną błędną).
jest także zmienną błędną).
- -
- Skoro
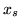 nie jest zmienną wchodzącą w słowniku
nie jest zmienną wchodzącą w słowniku 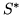 ,
,
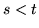 , i wybór zmiennej wchodzącej następuje według
reguły Blanda, mamy
, i wybór zmiennej wchodzącej następuje według
reguły Blanda, mamy 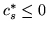 .
.
Ze wzoru (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) wynika więc, że
) wynika więc, że
|
(3.31) |
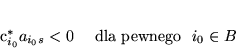 |
Oczywiście 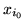 jest zmienną bazową w słowniku
jest zmienną bazową w słowniku  (bo
(bo 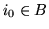 ) i zmienną niebazową w słowniku
) i zmienną niebazową w słowniku
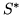 (
(
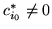 , w przeciwnym przypadku nie
moglibyśmy mieć
, w przeciwnym przypadku nie
moglibyśmy mieć
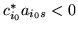 ).
).
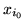 jest więc zmienną błędną i wobec tego
jest więc zmienną błędną i wobec tego
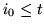 . Co więcej:
. Co więcej: 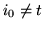 , bowiem
, bowiem 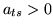 skoro
skoro 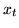 jest zmienną wychodzącą a
jest zmienną wychodzącą a 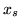 zmienną
wchodzącą słownika
zmienną
wchodzącą słownika  . Pamiętamy, że
. Pamiętamy, że 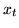 jest
zmienną wchodzącą słownika
jest
zmienną wchodzącą słownika 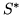 . Wobec tego
. Wobec tego 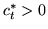 i w konsekwencji
i w konsekwencji 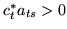 . Ostatecznie
. Ostatecznie 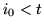 .
.
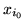 nie jest jednak zmienną wchodzącą słownika
nie jest jednak zmienną wchodzącą słownika 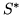 (jest nią przecież
(jest nią przecież 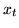 , a właśnie wykazaliśmy,
że
, a właśnie wykazaliśmy,
że 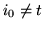 ), a ponieważ zmienną wchodzącą wybieramy
według reguły Blanda, musi być
), a ponieważ zmienną wchodzącą wybieramy
według reguły Blanda, musi być
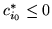 .
Ze wzoru (
.
Ze wzoru (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) mamy więc
) mamy więc 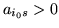 .
.
Z faktu, że 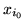 jest błędną zmienną oraz, że
wartość
jest błędną zmienną oraz, że
wartość 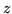 w rozwiązaniu bazowym jest stale równa
w rozwiązaniu bazowym jest stale równa 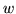 dla wszystkich słowników
dla wszystkich słowników 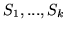 wynika, że
wynika, że
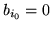 . Tak więc
. Tak więc 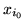 była zmienną
która powinna, według reguły Blanda, być zmienną
wychodzącą ze słownika
była zmienną
która powinna, według reguły Blanda, być zmienną
wychodzącą ze słownika  (
(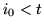 ). Ta sprzeczność
kończy dowód twierdzenia Blanda.
). Ta sprzeczność
kończy dowód twierdzenia Blanda.





Next: Ile jest rozwiązań optymalnych?
Up: Szczegóły metody
Previous: Czy simpleks może się
Spis rzeczy
Indeks
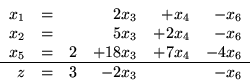
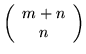 .
Tak więc słowników dla danego PPL jest skończona liczba
.
Tak więc słowników dla danego PPL jest skończona liczba
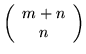 i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
i jeśli w każdej iteracji otrzymujemy inny słownik, wtedy algorytm simpleks
musi nas doprowadzić do rozwiązania problemu w skończonej liczbie
iteracji (co najwyżej
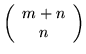 ).
Wykazaliśmy więc
twierdzenie:
).
Wykazaliśmy więc
twierdzenie:
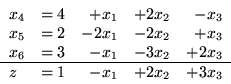
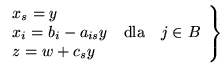 dla dowolnego
dla dowolnego