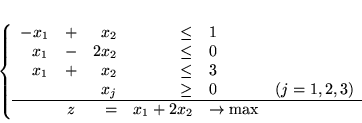Next: Interpretacja ekonomiczna
Up: Korzyści
Previous: Korzyści
Spis rzeczy
Indeks
Niech będzie dany problem prymalny
|
(4.14) |
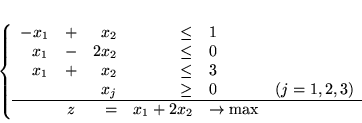 |
Wykażemy, że
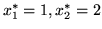 jest rozwiązaniem optymalnym problemu (
jest rozwiązaniem optymalnym problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Problemem dualnym do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest
) jest
|
(4.15) |
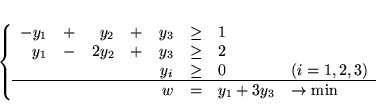 |
Oznaczmy przez
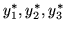 optymalne rozwiązania problemu (
optymalne rozwiązania problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Zauważmy, że
- -
-
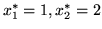 jest rozwiązaniem dopuszczalnym problemu (
jest rozwiązaniem dopuszczalnym problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
- -
- Spośród trzech pierwszych nierówności problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
) 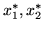 spełnia drugą jako nierówność silną
(
spełnia drugą jako nierówność silną
(
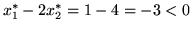 ), a więc, na mocy twierdzenia
), a więc, na mocy twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ,
, 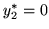 .
.
- -
- Ponieważ
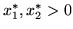 , na mocy twierdzenia
, na mocy twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) obie nierówności
w problemie (
obie nierówności
w problemie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są równościami, otrzymujemy więc
) są równościami, otrzymujemy więc
i stąd
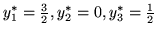 .
Ponieważ
.
Ponieważ
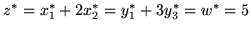 ,
,
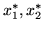 jest rozwiązaniem optymalnym (
jest rozwiązaniem optymalnym (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
zaś
)
zaś
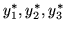 rozwiązaniem optymalnym (
rozwiązaniem optymalnym (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).