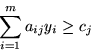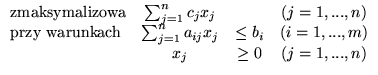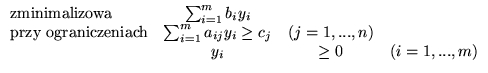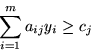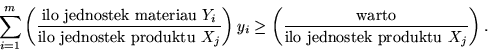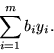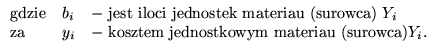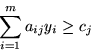Interpretacja ekonomiczna zmiennych dualnych

Problemem praktycznym który modeluje PPL
$\begin{array}{lccc} \mbox{zmaksymalizować} & \su... ...{ij}x_j & \leq b_i & (i=1,...,m)\\ & x_j & \geq 0 &(j=1,...,n) \end{array}$
jest następujące zagadnienie ekonomiczne.
Firma $F$ produkuje towary $X_1,...,X_n$. Do wyprodukowania tych towarów potrzebne są materiały (surowce) $Y_1,...,Y_m$ w ilości $a_{ij}$ jednostek materiału $Y_i$ na jednostkę towaru $X_j$ dla $i=1,...,m$, $j=1,...,n$. Firma dysponuje $b_i$ jednostkami materiału $Y_i$ dla $i=1,...,m$. Zysk z produkcji jednej jednostki towaru $X_j$ wynosi $c_j$ (ten zysk jednostkowy może być ujemny co dla firmy oznacza oczywiście stratę).
Ta ekonomiczna interpretacja problemu prymalnego jest dość oczywista. Interpretacja problemu dualnego
$\begin{array}{lccc} \mbox{zminimalizować} &\sum^... ..._{ij}y_i \geq c_j & (j=1,...,n)\\ & y_i & \geq 0 & (i=1,...,m) \end{array}$
jest mniej jasna. Inspirująca jest tutaj kwestia zgodności jednostek fizycznych^4.2 (p. [13]). W ograniczeniach

$$\sum^m_{i=1}a_{ij}y_i \geq c_j$$

po prawej stronie nierówności jednostką fizyczną jest wartość jednostki produktu, jednostkowy zysk. Jednostkami $a_{ij}$ są zaś ilości jednostek materiału $Y_i$ potrzebnego do wytworzenia jednostki produktu $X_j$, czyli

$$\sum^m_{i=1} \left( \frac{\mbox{ilość jednostek materiału }... ...mbox{wartość}}{\mbox{ilość jednostek produktu } X_j} \right).$$

Stąd jednostką fizyczną zmiennej dualnej $y_i$ musi być

$$\left( \frac{\mbox{wartość}}{\mbox{ilość jednostek materiału } Y_i} \right).$$

W problemie dualnym minimalizujemy dualną funkcję celu

$$\sum^m_{i=1}b_iy_i.$$

Zmienne dualne $y_1,...,y_m$ interpretujemy jako koszty jednostki materiałow $Y_1,...,Y_m$. W ten sposób dualna funkcja celu $\sum^m_{i=1}b_iy_i$ jest sumą składników postaci $b_iy_i$
$\begin{array}{lll} \mbox{gdzie} & b_i & - \mbox{ jest ilością jednostek mate... ... & y_i & - \mbox{ kosztem jednostkowym materiału (surowca)} Y_i. \end{array}$
Fakt, że w problemie dualnym poszukujemy minimum $\sum^m_{i=1}b_iy_j$ oznacza, że szukamy wartości $y_i$ przy których nakład (koszt materiałów (surowców)) jest minimalny.
W dualnych ograniczeniach lewa strona wzoru

$$\sum^m_{i=1}a_{ij}y_i \geq c_j$$

oznacza wtedy koszty produkcji towaru $X_j$. Mamy tu bowiem sumę iloczynów

(ilość jednostek materiału $Y_i$ potrzebnych do wytworzenia jednostki $X_j$)$\cdot$ (koszt jednostkowy $Y_j$)

która, jak zakładamy, jest co najmniej równa $c_j$ - jednostkowej wartości produktu $X_j$.
Zmienne dualne $y_i, \ (i=1,...,m)$ nazywane są często cenami dualnymi.
Zauważmy jednak, że cena dualna ma niewiele wspólnego z "prawdziwąeną surowca. Z twierdzenia o odstępach komplementarnych wynika, że gdy dla pewnego $i$ w rozwiązaniu optymalnym $(x_1^*, ..., x_n^*)$ zachodzi
$\sum_{j=1}^n a_{ij}x_j^* < c_i$, czyli surowca $Y_i$ jest zbyt dużo, to cena dualna tego surowca jest równa zero.
Dodatkowym uzasadnieniem interpretacji zmiennych dualnych jest następujące twierdzenie (które podajemy tu bez dowodu).

Twierdzenie 4.7   Jeżeli problem prymalny

$$\begin{array}{lcll} \sum^n_{j=1}a_{ij}x_j & \leq & b_i & ... ...e \sum^n_{j=1}c_jx_j & \rightarrow & \mbox{max} \end{array}$$ (4.16)

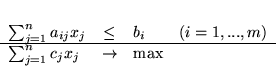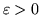
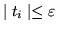
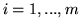
ma niezdegenerowane bazowe rozwiązanie optymalne, to istnieje $\varepsilon > 0$ takie, że jeśli $\mid t_i \mid \leq \varepsilon$ dla $i=1,...,m$, to problem

$$\begin{array}{lcll} \sum^n_{j=1}a_{ij} & \leq & b_i +t_i &... ...e \sum^n_{j=1}c_jx_j & \rightarrow & \mbox{max} \end{array}$$

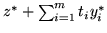
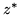
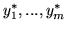
ma rozwiązanie optymalne o wartości $z^*+\sum^m_{i=1}t_iy^*_i$, gdzie $z^*$ jest wartością optymalną problemu (), zaś $y^*_1,...,y^*_m$ optymalnym rozwiązaniem dla problemu dualnego.