$n=2$

Przyjrzyjmy się poniższemu przykładowi.

Przykład 7.1  

$$% latex2html id marker 8630 \begin{array}{lrcrcr} \mbox{z... ... & x_1 &&& \leq & 3\\ &&& x_1,x_2 & \geq & 0 \end{array}$$

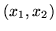
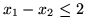
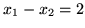
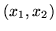
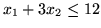
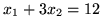
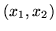
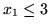
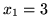
Zbiór punktów $(x_1,x_2)$ płaszczyzny spełniających warunek $x_1 - x_2 \leq 2$ to wszystkie punkty płaszczyzny leżące nad prostą $x_1-x_2=2$, punkty $(x_1,x_2)$ spełniające $x_1+3x_2 \leq 12$ to wszystkie punkty leżące poniżej prostej $x_1+3x_2=12$, zbiór punktów $(x_1,x_2)$ spełniających $x_1 \leq 3$ to punkty na lewo od prostej $x_1=3$ (oczywiście w każdym przypadku włacznie z punktami leżącymi na odpowiedniej prostej. 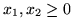Ograniczenia $x_1,x_2 \geq 0$ oznaczają, że chodzi nam o punkty pierwszej ćwiartki.
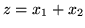
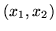
Tak więc szukać będziemy maksimum funkcji $z=x_1+x_2$ dla $(x_1,x_2)$ należących do wielokąta ograniczonego prostymi: $x_1-x_2=2, \ \ x_1+3x_2=12, \ \ x_1=0, \ \ x_1=3, \ \ x_2=0$ (rys. ).

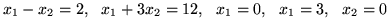
Rys.6.1

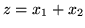
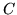
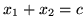
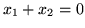
Maksymalizacja funkcji $z=x_1+x_2$ oznacza, że powinniśmy znaleźć taką maksymalną stała $C$, żeby prosta $x_1+x_2=c$ miała co najmniej jeden punkt wspólny z naszym wielobokiem. Inaczej mówiąc, musimy prostą $x_1+x_2=0$ przesunąć równolegle najwyżej jak to możliwe, tak jednak aby miała z wielobokiem przecięcie niepuste. Jest jasne, że optymalne położenie prostej będzie takie, w którym jedynym punktem wspólnym prostej i wieloboku będzie $P=(3,3)$. 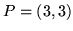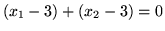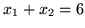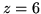Prosta będzie miała równanie $(x_1 - 3) +( x_2 - 3) = 0$, a więc $x_1 + x_2= 6$ i wartość maksymalna $z = 6$.$\Box$

Zauważmy przy okazji, że z sytuacją więcej niż jednego rozwiązania będziemy mieli do czynienia w pewien sposób rzadko: odpowiedni bok wieloboku będzie musiał być równolegly do prostej reprezentującej funkcję celu. Zbiór rozwiązań optymalnych będzie wtedy nie punktem jak w przykładzie , a zbiorem punktów pewnego odcinka (boku wieloboku).
Dla ograniczeń zadanych w przykładzie będzie tak na przykład wtedy, gdy funkcja celu będzie zadana wzorem $z=x_1+3x_2$. Wtedy zbiorem rozwiązań optymalnych będzie odcinek łączący punkty $(0,4)$ i $(3,3)$, a wartością optymalnę $z=12$.