Przykład 7.2
Dla
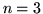
przykład Klee-Minty'ego wygląda następująco:
Czytelnik który wykonał ćwiczenie
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
otrzymał osiem słowników i tyleż
rozwiązań bazowych:
(trzy współrzędne tych rozwiązań odpowiadają zmiennym decyzyjnym
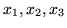
podczas gdy trzy następne zmiennym sztucznym
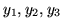
).
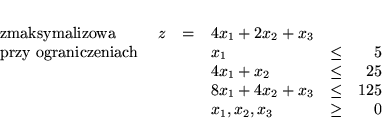
![\begin{displaymath}{\bf x^1}= \left[ \begin{array}{r}
0\\ 0\\ 0\\ 5\\ 25 \\ 125...
...begin{array}{r}
0\\ 25\\ 0\\ 0\\ 0 \\ 125
\end{array} \right]\end{displaymath}](img776.gif)
![\begin{displaymath}
{\bf x^5}= \left[ \begin{array}{r}
0\\ 25\\ 25\\ 5\\ 0 \\ ...
...gin{array}{r}
0\\ 0\\ 125\\ 5\\ 25 \\ 0
\end{array} \right]
\end{displaymath}](img777.gif)
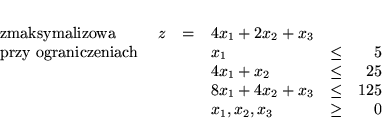
![\begin{displaymath}{\bf x^1}= \left[ \begin{array}{r}
0\\ 0\\ 0\\ 5\\ 25 \\ 125...
...begin{array}{r}
0\\ 25\\ 0\\ 0\\ 0 \\ 125
\end{array} \right]\end{displaymath}](img776.gif)
![\begin{displaymath}
{\bf x^5}= \left[ \begin{array}{r}
0\\ 25\\ 25\\ 5\\ 0 \\ ...
...gin{array}{r}
0\\ 0\\ 125\\ 5\\ 25 \\ 0
\end{array} \right]
\end{displaymath}](img777.gif)