




Next: Powłoki wypukłe zbiorów
Up: Interpretacja geometryczna
Previous: n=3
Spis rzeczy
Indeks
Komentarz
W większości książek poświęconych programowaniu liniowemu interpretacja
geometryczna prezentowana jest na samym początku, zaraz po przedstawieniu problemu
programowania liniowego lub algorytmu sympleks
(por. [10], [17], [21]). Taka
metoda dydaktyczna ma dużo zalet. Interpretacja geometryczna jest
bowiem bardzo prosta i daje dobre
intuicje. Niemniej, w tym bardzo pożytecznym geometrycznym
ujęciu kryje się pewna pułapka.
Sugeruje ono, że wszystko jest tu bardzo proste i łatwe do zobaczenia i
narysowania. Tymczasem wcale tak
nie jest. Narysować i wyobrazić sobie można jedynie przestrzenie
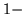 ,
, 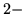 i
i 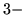 wymiarowe. Próby -
niewiedzieć czemu bardzo modne - wyobrażenia sobie przestrzeni więcej
niż
wymiarowe. Próby -
niewiedzieć czemu bardzo modne - wyobrażenia sobie przestrzeni więcej
niż 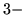 wymiarowych
7.1
są z góry skazane na niepowodzenie z prostego powodu:
przestrzeń
wymiarowych
7.1
są z góry skazane na niepowodzenie z prostego powodu:
przestrzeń 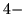 (i więcej) wymiarowa nie ma swojej
interpretacji geometrycznej w przestrzeniach mniej wymiarowych
7.2.
(i więcej) wymiarowa nie ma swojej
interpretacji geometrycznej w przestrzeniach mniej wymiarowych
7.2. 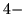 wymiarowa przestrzeń w której
czwartym wymiarem jest czasnie stanowi tu zadnej pomocy.
Przestrzen
wymiarowa przestrzeń w której
czwartym wymiarem jest czasnie stanowi tu zadnej pomocy.
Przestrzen 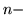 wymiarowa jest dla
wymiarowa jest dla 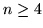 pojęciem czysto algebraicznym. Fakt, że język tu używany jest zapożyczony z geometrii
daje nam tyle, że w naszej wyobraźni jesteśmy w stanie kreować
obrazy - interpretacje w przestrzeniach
tej wyobraźni dostępnych, czyli
pojęciem czysto algebraicznym. Fakt, że język tu używany jest zapożyczony z geometrii
daje nam tyle, że w naszej wyobraźni jesteśmy w stanie kreować
obrazy - interpretacje w przestrzeniach
tej wyobraźni dostępnych, czyli 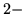 i
i 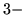 wymiarowych.
wymiarowych.





Next: Powłoki wypukłe zbiorów
Up: Interpretacja geometryczna
Previous: n=3
Spis rzeczy
Indeks