




Next: Problem programowania liniowego
Up: Wstęp
Previous: Po co ten skrypt?
Spis rzeczy
Indeks
Programowanie liniowe jest szczegolnym zagadnieniem
programowania matematycznego.
Ogólny problem programowania matematycznego
1.1
można sformułować następująco:
Niech 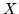 będzie dowolnym zbiorem i niech
będzie dowolnym zbiorem i niech 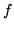 bedzie funkcją zdefiniowana
w zbiorze
bedzie funkcją zdefiniowana
w zbiorze 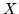 o wartościach w zbiorze liczb rzeczywistch.
Znajdź wartość maksymalną
o wartościach w zbiorze liczb rzeczywistch.
Znajdź wartość maksymalną 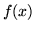 dla
dla 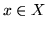 .
.
Będziemy pisać krótko:
-
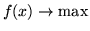
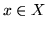
W przypadku programowania liniowego o zbiorze 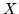 zakładamy,
że jest podzbiorem
zakładamy,
że jest podzbiorem 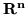 zdefiniowanym przez układ nierówności liniowych,
zaś funkcja
zdefiniowanym przez układ nierówności liniowych,
zaś funkcja 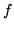 jest funkcją liniową.
jest funkcją liniową.
Rozdziały 2-6 są poświęcone samemu programowaniu liniowemu.
Kolejno więc przedstawiona jest
metoda sympleks (rozdział 3), zasada dualności (rozdział 4),
zredukowana metoda sympleks
(rozdział 4). W rozdziale 6 omówiona jest szczególna sytuacja zadania ograniczonego.
Pozostałe rozdziały to interpretacje i zastosowania
geometryczne programowania liniowego
(rozdział 7) i metody sieciowe z przykładami ich zastosowań w teorii
grafów (rozdział (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Podrozdziały 1 i 2 rozdziału siódmego w których jest mowa
o interpretacji programowania liniowego w przypadkach dwu- i trzy-wymiarowym mogą
być czytane znacznie
wcześniej niż występują w tekście, po opisie metody sympleks - a więc
po rozdziale trzecim.
). Podrozdziały 1 i 2 rozdziału siódmego w których jest mowa
o interpretacji programowania liniowego w przypadkach dwu- i trzy-wymiarowym mogą
być czytane znacznie
wcześniej niż występują w tekście, po opisie metody sympleks - a więc
po rozdziale trzecim.
Poświęcony przepływom w sieciach rozdział 8 jest zawarty w skrypcie
z dwóch powodów. Powodem pierwszym jest fakt, że choć metoda
sieci rozwiązuje tylko pewien szczególny problem programowania liniowego,
niemniej dla tego szczególnego problemu algorytm sieciowy jest szybszy.
Po drugie, otrzymujemy w ten sposób okazję do przedstawienia pięknego
twierdzenia o maksymalnym przepływie i minimalnym przekroju.
Ważne wnioski z tego twierdzenia: twierdzenia Halla, Königa-Egerváry'ego
i Mengera dowodzą jak głębokim wynikiem jest twierdzenie o maksymalnym
przepływie i minimalnym przekroju. Zobaczymy także, że
twierdzenie to jest konsekwencją zasady dualności.
Maszynopisy pierwszych wersji tego skryptu były udostępnione
studentom trzeciego roku Wydziału Matematyki Stosowanej AGH
w latach 2000/2001 i 2001/2002. Kolejne wersje książki
były dostępne także na stronie www WMS AGH. Studentom oraz współpracującym ze
mną dr Irminie Zioło i mgr Anecie Dudek dziękuję za cenne uwagi które
pozwoliły mi usunąć wiele błędów w poprzednich wersjach.
Mimo naszych starań z pewnością pozostały w tej książce pomyłki lub błędy.
Będę wdzięczny za ich wskazanie. Korespondencję proszę kierować
na adres elektroniczny.
W latach 2000-2002 poza wykładami dla studentów Wydziału
Matematyki Stosowanej AGH prowadziłem także wykład z programowania liniowego dla
studentów MIAGE1.2
na uniwersytecie w Orleanie. Dziekuję profesorom Gerard Ferrand i Henri Thuillier
za cenne rady, zaś Aleksowi Tessier za perfekcyjnie prowadzone ćwiczenia.
Pozostaje mi wyjaśnić znaczenie dwóch tajemniczych znaczków pojawiających
się w różnych miejscach tekstu: i  . oznacza,
ze coś definitywnie się skończyło, najczęściej jest to znak końca dowodu
twierdzenia (lub sygnał, że z jakiegoś powodu dowodu w ogóle nie będzie),
czasami koniec przykładu.
. oznacza,
ze coś definitywnie się skończyło, najczęściej jest to znak końca dowodu
twierdzenia (lub sygnał, że z jakiegoś powodu dowodu w ogóle nie będzie),
czasami koniec przykładu.  występuje wtedy gdy na chwile porzucamy coś
(na ogół przykład) do czego jeszcze wrócimy.
występuje wtedy gdy na chwile porzucamy coś
(na ogół przykład) do czego jeszcze wrócimy.
Adam Paweł Wojda
wojda@uci.agh.edu.pl
Kraków, styczeń, 2003





Next: Problem programowania liniowego
Up: Wstęp
Previous: Po co ten skrypt?
Spis rzeczy
Indeks