- ... matematycznego1.1
- Warto zauważyć i zapamiętać tę
definicję, szczególnie wobec faktu, że słowo programowanie
występuje także w znaczeniu bardzo różnym od rozważanego
w bliskiej matematyce informatyce.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... MIAGE1.2
- Methodes Informatiques en Géstion et Economie
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kg2.1
-
To po to by Ola nie musiała jeść zbyt dużo marchewki
z chlebem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... słownika3.1
- Można wykazać,
że PPL w którym występuje zjawisko cykliczności musi mieć co najmniej 7 zmiennych
decyzyjnych. Przykład Chvátala jest więc, w pewnym sensie
najmniejszym PPL który zapętla się.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... się3.2
- Inaczej: jeśli nie
występuje zjawisko cykliczności.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elegancją3.3
- elegancja (mat.) = prostota (wulg.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...błędną3.4
- Tu błędna
nie pochodzi od słowa błąd a raczej od
błędnego rycerza lub błędnego ognika.
Taka co to raz jest a raz jej nie ma - w
ogóle nie wie czego chce.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zmiennych3.5
- Sprawdź sam jeśli nie wierzysz!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... na\-stę\-pu\-ją\-co3.6
- Wyjątkowo w tym przypadku, wygodniej nam będzie oznaczać zmienne sztuczne
przez
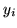 zamiast, jak to było zawsze do tej pory, przez
zamiast, jak to było zawsze do tej pory, przez 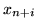 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... niewiadomymi4.1
-
Pamiętamy z dowodu twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , że w najgorszym przypadku
iteracji może być
, że w najgorszym przypadku
iteracji może być
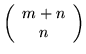 w pierwszym i
w pierwszym i
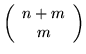 drugim przypadku, a więc tyle samo
drugim przypadku, a więc tyle samo
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fizycznych4.2
- W tym fragmencie tekstu słowo jednostka
występuje w dwóch zupełnie różnych znaczeniach.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
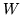 4.3
4.3
- Pozostałe zbiory indeksów też zostały
nazwane tak, by było je można łatwiej zapamiętać:
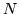 od nierówność,
od nierówność, 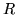 od
równość,
od
równość, 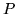 od pozytywne (tu w znaczeniu: nieujemne).
od pozytywne (tu w znaczeniu: nieujemne).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bazową5.1
- Macierz bazową czasami wygodnie jest oznaczać przez
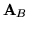 (by podkreślić, że powstała z macierzy
(by podkreślić, że powstała z macierzy 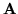 ), a czasami przez
), a czasami przez 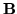 (bo krócej).
(bo krócej).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)5.2
- Nigdy nie obliczamy
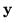 przez
wyliczenie macierzy
przez
wyliczenie macierzy 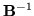 co jest wysiłkiem dużym i zupełnie zbędnym.
Szczególnie wtedy, gdybyśmy chcieli w tym celu wykorzystać zupełnie nieefektywną
metodę wyznacznikową.
co jest wysiłkiem dużym i zupełnie zbędnym.
Szczególnie wtedy, gdybyśmy chcieli w tym celu wykorzystać zupełnie nieefektywną
metodę wyznacznikową.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
pusty5.3
- Na mocy definicji przyjmujemy
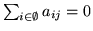 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ma)6.1
- Jeżeli dolne ograniczenia są skończone, to można zmienne
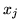 zastąpić
nowymi zmiennymi
zastąpić
nowymi zmiennymi 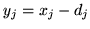 i przyjąć standardowe ograniczenia
i przyjąć standardowe ograniczenia 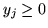 (por. Gass [10]). Ograniczenia od góry na poszczególne zmienne w praktyce
występują prawie zawsze. Na przykład, jeśli zmienne
(por. Gass [10]). Ograniczenia od góry na poszczególne zmienne w praktyce
występują prawie zawsze. Na przykład, jeśli zmienne 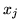 oznaczają wielkość produktów
oznaczają wielkość produktów
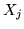 ,
, 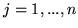 , to górne ograniczenia mogą oznaczać popyt na odpowiednie produkty.
, to górne ograniczenia mogą oznaczać popyt na odpowiednie produkty.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ogra\-ni\-cze\-niom6.2
- W metodzie sympleks z którą obcujemy od trzeciego rozdziału przyjmujemy
wartość
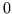 dla zmiennych niebazowych, a więc także wartość indywidualnego
ograniczenia (dolnego, innego nie bylo) na zmienne.
dla zmiennych niebazowych, a więc także wartość indywidualnego
ograniczenia (dolnego, innego nie bylo) na zmienne.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... są6.3
- właściwie mogą być
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...wy\-mia\-ro\-wych
7.1
- Chvatál w swojej książce [4] tak pisze na ten
temat: ... do not try to visualize
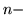 dimentional objects for
dimentional objects for 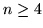 . Such an effort is not only doomed to failure - it may be dangerous
to your mantional health. (If you do succeed, then you are in trouble).
. Such an effort is not only doomed to failure - it may be dangerous
to your mantional health. (If you do succeed, then you are in trouble).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wymiarowych7.2
- Bardziej dobitnie i prosto: przestrzeń
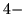 wymiarowa nie jest
wymiarowa nie jest
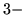 wymiarowa
wymiarowa
(bo 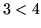 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...wypukły
7.3
- Zbiory wypukłe odgrywają ważną rolę
w wielu działach matematyki, szczególnie w analizie funkcjonalnej
(por. [1]) i optymalizacji (por.
[11]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
beznadziejny8.1
- Jeszcze raz podkreślmy, co znaczy to teoretycznie:
sympleks jest
algorytmem niewielomianowym jak wykazuje przykład Klee-Minty'ego,
w praktycznych zaś przykładach spisuje się bardzo dobrze.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nazywamy8.2
- Niekonsekwentnie...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
łuków8.3
- Na przykład gdy będziemy myśleli o sieciach wodociągowych, kanalizacyjnych
- ale także, czasami, drogowych.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... łuków8.4
- Na przykład dla sieci
komunikacyjnej.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... łuków8.5
- W sieci komunikacyjnej: gdy myślimy raczej o cenie biletu niż odległości.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... łukach8.6
- W praktyce oznacza to, że woda nie płynie jak nie ma rury.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zmiennej8.7
- Gorąco
doradzam rozwiązanie ćwiczenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) właśnie teraz!
właśnie teraz!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... powiększająca8.8
- Dokładniej ścieżka powiększająca
(z którą zetknęliśmy się już w dowodzie twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) to ścieżka z
) to ścieżka z 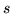 do
do 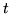 - właśnie przeszliśmy
po niej pod prąd.
- właśnie przeszliśmy
po niej pod prąd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... całkowity8.9
- Jako
pierwszy przepływ można przyjąć przepływ zerowy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rzeczywisty8.10
- Kłopot tylko teoretyczny. Dość trudno sobie
wyobrazić zadanie praktyczne w którym niezbędne byłoby uwzględnianie
ograniczeń niewymiernych na przepustowość łuków.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
podział8.11
- Przypomnijmy, że zbiory
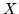 i
i 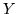 są podziałem
są podziałem
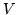 jeżeli
jeżeli 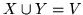 i
i
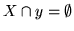 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
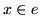 8.12
8.12
- Zwrócić tu anleży uwagę
na subtelną różnicę pomiędzy pełnym skojarzeniem w grafie zwykłym i pełnym
skojarzeniem
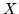 w
w 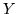 w grafie dwudzielnym
w grafie dwudzielnym 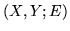 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sieci8.13
- Zauważmy, że
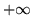 w definicji
przepustowości łuków sieci
w definicji
przepustowości łuków sieci  można zastąpić wystarczająco dużymi liczbami
całkowitymi
(na przykład
można zastąpić wystarczająco dużymi liczbami
całkowitymi
(na przykład 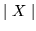 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
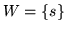 8.14
8.14
-
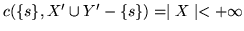 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... senacie8.15
- Także Senacie Akademii Górniczo-Hutniczej.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... problemami8.16
- W Senacie AGH są to Komisje
do Spraw Kształcenia, Naukowa, Budżetowa i inne.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... grafów8.17
- Z pewnością powodów gwałtownego rozwoju teorii grafów
było z pewnością wiele (np. znany problem czterech kolorów, liczne zastosowania
(w tym w informatyce)). Niewątpliwie jednak książka Königa odegrała w tym rozwoju
dużą rolę.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... problemu8.18
- Zauważmy, że ograniczenia
przepustowości wierzchołków mogą występować w zagadnieniach praktycznych.
W sieciach komunikacyjnych często wierzchołki oznaczają
skrzyżowania ulic. Jest oczywiste, że
możliwość wprowadzenia ograniczeń przepustowości wierzchołków - skrzyżowań
jest tu bardzo istotna.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
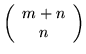 w pierwszym i
w pierwszym i
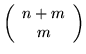 drugim przypadku, a więc tyle samo
drugim przypadku, a więc tyle samo