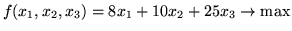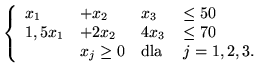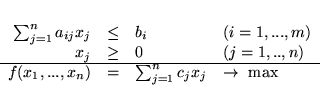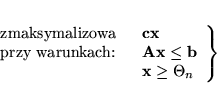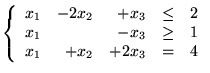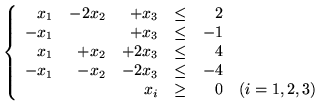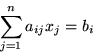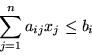Przykład 2.1
Właściciel ciężarówki może przewieźć z miejscowości
A do
B
cukier, mąkę i chipsy. W ciężarówce mieści się towar o objętości
co najwyżej 7000 litrów i wadze co najwyżej 5 ton. 1 kg cukru zajmuje
objętość 1,5 litra, 1 kg mąki 2 litry, natomiast 1 kg chipsów zajmuje
objętość 4 litrów. Zysk od przewozu poszczególnych towarów jest
następujący:
- -
- za 100 kg cukru 8 zł,
- -
- za 100 kg mąki 10 zł,
- -
- za 100 kg chipsów 25 zł.
Ile cukru, mąki i chipsów powinien załadować właściciel ciężarówki
aby zmaksymalizować swój zysk?
Matematyczny model tak postawionego zadania jest następujący:
Oznaczmy przez:
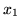 - ilość cukru,
- ilość cukru,
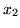 - ilość mąki,
- ilość mąki,
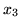 - ilość chipsów
- ilość chipsów
(za każdym razem w setkach kilogramów).
Skoro ciężarówka może zabrać co najwyżej 5 ton towarów,
musi zachodzić nierówność:
Z kolei ograniczenie objętości wyraża się wzorem
Zysk właściciela wynosi:
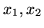
i
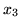
muszą być oczywiście nieujemne.
Po uproszczeniach otrzymamy więc problem programowania matematycznego:
-
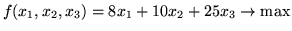
- w zbiorze
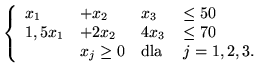
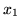 - ilość cukru,
- ilość cukru,
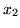 - ilość mąki,
- ilość mąki,
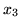 - ilość chipsów
- ilość chipsów