Algorytm Forda-Fulkersona

Niech $S=(V,A;c)$ będzie siecią a $f$ przepływem w $S$ - jeśli nie mamy lepszego, może to być przepływ zerowy, tj. przepływ równy zero na wszystkich łukach sieci . Algorytm - wykorzystujący ideę dowodu twierdzenia polega na cechowaniu wierzchołków sieci cechami postaci $(x^-,\varepsilon )$ lub $(x^+,\varepsilon )$ oraz modyfikacji przepływu jeśli $f$ okazał się przepływem który nie jest maksymalny lub znalezieniu przekroju o przepustowości równej wartości przepływu $f$.
Cechowanie. Wierzchołkowi $s$ nadajemy cechę $(-,\infty )$.
Niech $x$ będzie wierzchołkiem ocechowanym. Z wierzchołka $x$ cechujemy nieocechowane jeszcze wierzchołki w jednej z dwóch sytuacji:

(a)

jeśli istnieje wierzchołek nieocechowany $y$ taki, że $(x,y)\in A$ i $f(x,y) < c(x,y)$ to wierzchołkowi $y$ nadajemy cechę $(x^+,\varepsilon (y))$, gdzie $\varepsilon (y)=\mbox{min}\{\varepsilon (x), c(x,y)-f(x,y)\}$,

(b)

jeśli istnieje nieocechowany wierzchołek $y$ taki, że $(y,x) \in A$ i $f(y,x)> 0$ to wierzchołkowi $y$ nadajemy cechę $(x^-,\varepsilon(y))$, gdzie $\varepsilon (y)= \mbox{min}\{ \varepsilon (x), f(y,x)\}$

Postępowanie cechowania kończy się jeżeli został ocechowany odpływ $t$ lub nie ocechowano $t$ lecz procesu cechowania nie da się kontynuować (żadnego jeszcze nieocechowanego wierzchołka nie da się już ocechować).

(i)

Jeżeli ocechowaliśmy wierzchołek $t$ to $t$ otrzymał cechę postaci $(x^+,\varepsilon )$ lub $(x^-,\varepsilon )$ (dla pewnego $x\in V$).
W pierwszym przypadku modyfikujemy przepływ na łuku $(x,y)$ wzorem $\tilde{f}(x,t)=f(x,t)=\varepsilon$, w drugim $\tilde{f}(t,x)=f(t,x)-\varepsilon$.
Wierzchołek $x$ jest ocechowany. Jeżeli pierwszy element jego cechy jest postaci $y^+$ to do przepływu na łuku $(y,x)$ dodajemy $\varepsilon$, jeżeli jest to $y^-$ od przepływu na łuku $(x,y)$ odejmujemy $\varepsilon$.
Powtarzając tę czynność odpowiednią liczbę razy dojdziemy e końcu do źródła $s$. Dojdziemy wzdłóż wskazanej przez pierwsze elementy cech wierzchołków ścieżkę zwaną ścieżką powiększającą^8.8. Oczywiście wartość nowego przepływu $\tilde{f}$ wynosi $w(f)+\varepsilon>w(f)$. Proces cechowania rozpoczynamy od nowa przyjmując jako wyjściowy przepływ $\tilde{f}$.

(ii)

Przypuśćmy, że w procesie cechowania nie udało się ocechować wierzchołka $t$, a żadnego nowego wierzchołka nie da się już ocechować. Jest oczywistym, że jeżeli przez $W$ oznaczymy zbiór wierzchołków ocechowanych to $(W,\bar{W})$ jest przekrojem rozdzielającym $s$ od $t$. Co więcej, dla wszystkich $x \in W$ i $y \in \bar{W}$ spełniających $(x,y)\in A$ zachodzi $f(x,y)=c(x,y)$, a jeśli $(y,x) \in A$ to $f(y,x)=0$. Na podstawie uwagi otrzymamy

$$w(f)= \sum_{x\in W\\ y \in \bar{W}}f(x,y) -\sum_{x\in W, y ... ...}f(y,x) = \sum_{x \in W, y\in \bar{W}}c(x,y) = c(W,\bar{W})$$

Na mocy uwagi oznacza to, że przepływ $f$ jest przepływem maksymalnym.

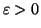
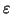
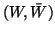
Uwaga 8.3   Zauważmy, że jeśli przepływ nie jest maksymalny, przy pomocy algorytmu Forda-Fulkersona możemy go zwiększyc o $\varepsilon > 0$. Ponieważ w przypadku całkowitych ograniczeń przepustowości i $\varepsilon$ jest całkowite a wartość przepływu ograniczona jest od góry przez $c(W,\bar{W})$ (gdzie $(W,\bar{W})$ jest dowolnym przekrojem), algorytm ten pozwala wtedy znależć przepływ maksymalny. Podobnie jest jeśli przepustowości są liczbami wymiernymi (wtedy problem możnz przekształcić w problem równoważny o przepustowościach całkowitych mnożąc po prostu przepustowości wszystkich łuków przez ich wspólny mianownik).