Metody sieciowe

Problemy które będziemy rozwiązywali przy pomocy metod sieciowych są w rzeczywistości specjalnymi problemami programowania liniowego. Powstać może więc pytanie: czy przypadkiem nie wyważamy otwartych drzwi? Po co szukać specjalnych metod do rozwiązywania specjalnych przypadków, skoro umiemy rozwiązywać przypadek ogólny?
Jest kilka ważnych powodów zajmowania się metodami sieciowymi. Wspomnijmy kilka z nich.

1. Sieci i grafy są wyjątkowo wdzięcznym i działającym na wyobraźnię narzędziem pozwalającym łatwo modelować wiele zagadnień. Jeśli mamy obliczyć sprawność - czyli przepustowość - sieci komunikacyjnej, wodociągowej czy kanalizacyjnej, to wygodniej nam i łatwiej w języku i modelu sieci pozostać niż przechodzić na język równań i nierówności.
2. Algorytmy sieciowe (grafowe) dotyczące omawianych zagadnień są szybsze (o co nietrudno, skoro sympleks - przynajmniej teoretycznie jest, jak widzieliśmy w ustępie , beznadziejny^8.1).
3. Zobaczymy, że jeśli tylko współczynniki macierzy ograniczeń są całkowite to i rozwiązania otrzymane metodami sieciowymi są całkowite.

Pierwszy z powyższych argumentów ma charakter estetyczny i poznawczy. Zajmiemy się nie tylko eleganckimi i matematycznie ładnymi metodami, ale zobaczymy czemu to odpowiada dualność w sieciach (póki nie mamy formalnej defincji sieci należy sobie wyobrażać pod słowem sieć sieć wodociągową Krakowa (p. [13])
Drugi argument ma charakter praktyczny, osłabiony przez wspomniane dobre spisywanie się sympleksu w praktyce.
Argument o całkowitości rozwiązań których to sympleks (czy inny algorytm programowania liniowego) może nie znajdować, dając nam w zamian optymalne ale niecałkowite rozwiązanie, jest ogromnie ważny zarówno z teoretycznego jaki praktycznego względu. Jeśli zmienna 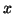$x$ oznacza liczbę pociągów towarowych które trzeba wysłać z Hiszpanii do Władywostoku, rozwiązanie w którym 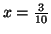$x=\frac{3}{10}$ może być praktycznie nieużyteczne. Zobaczymy także problem kojarzenia małżeństw w którym, dla pewnych zbiorów dziewcząt i chłopców, 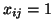$x_{ij}=1$ oznacza skojarzenie 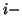$i-$tego chlopca z 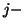$j-$tą dziewczyną w parę, zaś 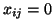$x_{ij}=0$ oznacza, że z 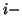$i-$tego chłopca i 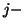$j-$tej dziewczyny pary nie będzie. I tym razem 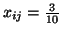$x_{ij}=\frac{3}{10}$ nie ma sensownej (ani przyzwoitej) interpretacji^8.2.