



Next: Funkcje zmiennej zespolonej
Up: Zadania z matematyki dla
Previous: Całki powierzchniowe
Contents
- Wykaż że jeśli
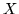 jest przestrzenią unormowaną
nad ciałem K, wtedy:
jest przestrzenią unormowaną
nad ciałem K, wtedy:
są funkcjami ciągłymi.
- Zbadaj zbieżność, bezwzględną zbieżność
i ew. obliczyć sumy szeregów:
- (a)
-
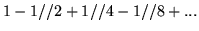
- (b)
-
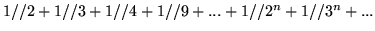
- (c)
-
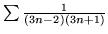
- (d)
-
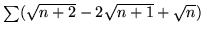
- Zbadaj zbieżność szeregów:
- (a)
-
![$0,001 + \sqrt{0,001} + \sqrt[3]{0,001} + ...$](img602.gif)
- (b)
-
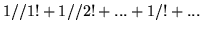
- (c)
-
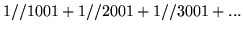
- (d)
-
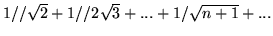
- (e)
-
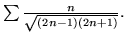
- Ile wyrazów szeregu
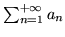 należy
zsumować, by
obliczyć jego sumę z dokładnością do
należy
zsumować, by
obliczyć jego sumę z dokładnością do 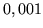 jeżeli:
jeżeli:
(a)
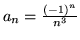 (b)
(b)
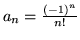
- Wykaż, że jeśli zbieżne są szeregi
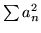 i
i
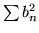 , wtedy także
szeregi
, wtedy także
szeregi
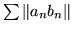 oraz
oraz
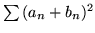 są zbieżne.
są zbieżne.
- Zbadaj zbieżność szeregów o wyrazie ogólnym:
(a) 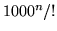 (b)
(b) 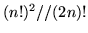 (c)
(c) 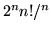
(d) 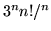 (e)
(e)
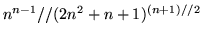
(f)
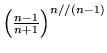 (g)
(g)
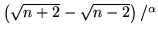 (h)
(h)
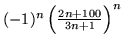
- Określ charakter zbieżności poniższych szeregów
funkcyjnych:
- (a)
-
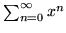 w przedziale (i)
w przedziale (i)
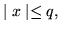
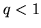 (ii)
(ii)
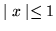 .
.
- (b)
-
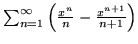
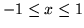
- (c)
-
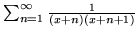
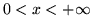
- Wykaż jednostajną zbieżność szeregów we
wskazanych zbiorach:
- (a)
-
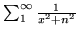
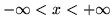
- (b)
-
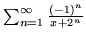
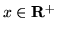
- (c)
-
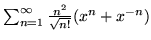
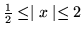
- (d)
-
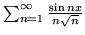
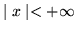
- Wykaż, że jeśli szereg
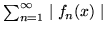 jest zbieżny jednostajnie w przedziale
jest zbieżny jednostajnie w przedziale 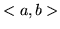 , to także szereg
, to także szereg
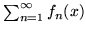 jest jednostajnie zbieżny w
jest jednostajnie zbieżny w 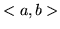 .
.
- (a)
- Wykaż, że ciąg
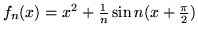 jest zbieżny
jednostajnie w
jest zbieżny
jednostajnie w 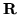 , a mimo to
, a mimo to
- (b)
- Wykaż, że ciąg
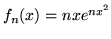 jest zbieżny
w
jest zbieżny
w 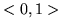 , lecz
, lecz
Skomentuj!
- Całkując w przedziale
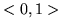 szereg
szereg
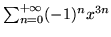 oblicz
oblicz
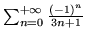 .
.
Podobnie, wykorzystaj rozwinięcie
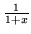 do obliczenia
do obliczenia
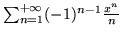 dla
dla 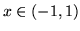 oraz
oraz
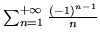 ,
,
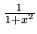 do obliczenia
do obliczenia
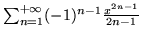 dla
dla 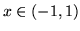 oraz
oraz
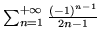 .
.
- Przedstaw w postaci szeregów całki niewłaściwe:
Ile wyrazów odpowiedniego szeregu należy zsumować, by otrzymać
wartość całki z dokładnością co najmniej 0,01 ?
- Zbadaj zbiór określoności i różniczkowalności
funkcji
 zdefiniowanej wzorem:
zdefiniowanej wzorem:
- Znajdź promień zbieżności szeregów
potęgowych
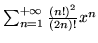
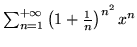
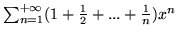
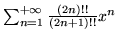
- Rozłóż w szereg Taylora funkcje:
(a) 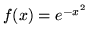 (
(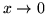 )
(b)
)
(b) 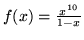 (
(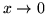 )
(c)
)
(c) 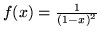 (
(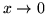 )
)




Next: Funkcje zmiennej zespolonej
Up: Zadania z matematyki dla
Previous: Całki powierzchniowe
Contents
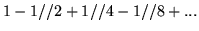
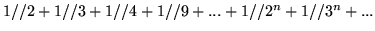
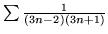
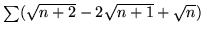
![$0,001 + \sqrt{0,001} + \sqrt[3]{0,001} + ...$](img602.gif)
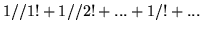
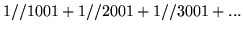
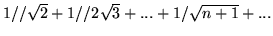
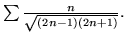
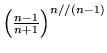 (g)
(g)
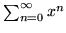 w przedziale (i)
w przedziale (i)
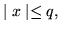
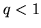 (ii)
(ii)
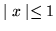 .
.
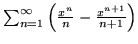
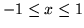
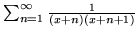
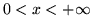
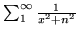
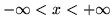
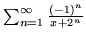
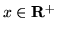
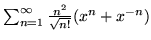
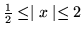
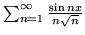
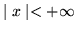
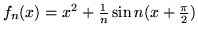 jest zbieżny
jednostajnie w
jest zbieżny
jednostajnie w 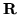 , a mimo to
, a mimo to
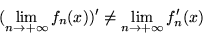
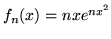 jest zbieżny
w
jest zbieżny
w 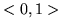 , lecz
, lecz
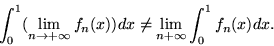
![]() do obliczenia
do obliczenia
![]() dla
dla ![]() oraz
oraz
![]() ,
,
![]() do obliczenia
do obliczenia
![]() dla
dla ![]() oraz
oraz
![]() .
.
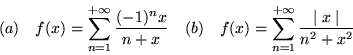
(
) (b)
(
) (c)
(
)