



Next: Szeregi
Up: Zadania z matematyki dla
Previous: Całki wielokrotne, krzywoliniowe i
Contents
- Oblicz całki powierzchniowe niezorientowane:
- (a)
-
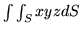 , gdzie
, gdzie  jest wycinkiem kuli
jest wycinkiem kuli
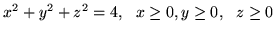 .
.
- (b)
-
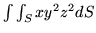 , gdzie
, gdzie  jest cęścią stożka
jest cęścią stożka
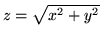 położoną nad podzbiorem płaszczyzny
położoną nad podzbiorem płaszczyzny 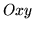 ograniczonym nierównościami:
ograniczonym nierównościami:
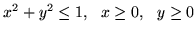 .
.
- (c)
-
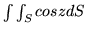 , gdzie
, gdzie  jest wycinkiem płaszczyzny
jest wycinkiem płaszczyzny
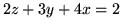 której rzutem na płaszczyzne
której rzutem na płaszczyzne 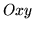 jest
jest
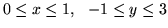 .
.
- (d)
-
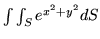 , gdzie
, gdzie  jet częścią stożka
jet częścią stożka
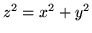 ponad kołem
ponad kołem
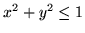 dla
dla 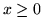 i
i 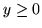 .
.
- (e)
-
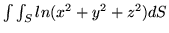 , gdzie
, gdzie  jest częścią sfery
jest częścią sfery
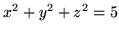 ponad kołem
ponad kołem
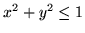 .
.
- (f)
-
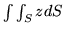 , gdzie
, gdzie  jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i
jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i 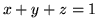 .
.
- (g)
-
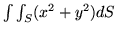 , gdzie
, gdzie  jest powierzchnią ograniczoną
zamkniętym walcem:
jest powierzchnią ograniczoną
zamkniętym walcem: 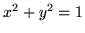 ,
,
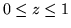 .
.
- Oblicz strumień cieczy przepływającej ku górze przez
północną sferę
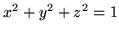 przy szybkości przepływu
przy szybkości przepływu
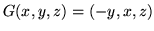 .
.
-
Oblicz całki powierzchniowe zorientowane wiedząc, że w każdym
z przykładów powierzchnia
 jest zorientowana ku górze:
jest zorientowana ku górze:
- (a)
-
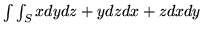 , gdy
, gdy
- (i)
 jest zadane przez:
jest zadane przez:
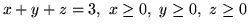 ,
,
- (ii)
 jest zadane przez:
jest zadane przez:
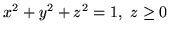 .
.
- (b)
-
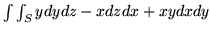 , gdy
, gdy  jest zadana przez:
jest zadana przez:
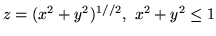
-
Znajdź strumień wypływający na zewnątrz powierzchni zamkniętej
 gdy
gdy
- (a)
 jest czworościanem ograniczonym przez płaszczyznę
jest czworościanem ograniczonym przez płaszczyznę
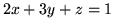 i płaszczyznami układu współrzędnych a prędkość
przepływu
i płaszczyznami układu współrzędnych a prędkość
przepływu
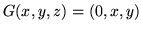 .
.
- (b)
 jest ograniczona przez stożek
jest ograniczona przez stożek
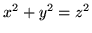 i płaszczyznę
i płaszczyznę 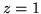
a prędkość przepływu
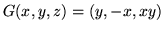 .
.
- Korzystając z twierdzenia Gaussa-Ostrogradzkiego oblicz te z całek zadań
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) i
i ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) w których
w których  jest powierzchnią zamkniętą.
jest powierzchnią zamkniętą.
- Oblicz strumień cieczy wypływający na zawnątrz powierzchni
 z
prędkością
z
prędkością 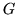 .
.
- (a)
-
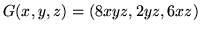 ,
,
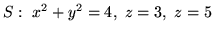
- (b)
-
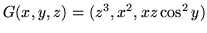 ,
, 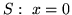 ,
,
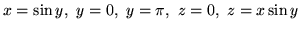 .
.
- (c)
-
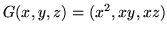 ,
,
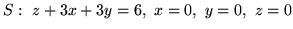 .
.
- Poniższe całki oblicz
- (a)
- korzystając ze wzoru na zamianę całki krzywoliniowej na oznaczoną (bez
korzystania z twierdzenia Stokesa),
- (b)
- korzystając z twierdzenia Stokesa.
(W każdym z przykładów wybierz jednż z dwóch możliwych orientacji
krzywej 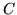 .)
.)
- (i)
-
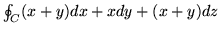 ,
,
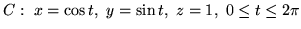
- (ii)
-
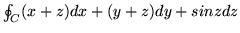 ,
,
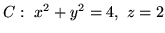
- Korzystając z twierdzenia Stokesa oblicz (
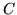 zorientuj jakkolwiek):
zorientuj jakkolwiek):
- (a)
-
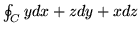 ,
, 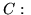 trójkąt o wierzchołkach
trójkąt o wierzchołkach
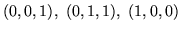 .
.
- (b)
-
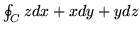 , gdzie
, gdzie 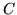 jest przecięciem powierzchni o równaniu
jest przecięciem powierzchni o równaniu
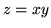 z walcem
z walcem 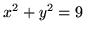 .
.
- (c)
-
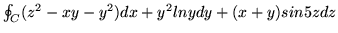 , gdzie
, gdzie 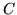 jest
przecięciem płaszczyzny
jest
przecięciem płaszczyzny 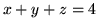 z płaszczyznami układu.
z płaszczyznami układu.




Next: Szeregi
Up: Zadania z matematyki dla
Previous: Całki wielokrotne, krzywoliniowe i
Contents
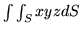 , gdzie
, gdzie  jest wycinkiem kuli
jest wycinkiem kuli
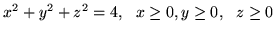 .
.
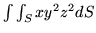 , gdzie
, gdzie  jest cęścią stożka
jest cęścią stożka
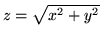 położoną nad podzbiorem płaszczyzny
położoną nad podzbiorem płaszczyzny 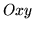 ograniczonym nierównościami:
ograniczonym nierównościami: 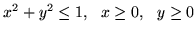 .
.
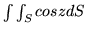 , gdzie
, gdzie  jest wycinkiem płaszczyzny
jest wycinkiem płaszczyzny
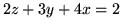 której rzutem na płaszczyzne
której rzutem na płaszczyzne 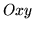 jest
jest
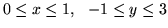 .
.
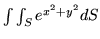 , gdzie
, gdzie  jet częścią stożka
jet częścią stożka
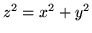 ponad kołem
ponad kołem 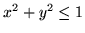 dla
dla 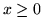 i
i 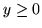 .
.
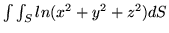 , gdzie
, gdzie  jest częścią sfery
jest częścią sfery
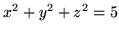 ponad kołem
ponad kołem
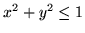 .
.
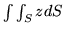 , gdzie
, gdzie  jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i
jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i 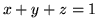 .
.
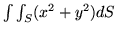 , gdzie
, gdzie  jest powierzchnią ograniczoną
zamkniętym walcem:
jest powierzchnią ograniczoną
zamkniętym walcem: 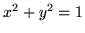 ,
,
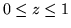 .
.
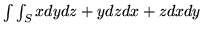 , gdy
, gdy
 jest zadane przez:
jest zadane przez:
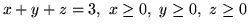 ,
,
 jest zadane przez:
jest zadane przez:
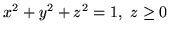 .
.
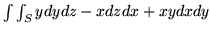 , gdy
, gdy  jest zadana przez:
jest zadana przez:
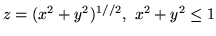
 jest czworościanem ograniczonym przez płaszczyznę
jest czworościanem ograniczonym przez płaszczyznę
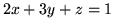 i płaszczyznami układu współrzędnych a prędkość
przepływu
i płaszczyznami układu współrzędnych a prędkość
przepływu
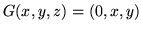 .
.
 jest ograniczona przez stożek
jest ograniczona przez stożek
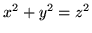 i płaszczyznę
i płaszczyznę 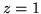
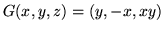 .
.
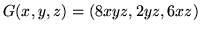 ,
,
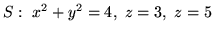
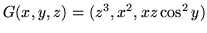 ,
, 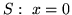 ,
,
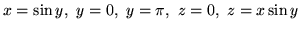 .
.
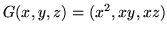 ,
,
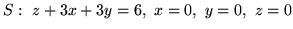 .
.
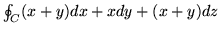 ,
,
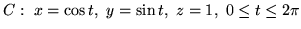
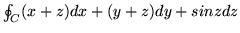 ,
,
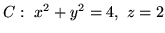
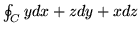 ,
, 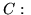 trójkąt o wierzchołkach
trójkąt o wierzchołkach
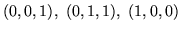 .
.
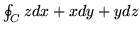 , gdzie
, gdzie 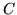 jest przecięciem powierzchni o równaniu
jest przecięciem powierzchni o równaniu
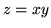 z walcem
z walcem 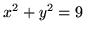 .
.
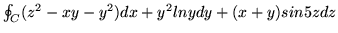 , gdzie
, gdzie 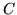 jest
przecięciem płaszczyzny
jest
przecięciem płaszczyzny 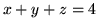 z płaszczyznami układu.
z płaszczyznami układu.