



Next: Równania różniczkowe
Up: Zadania z matematyki dla
Previous: Szeregi
Contents
- Dwiema metodami oblicz pochodną funkcji
 jeśli
jeśli
a) 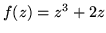 b)
b)
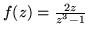
- Wykaż, że
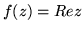 nie ma pochodnej w żadnym punkcie płaszczyzny.
nie ma pochodnej w żadnym punkcie płaszczyzny.
- Sprawdź, czy funkcja
(a)
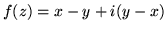
(b)
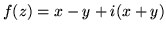
jest różniczkowalna?
- Oblicz promień zbieżności szeregu
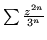 . W
obliczeniach wykorzystywany jest wzór
. W
obliczeniach wykorzystywany jest wzór
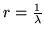 ,
gdzie
,
gdzie
![$\lambda = \lim sup{\sqrt[n]{\mid a_n \mid }}$](img672.gif) .
Wskaż, w którym miejscu rozumowania interweniuje fakt, że w
definicji
.
Wskaż, w którym miejscu rozumowania interweniuje fakt, że w
definicji 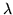 występuje granica górna, a nie zwykła
granica ciągu?
występuje granica górna, a nie zwykła
granica ciągu?
- Który z szeregów:
definiuje funkcję całkowitą?
- Znajdź funkcję holomorficzną
 , taką że
, taką że
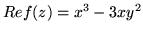 dwiema
metodami:
dwiema
metodami:
a) odgadując jedyne możliwe rozwiązanie
b) korzystając z odpowiedniego wzoru.
- Wykaż, że
(a) funkcje 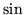 i
i 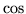 nie są ograniczone w
nie są ograniczone w 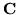
(b) 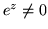 dla każdego
dla każdego 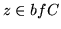
(c)
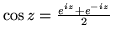
Z tego ostatniego wzoru wywnioskuj o okresowości funkcji 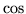 i
i 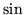 , wzory redukcyjne (formalnie identyczne z wzorami
redukcyjnymi rzeczywistych funkcji
, wzory redukcyjne (formalnie identyczne z wzorami
redukcyjnymi rzeczywistych funkcji 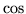 i
i 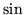 , wzory na
kosinus i sinus sumi oraz
, wzory na
kosinus i sinus sumi oraz
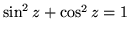 (dla
(dla
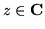 .
.
- Oblicz całki:
a)
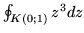 b)
b)
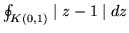
c)
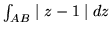 oraz
oraz
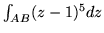 po odcinku
łączącym
po odcinku
łączącym 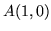 z
z 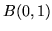
d)
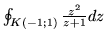
e)
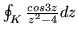 gdzie
gdzie
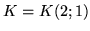 ,
, 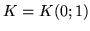 ,
,
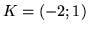 .
.




Next: Równania różniczkowe
Up: Zadania z matematyki dla
Previous: Szeregi
Contents